条件式と位置ベクトル

こんにちは、リンス(@Lins016)です。
今回は条件式と位置ベクトルについて学習していこう。

条件式は始点をそろえて位置ベクトルを表そう

ベクトルの条件式は必ず始点をそろえた形に変形しよう。

平面ベクトルは基準のベクトルを二つ決めて、その他のベクトルも\(\small{ \ \overrightarrow{ \mathrm{MN} }=s \overrightarrow{ \mathrm{AB} }+t \overrightarrow{ \mathrm{AC} } \ }\)のような基準のベクトルの実数倍の和（差）の形にするのが基本だから条件式もこの形に変形しよう。

\(\small{ \ 0 \ }\)じゃなくて\(\small{ \ \overrightarrow{ 0 } \ }\)零ベクトルに注意しよう

位置ベクトルの条件式では
\(\small{ \ a\overrightarrow{ \mathrm{AP} }+b \overrightarrow{ \mathrm{BP} }+c \overrightarrow{ \mathrm{CP} }= \overrightarrow{ 0 } \ }\)
のように右辺は\(\small{ \ 0 \ }\)じゃなくて\(\small{ \ \overrightarrow{ 0 } \ }\)になるから注意しよう。

ベクトルは大きさと向きを定めたもので、数は大きさだけしか持たないからベクトルじゃない。この大きさだけ定めたものをベクトルに対してスカラーっていうから言葉だけでも知っておこう。

つまり\(\small{ \ a\overrightarrow{ \mathrm{AP} }+b \overrightarrow{ \mathrm{BP} }+c \overrightarrow{ \mathrm{CP} }=0 \ }\)
とすると左辺はベクトル、右辺はスカラーってことになって等しくならないんだ。

問題文を書き写すときに\(\small{ \ \overrightarrow{ 0 } \ }\)を\(\small{ \ 0 \ }\)って書き間違えないように注意しよう。

\(\small{ \ \overrightarrow{ 0 } \ }\)のことを零ベクトルっていって、大きさ\(\small{ \ ０ \ }\)の向きも考えないベクトルのことなんだ。

三角形ABCと点Pの位置ベクトルの条件式

\(\small{ \ a\overrightarrow{ \mathrm{AP} }+b \overrightarrow{ \mathrm{BP} }+c \overrightarrow{ \mathrm{CP} }= \overrightarrow{ 0 } \ }\)
のような\(\small{ \ \triangle \mathrm{ABC} \ }\)と点\(\small{ \ \mathrm{P} \ }\)との条件式から位置ベクトルを求める問題について考えてみよう。

この問題では\(\small{ \ \triangle \mathrm{ABC} \ }\)に対して点\(\small{ \ \mathrm{P} \ }\)がどこにあるかを表せばいいから、点\(\small{ \ \mathrm{A} \ }\)を始点にして、\(\small{ \ \overrightarrow{ \mathrm{AB} } \ }\)と\(\small{ \ \overrightarrow{ \mathrm{AC} } \ }\)の二つの基準のベクトルで\(\small{ \ \overrightarrow{ \mathrm{AP} } \ }\)を表そう。

このとき\(\small{ \ \overrightarrow{ \mathrm{BP} }= \overrightarrow{ \mathrm{AP} }- \overrightarrow{ \mathrm{AB} } \ }\)の変形を利用してすべてのベクトルを始点\(\small{ \ \mathrm{A} \ }\)から始めるようにしよう。

また「問題文が点\(\small{ \ \mathrm{P} \ }\)の位置を答えよ」って問題の場合、\(\small{ \ \overrightarrow{ \mathrm{AP} }= s\overrightarrow{ \mathrm{AB} }+t\overrightarrow{ \mathrm{AC} } \ }\)の形に変形しただけじゃ答えになっていないんだ。

だから点\(\small{ \ \mathrm{P} \ }\)と\(\small{ \ \triangle \mathrm{ABC} \ }\)の位置関係をきちんと答えないといけない。

つまり「点\(\small{ \ \mathrm{P} \ }\)は\(\small{ \ \mathrm{BC} \ }\)を○：△に内分する点を\(\small{ \ \mathrm{Q} \ }\)とすると\(\small{ \ \mathrm{AQ} \ }\)を○：○に内分する点」っていう答え方をしないといけない。

そのためには直線\(\small{ \ \mathrm{AP} \ }\)と直線\(\small{ \ \mathrm{BC} \ }\)の交点\(\small{ \ \mathrm{Q} \ }\)の位置を求める必要がある。

\(\small{ \ \overrightarrow{ \mathrm{AP} }=\displaystyle \frac{1}{3} \overrightarrow{ \mathrm{AB} }+\displaystyle \frac{2}{5} \overrightarrow{ \mathrm{AC} }}\)を例に変形の仕方を覚えておこう。

\(\small{\begin{eqnarray} \ \overrightarrow{ \mathrm{AP} }&=&\displaystyle \frac{1}{3} \overrightarrow{ \mathrm{AB} }+\displaystyle \frac{2}{5} \overrightarrow{ \mathrm{AC} }\\
&=&\displaystyle \frac{5}{15} \overrightarrow{ \mathrm{AB} }+\displaystyle \frac{6}{15} \overrightarrow{ \mathrm{AC} }\cdots①\\
&=& \displaystyle \frac{5+6}{15}\times \displaystyle \frac{5 \overrightarrow{ \mathrm{AB} }+6 \overrightarrow{ \mathrm{AC} }}{5+6}\cdots②\\
&=& \displaystyle \frac{11}{15}\times \displaystyle \frac{5 \overrightarrow{ \mathrm{AB} }+6 \overrightarrow{ \mathrm{AC} }}{11}\\
&=& \displaystyle \frac{11}{15}\overrightarrow{ \mathrm{AQ} } \end{eqnarray}}\)

\(\small{ ① }\)で係数を通分して\(\small{ ② }\)で通分した分母を前に出して、\(\small{ ① }\)の分子を足した値を前の項の分子と後ろの項の分母に書き加えるんだ。

\(\small{\displaystyle \frac{5}{11} \overrightarrow{ \mathrm{AB} }+\displaystyle \frac{6}{11} \overrightarrow{ \mathrm{AC} } \ }\)の係数は足したら\(\small{ \ 1 \ }\)になるから直線\(\small{ \ \mathrm{BC} \ }\)上にあることがいえるよね。

つまり\(\small{ \displaystyle \frac{5 \overrightarrow{ \mathrm{AB} }+6 \overrightarrow{ \mathrm{AC} }}{11} \ }\)が\(\small{ \ \mathrm{BC} \ }\)を\(\small{ \ 6:5 \ }\)に内分する点の位置ベクトルになるんだ。

問題解答

\(\small{ \ \triangle \mathrm{ABC} \ }\)と点\(\small{ \ \mathrm{P} \ }\)に対して、等式\(\small{ \ 6 \overrightarrow{ \mathrm{AP} }+3 \overrightarrow{ \mathrm{BP} }+2 \overrightarrow{ \mathrm{CP} }= \overrightarrow{ 0 } \ }\)が成り立つとき、点\(\small{ \ \mathrm{P} \ }\)はどのような位置にあるか。

\(\small{ \ 6 \overrightarrow{ \mathrm{AP} }+3 \overrightarrow{ \mathrm{BP} }+2 \overrightarrow{ \mathrm{CP} }= \overrightarrow{ 0 } \ }\)
\(\small{ \ 6 \overrightarrow{ \mathrm{AP} }+3\left( \overrightarrow{ \mathrm{AP} }- \overrightarrow{ \mathrm{AB} }\right)+2\left( \overrightarrow{ \mathrm{AP} }- \overrightarrow{ \mathrm{AC} }\right)= \overrightarrow{ 0 } \ }\)

\(\small{ \ 11\overrightarrow{ \mathrm{AP} }=3 \overrightarrow{ \mathrm{AB} }+2 \overrightarrow{ \mathrm{AC} } \ }\)
\(\small{\begin{eqnarray} \ \overrightarrow{ \mathrm{AP} }&=&\displaystyle \frac{3}{11} \overrightarrow{ \mathrm{AB} }+\displaystyle \frac{2}{11} \overrightarrow{ \mathrm{AC} }\\
&=& \displaystyle \frac{5}{11}\times \displaystyle \frac{3 \overrightarrow{ \mathrm{AB} }+2 \overrightarrow{ \mathrm{AC} }}{5}\\
&=&\displaystyle \frac{5}{11}\times \displaystyle \frac{3 \overrightarrow{ \mathrm{AB} }+2 \overrightarrow{ \mathrm{AC} }}{2+3} \ \end{eqnarray}}\)

よって辺\(\small{ \ \mathrm{BC} \ }\)を\(\small{ \ 2:3 \ }\)に内分する点を\(\small{ \ \mathrm{D} \ }\)とすると、点\(\small{ \ \mathrm{P} \ }\)は線分\(\small{ \ \mathrm{AD} \ }\)を\(\small{ \ 5:6 \ }\)に内分する点

今回は問題にないけど、線分比が求まると\(\small{ \ \triangle \mathrm{ABP} \ }\)と\(\small{ \ \triangle \mathrm{ACP} \ }\)と\(\small{ \ \triangle \mathrm{BCP} \ }\)の面積比も求まるからチェックしておこう。
\(\small{ \ \triangle \mathrm{ABC} \ }\)の面積を\(\small{ \ \mathrm{S} \ }\)として計算してみよう。

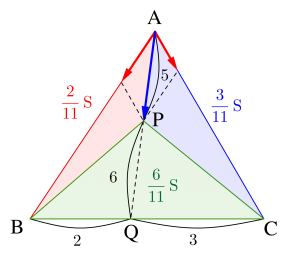
三角形ABCと外心Oの位置ベクトルの条件式

次に\(\small{ \ a \overrightarrow{ \mathrm{OA} }+b \overrightarrow{ \mathrm{OB} }+c \overrightarrow{ \mathrm{OC} }= \overrightarrow{ 0 } \ }\)
のような外心\(\small{ \ \mathrm{O} \ }\)と\(\small{ \ \triangle \mathrm{ABC} \ }\)の条件式から面積や辺の長さを求める問題について考えていこう。

この問題では\(\small{ \ \overrightarrow{ \mathrm{OA} } \ }\)、\(\small{ \ \overrightarrow{ \mathrm{OB} } \ }\)、\(\small{ \ \overrightarrow{ \mathrm{OC} } \ }\)の三つのベクトルが与えられているから、まずは一つのベクトルを残りの二つのベクトルで表そう。

つまり\(\small{ \ \overrightarrow{ \mathrm{OC} }=s \overrightarrow{ \mathrm{OA} }+t \overrightarrow{ \mathrm{OB} } \ }\)の形に変形して、\(\small{ \ \overrightarrow{ \mathrm{OA} } \ }\)と\(\small{ \ \overrightarrow{ \mathrm{OB} } \ }\)を基準のベクトルにして\(\small{ \ \overrightarrow{ \mathrm{OC} } \ }\)を表そう。

さらに点\(\small{ \ \mathrm{O} \ }\)は外心だから\(\small{ \ \left| \overrightarrow{ \mathrm{OA} }\right|=\left| \overrightarrow{ \mathrm{OB} }\right|=\left| \overrightarrow{ \mathrm{OC} }\right| \ }\)が言える。

この式と\(\small{ \ \overrightarrow{ \mathrm{OC} }=s \overrightarrow{ \mathrm{OA} }+t \overrightarrow{ \mathrm{OB} } \ }\)から内積\(\small{ \ \overrightarrow{ \mathrm{OA} }\cdot \overrightarrow{ \mathrm{OB} } \ }\)を求めよう。

そうすることで他の辺の長さや面積を求めることができるんだ。

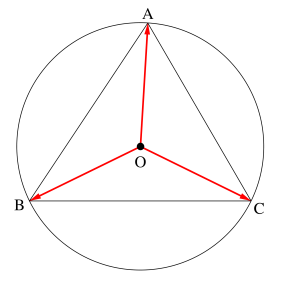
それじゃ例題で解き方を確認しておこう。

Point 条件式と位置ベクトル

①始点をそろえた基準のベクトルを定めよう
②すべてのベクトルを始点から始まるベクトルに変換しよう