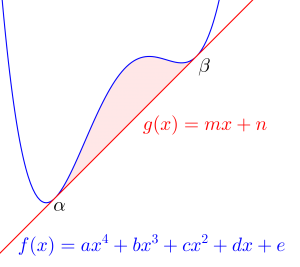こんにちは、リンス(@Lins016)です。
今回は第一種オイラー積分(ベータ関数)の証明とその利用について学習していこう。
第一種オイラー積分・ベータ関数
第一種オイラー積分と呼ばれる積分の式を部分積分を利用して証明していこう。
この関数はベータ関数とも言って大学で学習する範囲になるんだけど、部分積分を利用することでこの関数を証明することが出来るんだ。
ちなみにこの証明がそのまま入試問題として出題されることもあるからね。
さらにこの第一種オイラー積分を利用することで数学Ⅱで利用する積分の面積の公式も導くことが出来るから、それも合わせて学習しておこう。
\(\small{ \ p=1, \ q=1 \ }\)のとき
\(\small{ \ p=1, \ q=2 \ }\)のとき
\(\small{ \ p=2, \ q=2 \ }\)のとき
第一種オイラー積分の証明
を証明してみよう。
\(\small{ \ I_{p, \ q}=\displaystyle\int_{\alpha}^{\beta}\left(x-\alpha\right)^p\left(\beta-x\right)^q dx \ }\)として部分積分を利用すると
I_{p, \ q}&=&\displaystyle\int_{\alpha}^{\beta}\left(x-\alpha\right)^p\left(\beta-x\right)^q dx\\
&=&\displaystyle\int_{\alpha}^{\beta}\left\{\displaystyle\frac{1}{p+1}\left(x-\alpha\right)^{p+1}\right\}'\left(\beta-x\right)^q dx\\
&=&\left[\displaystyle\frac{1}{p+1}\left(x-\alpha\right)^{p+1}\left(\beta- x\right)^q \right]_{\alpha}^{\beta}-\displaystyle\int_{\alpha}^{\beta}\displaystyle\frac{1}{p+1}\left(x-\alpha\right)^{p+1}\left\{\left(\beta-x\right)^q\right\}dx\\
&=&\displaystyle\int_{\alpha}^{\beta}\displaystyle\frac{1}{p+1}\left(x-\alpha\right)^{p+1}q\cdot \left(\beta-x\right)^{q-1}(-1)dx\\
&=&\displaystyle\frac{q}{p+1}\displaystyle\int_{\alpha}^{\beta}\left(x-\alpha\right)^{p+1} \left(\beta-x\right)^{q-1}dx\\
&=&\displaystyle\frac{q}{p+1}I_{p+1, \ q-1}
\ \end{eqnarray}}\)
\(\small{ \ I_{p, \ q}=\displaystyle\frac{q}{p+1}I_{p+1, \ q-1} \ }\)より
&=&\displaystyle\frac{q}{p+1}\cdot\displaystyle\frac{q-1}{p+2}I_{p+2, \ q-2}\\
&=&\displaystyle\frac{q}{p+1}\cdot\displaystyle\frac{q-1}{p+2}\cdot\displaystyle\frac{q-2}{p+3}I_{p+3, \ q-3}\\
&=&\displaystyle\frac{q}{p+1}\cdot\displaystyle\frac{q-1}{p+2}\cdot\displaystyle\frac{q-2}{p+3}\cdot\cdots\cdot\displaystyle\frac{2}{p+q-1}\cdot\displaystyle\frac{1}{p+q}I_{p+q, \ 0}
\ \end{eqnarray}}\)
\(\small{\begin{eqnarray} \ I_{p+q, \ 0}&=&\displaystyle\int_{\alpha}^{\beta}\left(x-\alpha\right)^{p+q}\left(\beta-x\right)^0 dx\\
&=&\displaystyle\int_{\alpha}^{\beta}\left(x-\alpha\right)^{p+q}dx\\
&=&\left[\displaystyle\frac{1}{p+q+1}\left(x-\alpha\right)^{p+q+1}\right]_{\alpha}^{\beta}\\
&=&\displaystyle\frac{1}{p+q+1}\left(\beta-\alpha\right)^{p+q+1} \ \end{eqnarray}}\)
&=&\displaystyle\frac{q}{p+1}\cdot\displaystyle\frac{q-1}{p+2}\cdot\displaystyle\frac{q-2}{p+3}\cdot\cdots\cdot\displaystyle\frac{2}{p+q-1}\cdot\displaystyle\frac{1}{p+q}\cdot\displaystyle\frac{1}{p+q+1}\left(\beta-\alpha\right)^{p+q+1}
\ \end{eqnarray}}\)
分母分子にそれぞれ\(\small{ \ p! \ }\)をかけると
面積の公式への応用
この第一種オイラー積分を利用することで数学Ⅱの積分法の面積の公式に応用することができるんだ。
①\(\small{ \ p=1, \ q=1 \ }\)のとき
\(\small{ \ \displaystyle\int_{\alpha}^{\beta}\left(x-\alpha\right)\left(x-\beta\right) dx=-\displaystyle\frac{1}{6}\left(\beta-\alpha\right)^3 \ }\)
これは放物線と直線、または放物線と放物線の二本の線で囲まれた面積を求めるときに使える式になるよね。
\(\small{\begin{eqnarray} \ S&=&\displaystyle\int_{\alpha}^{\beta}\left\{g(x)-f(x)\right\}dx\\
&=&-a\displaystyle\int_{\alpha}^{\beta}\left(x-\alpha\right)\left(x-\beta\right) dx\\
&=&\displaystyle\frac{a}{6}\left(\beta-\alpha\right)^3 \ \end{eqnarray}}\)
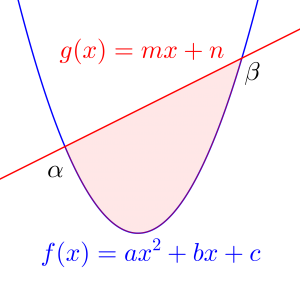
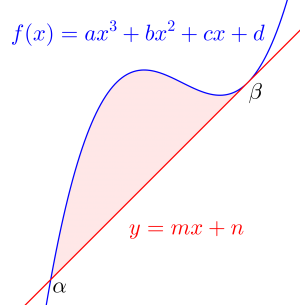
②\(\small{ \ p=1, \ q=2 \ }\)のとき
\(\small{ \ \displaystyle\int_{\alpha}^{\beta}\left(x-\alpha\right)\left(x-\beta\right)^2 dx=-\displaystyle\frac{1}{12}\left(\beta-\alpha\right)^4 \ }\)
これは三次関数と接線に囲まれた面積を求めるときに使える式になるからね。
\(\small{\begin{eqnarray} \ S&=&\displaystyle\int_{\alpha}^{\beta}\left\{f(x)-g(x)\right\}dx\\
&=&a\displaystyle\int_{\alpha}^{\beta}\left(x-\alpha\right)\left(x-\beta\right)^2 dx\\
&=&\displaystyle\frac{a}{12}\left(\beta-\alpha\right)^4 \ \end{eqnarray}}\)
③\(\small{ \ p=2, \ q=2 \ }\)のとき
\(\small{ \ \displaystyle\int_{\alpha}^{\beta}\left(x-\alpha\right)^2\left(x-\beta\right)^2 dx=\displaystyle\frac{1}{30}\left(\beta-\alpha\right)^5 \ }\)
これは四次関数と重接線に囲まれた面積を求めるときに使える式になるからね。
\(\small{\begin{eqnarray} \ S&=&\displaystyle\int_{\alpha}^{\beta}\left\{f(x)-g(x)\right\}dx\\
&=&a\displaystyle\int_{\alpha}^{\beta}\left(x-\alpha\right)^2\left(x-\beta\right)^2 dx\\
&=&\displaystyle\frac{a}{30}\left(\beta-\alpha\right)^5 \ \end{eqnarray}}\)