こんにちは、リンス(@Lins016)です。
今回はデータの代表値について学習していこう。
データの代表値(平均値・中央値・最頻値)
データの分析する上で覚えておきたい値っていうのがある。それが代表値って呼ばれる値なんだ。
代表値にはいろんな値があるけど、今回は、その中の平均値と中央値と最頻値について学習していこう。
そして、その代表値はどうやって求めるのか、さらにそれぞれの代表値のメリットやデメリットについても考えてみよう。
平均値・・・データの総和をデータの個数で割った値
中央値・・・データを大きさ順に並べたとき中央にある値
最頻値・・・最も多い個数の値
平均値とは
平均値とは、変量\(\small{ \ x \ }\)のデータの値の総和をデータの個数で割った値のこと。
テストの平均点とか、生活の中で使うことも多いよね。
一般的に、\(\small{ \ x \ }\)の平均を\(\small{ \ \overline{x} \ }\)って書くから覚えておこう。
ちなみに平均には相加平均や相乗平均、調和平均とか、いろんな平均がある。
「データの分析」で利用する平均値は、相加平均のことだからね。
その他の平均については、また今度解説するね。
また、度数分布表から平均値を求める場合は、すべての「階級値×その階級のデータの個数」の和をすべてのデータの個数で割って求めよう。
中央値(メジアン)とは
中央値とは、データを値の大きさの順に並べたとき、中央の位置にくる値のこと。
ただし、データの個数が偶数個の場合は、中央に2つの値が並ぶから、この2つの値の平均値が中央値ってことになるからね。
また、度数分布表から中央値を求める場合は、累計度数表を用いて求める方法や累計度数グラフを用いて求める方法などいくつかの方法がある。
だけど、求め方によって答えも少し異なるから、あまり出題されることはないと思う。
「例題を確認(\(\small{ \ 2 \ }\))」で累計度数表を用いて求める方法を掲載しているから確認しておこう。
最頻値(モード)とは
最頻値とは、データにおいて最も個数の多い値のこと。
度数分布表から最頻値を求める場合は、データの一番多い階級の階級値が最頻値になるからね。
各代表値のメリット・デメリット
平均値は全てのデータの値を利用するというメリットがある。でも、その一方ですべてのデータを利用するから、極端な値が含まれていると大きな影響を受けるというデメリットもあるよね。
中央値は中央の値だけ利用するから、極端な値の影響を受けないというメリットがある。でも、データの一部しか利用しないから、データ全体を確認することができないってデメリットもあるからね。
最頻値も極端な値の影響を受けないというメリットがあるけど、データの個数が少ない場合は、あまり意味がないよね。だって、もっとたくさんのデータを集めれば、最頻値が変わるかもしれないもんね。
次のデータは、ある学校の図書室が貸し出した本の冊数を\(\small{ \ 1 \ }\)ヵ月ごとに半年間記録したものである。
\(\small{230}\)、\(\small{320}\)、\(\small{200}\)、\(\small{240}\)、\(\small{120}\)、\(\small{270}\) (単位は冊)
(1)中央値と平均値を求めよ。
(2)上記の\(\small{ \ 6 \ }\)個の数値のうち\(\small{ \ 1 \ }\)個誤りであることがわかった。正しい数値に基づく中央値と平均値は、それぞれ\(\small{ \ 255 \ }\)冊と\(\small{ \ 240 \ }\)冊であるという。誤っている数値を選び、正しい数値を求めよ。
(1)データを小さい順に並べると
\(\small{ 120}\)、\(\small{200}\)、\(\small{230}\)、\(\small{240}\)、\(\small{270}\)、\(\small{320}\)
中央値\(\small{ \ M_e=\displaystyle \frac{230+240}{2}=235 \ }\)
(2)正しいデータのとき、データの総和は\(\small{ \ 240\times6=1440 \ }\)
誤っているデータのとき、データの総和は\(\small{ \ 230\times6=1380 \ }\)
よって正しいデータは誤っているデータより\(\small{ \ 60 \ }\)冊大きい
中央値が\(\small{ \ 255 \ }\)冊になればよいので、中央の\(\small{ \ 2 \ }\)つの数の和は\(\small{ \ 510 \ }\)冊になる
これを満たすのは\(\small{ \ 230 \ }\)冊のデータが\(\small{ \ 290 \ }\)冊のときだけ
よって誤ったデータは\(\small{ \ 230 \ }\)冊で、正しい値は\(\small{ \ 290 \ }\)冊である

ただし、並べ替えるとき書き写すミスしないようにね。
Point
①データは大きさの順に並べる。
②各代表値の性質(メリット・デメリット)を確認する。
次のデータは、ある学校の生徒\(\small{ \ 46 \ }\)人の握力の記録をまとめたものである。次の問いに答えよ。
\hline
階級(\mathrm{kg}) & 階級値(\mathrm{kg}) & 度数(人) & 階級値\times度数 \\
\hline
20-25 & 22.5 & 7 & 157.5 \\
\hline
25-30 & 27.5 & 8 & 220.0 \\
\hline
30-35 & ア & 14 & イ \\
\hline
35-40 & 37.5 & 13 & 487.5 \\
\hline
40-45 & 42.5 & 4 & 170.0 \\
\hline
計 & & 46 & ウ\\
\hline
\end{array}
\ }\)
(1)表のア~ウにあてはまる数を求めよ。
(2)この表から平均値を四捨五入によって、小数第\(\small{ \ 1 \ }\)位まで求めよ。
(3)累計度数表を作成し、累計度数表から中央値を求めよ。。ただし、四捨五入によって、小数第\(\small{ \ 1 \ }\)位まで求めよ。
度数分布表に累計度数も記入する
\hline
階級(\mathrm{kg}) & 階級値(\mathrm{kg}) & 度数(人) & 階級値\times度数&累計度数 \\
\hline
20-25 & 22.5 & 7 & 157.5 &7 \\
\hline
25-30 & 27.5 & 8 & 220.0 & 15\\
\hline
30-35 & ア & 14 & イ &29 \\
\hline
35-40 & 37.5 & 13 & 487.5 &42 \\
\hline
40-45 & 42.5 & 4 & 170.0 &46\\
\hline
計 & & 46 & ウ\\
\hline
\end{array}
\ }\)
(1)
ア\(\small{ \ \displaystyle\frac{30+35}{2}=32.5 \ }\)
イ\(\small{ \ 32.5\times14=455.0 \ }\)
(2)\(\small{ \ \overline{x}=\displaystyle\frac{1490.0}{46}=32.39 \ }\)
\(\small{ \ \therefore 32.4\mathrm{kg} \ }\)
(3)中央の生徒は\(\small{ \ 23 \ }\)番目と\(\small{ \ 24 \ }\)番目になり、これらの生徒は\(\small{ \ 30-35 \ }\)の階級にいることがわかる
\(\small{ \ 23 \ }\)番目の生徒の握力\(\small{ \ =30+5\times\displaystyle \frac{23-15}{14}=32.857 \ }\)
\(\small{ \ 24 \ }\)番目の生徒の握力\(\small{ \ =30+5\times\displaystyle \frac{24-15}{14}=33.214 \ }\)
\(\small{ \ M_e=\displaystyle \frac{32.857+33.214}{2}=33.0355 \ }\)
\(\small{ \ \therefore M_e=33.0 \ }\)

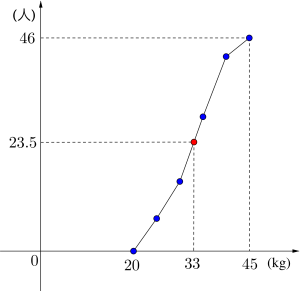
この問題では累計度数表を利用した中央値と全く同じ値になったけど、問題によっては少し異なる場合もあるからね。

