こんにちは、リンス(@Lins016)です。
今回は偏差値について学習していこう。
偏差値の仕組みを理解しよう
データの分析で学習した平均値や標準偏差を利用した値で代表的なものって、やっぱり偏差値だよね。
受験生は模試の結果で良く目にするよね。
でもどんな計算式かよくわからないで、模試の結果の偏差値を見て右往左往してる人っているから、偏差値をきちんと理解して、模試の結果を正しく分析しよう。
もちろん、数学Iのデータの分析でも出題されているから、偏差値を取り扱った問題を解くためにもしっかりと理解していこう。
偏差値 \(\small{ \ \mathrm{T}_i=\displaystyle \frac{x-\overline{x}}{s}\times10+50 \ }\)
\(\small{ \ x \ }\):テストの得点
\(\small{ \ \overline{x} \ }\):テストの平均点
\(\small{ \ s \ }\):テストの標準偏差
偏差値を利用するメリット
テストなどの複数教科の試験を受けた場合,平均点を同じにするのはかなり難しいよね。
つまり得点だけで各教科の実力の差を見極めることはできない。
だから偏差値を使うことで平均点が異なってても各教科の実力の差を比較しやすくなるんだ。
偏差値を用いることで自分の相対位置(大まかな順位)が調べることもできる。
ただ、それは得点分布が正規分布のような形になっている場合なんだ。
正規分布
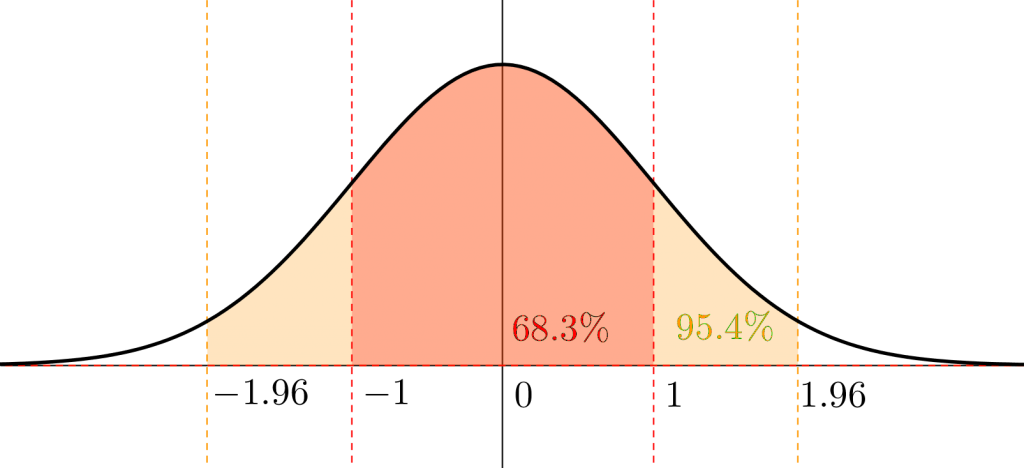
正規分布ってのは数学\(\small{ \ \mathrm{B} \ }\)の確率分布で学習するから、ここではあまり深くは学習しないけど、図のような分布を正規分布っていうんだ。
この分布は平均値付近(この図の場合は\(\small{ \ 0 \ }\))のデータが一番多く、釣鐘型の左右対称の分布で、\(\small{ \ -1\lt x \lt 1 \ }\)の間に\(\small{ \ 68.3 \ }\)%のデータが、\(\small{ \ -1.96\lt x \lt 1.96 \ }\)の範囲に\(\small{ \ 95.4 \ }\)%のデータが入っているような分布のことで、自然界でも正規分布の分布をとるものがあるぐらい有名な分布なんだ。
得点分布の標準化
得点の分布を次の計算式に入れることで偏差値を求めることができる。
得点の平均点を\(\small{ \ \overline{x} \ }\)、標準偏差を\(\small{ \ s \ }\)とすると
\(\small{ \ \displaystyle \frac{x-\overline{x}}{s}\times10+50 \ }\)
この式で得られる数値が偏差値になるんだ。
ただ、正規分布と異なるのは、平均点の偏差値が\(\small{ \ 0 \ }\)ではなく、\(\small{ \ 50 \ }\)になるってこと。
正規分布では\(\small{ \ -1\lt x \lt 1 \ }\)の間に\(\small{ \ 68.3 \ }\)%のデータが、\(\small{ \ -1.96\lt x \lt 1.96 \ }\)の範囲に\(\small{ \ 95.4 \ }\)%のデータが入っているような分布だった。
だけど、偏差値では\(\small{ \ 40\lt x\lt 60 \ }\)の間に\(\small{ \ 68.3 \ }\)%のデータが、\(\small{ \ 30\lt x\lt 70 \ }\)の範囲に\(\small{ \ 95.4 \ }\)%のデータが入っているような分布になる。
それは偏差を標準偏差で割ることで標準偏差\(\small{ \ 1 \ }\)の散らばりになって、さらにそれを\(\small{ \ 10 \ }\)倍してるから標準偏差\(\small{ \ 10 \ }\)の散らばりになる。
これに\(\small{ \ 50 \ }\)を加えることで、平均値を\(\small{ \ 50 \ }\)にしてるからなんだ。
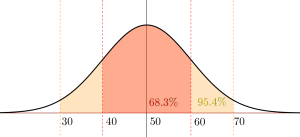
って言っても平均点付近の人数が一番多くて、\(\small{ \ 0 \ }\)点や\(\small{ \ 100 \ }\)点に近づくほど人数が少なくなる一般的なテストの場合だけ利用できるから、人数が少なすぎるテストとかだと、この分布の形にならないからあまり偏差値があてにならない。
たくさんの受験者がいるセンター試験や大手予備校が行っている全国規模の模試とかだと、この分布の形に近くなるから偏差値も有効になるんだ。
偏差値で求めることができる順位
一般に偏差値に対する上位からの割合(%)は
偏差値\(\small{ \ 70 \ }\)で上から\(\small{ \ 2.3 \ }\)%、偏差値\(\small{ \ 60 \ }\)で上から\(\small{ \ 15.9 \ }\)%、偏差値\(\small{ \ 50 \ }\)で上から\(\small{ \ 50 \ }\)%、偏差値\(\small{ \ 40 \ }\)で上から\(\small{ \ 84.1 \ }\)%、偏差値\(\small{ \ 30 \ }\)で上から\(\small{ \ 97.7 \ }\)%になるからこれを利用して大体の順位を確認することができる。
例えば\(\small{ \ 50 \ }\)万人が受験するセンター試験で、偏差値が\(\small{ \ 65 \ }\)なら得点分布が正規分布になると仮定すると、全国順位は大体\(\small{ \ 33,500 \ }\)位になるって言えるんだ。
偏差値のメリット・デメリット
偏差値を利用することで、種類の違う模試の結果も比較することができることになるよね。一般に大手予備校が実施している模試だと、前年のセンター試験等の結果を偏差値で比較して、大学合格の判定値を算出したりしているんだ。
だって点数が上がっても平均点も上がってたら、実際の順位が上がってるかどうかわからないもんね。
だから点数が上がったとかではなく偏差値がどう変化したっていう方がきちんと判定されることになるよね。
ただデメリットというか注意していて欲しいのは、医学部模試や東大などの大学別模試なんかだと受験層がセンター模試の分布の上位にいる生徒しか受けないから、センター模試の偏差値\(\small{ \ 50 \ }\)と大学別模試の偏差値\(\small{ \ 50 \ }\)は全然意味が違うことになるからね。
一般的な記述模試も同様だよ。だってセンター模試だと数学を受験するのは国立志望の生徒のほとんどになるけど、記述模試の数Ⅲ型を受験するのは理系の生徒だけになるから、受験者の層が全然違うことになるからね。
だからセンター模試の偏差値と記述模試や大学別模試なんかの偏差値は全く別だから注意するようにね。あくまで偏差値は合格基準の判定を出すために算出してるって考えておいた方がいいからね。受験層が異なる模試の偏差値を比較しても何にもならないから注意しよう。

簡単にいうと、例えば合格率\(\small{ \ 40 \ }\)%だと昨年度の受験で同じぐらいの点数でその大学を受験した生徒の約\(\small{ \ 10 \ }\)人に\(\small{ \ 4 \ }\)人が合格したってデータから\(\small{ \ 40 \ }\)%ってことになるんだ。
もちろん単純にそれだけで判定を出しているわけじゃなくて、複雑なデータの検証とかもあるからね。
だから大手予備校の判定システムによっては合格率が異なることも結構あるからね。
ある大学で\(\small{ \ 3n \ }\)人の学生がテストを受験し、そのうち\(\small{ \ 2n \ }\)人の学生が\(\small{ \ a \ }\)点、残りの\(\small{ \ n \ }\)人の学生が\(\small{ \ b \ }\)点だった。ただし、\(\small{ \ a\lt b \ }\)である。\(\small{ \ a \ }\)点を取った学生と\(\small{ \ b \ }\)点を取った学生の偏差値をそれぞれ求めよ。
ただし、偏差値は次の計算式で与えられる数値\(\small{ \ \mathrm{T} \ }\)である。
\(\small{ \ \mathrm{T}=\displaystyle \frac{x-\overline{x}}{s}\times10 +50 \ }\)
\(\small{ \ \overline{x} \ }\)は受験者の平均点、\(\small{ \ s \ }\)は受験生の得点の標準偏差である。
\(\small{ \ 3n \ }\)人の学生が受験し、\(\small{ \ a \ }\)点が\(\small{ \ 2n \ }\)人、\(\small{ \ b \ }\)点が\(\small{ \ n \ }\)人より平均点は
\(\small{ \ \overline{x}=\displaystyle \frac{a\times2n+b\times n}{3n}=\displaystyle \frac{2a+b}{3} \ }\)
このテストの分散は
\(\small{ \ s^2=\displaystyle \frac{(a-\overline{x})^2\times2n+(b-\overline{x})^2\times n}{3n}\\
=\displaystyle \frac{1}{3}\left\{\displaystyle \frac{2}{9}(a-b)^2+\displaystyle \frac{4}{9}(b-a)^2\right\}\\
=\displaystyle \frac{2}{9}(b-a)^2 \ }\)
\(\small{ \ \therefore s=\displaystyle \frac{\sqrt{2}}{3}(b-a) \ }\)
よって\(\small{ \ a \ }\)点を取った学生の偏差値は
\(\small{ \ \mathrm{T_a}=\displaystyle \frac{a-\overline{x}}{s}\times10 +50\\
=\displaystyle \frac{3}{\sqrt{2}(b-a)}\left(a-\displaystyle \frac{2a+b}{3}\right)\times10+50\\
=50-5\sqrt{2} \ }\)
\(\small{ \ b \ }\)点を取った学生の偏差値は
\(\small{ \ \mathrm{T_b}=\displaystyle \frac{b-\overline{x}}{s}\times10 +50\\
=\displaystyle \frac{3}{\sqrt{2}(b-a)}\left(b-\displaystyle \frac{2a+b}{3}\right)\times10+50\\
=50+10\sqrt{2} \ }\)
Point
①偏差値の仕組みをしっかりと理解しよう
②偏差値を求めるには元のデータの標準偏差と平均値が必要

