こんにちは、リンス(@Lins016)です。
今回は箱ひげ図とヒストグラムについて学習していこう。
箱ひげ図やヒストグラムからデータのポイントを読み取ろう
センター試験や定期試験では、ヒストグラムと箱ひげ図の関係や、その図で表されたデータがどのようなデータか読み取る力が必要になる。
だから、箱ひげ図やヒストグラムではどこに注目すればいいのか、いくつかのグラフを見ながら学習していこう。
ヒストグラム
階級の幅を底辺、度数を高さとする長方形を隙間なく順に書いたグラフ

箱ひげ図
最大値・最小値をひげ(線)で、四分位数を箱(長方形)で表した図
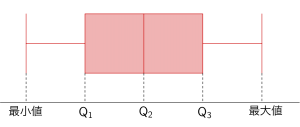
箱ひげ図の書き方
箱ひげ図を書くために、まずはデータを大きさの順に並び替えよう。
データを大きさの順に並び替えたら、最大値・最小値・第\(\small{ \ 1 \ }\)四分位数・第\(\small{ \ 2 \ }\)四分位数・第\(\small{ \ 3 \ }\)四分位数を調べよう。
各四分位数の求め方は「データの散らばりと四分位数・四分位範囲」を確認しておこう。
各数値を調べたら、まず第\(\small{ \ 1 \ }\)四分位数と第\(\small{ \ 3 \ }\)四分位数を両端にする長方形を書こう。
その長方形を第\(\small{ \ 2 \ }\)四分位数で分割しよう。これで箱の部分が完成だ。
あとはこの箱から最大値と最小値のひげを書こう。
この五つの数値を書いたら箱ひげ図の完成だ。
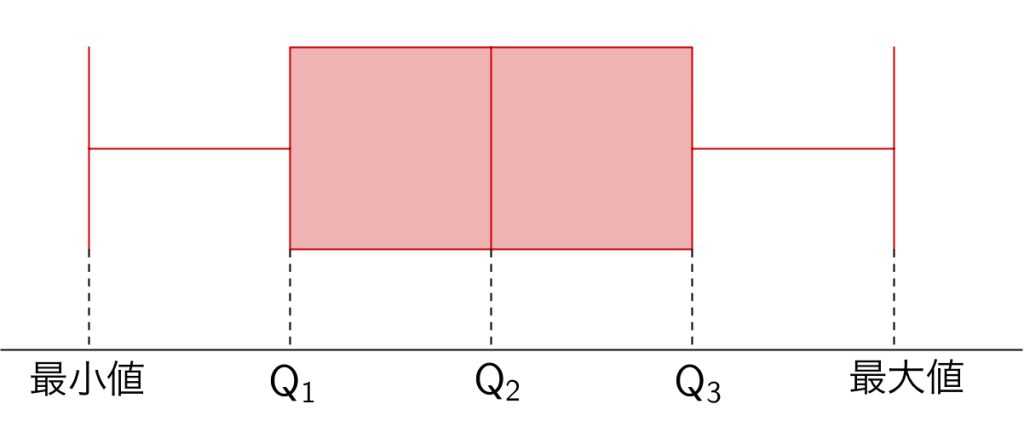
箱ひげ図とヒストグラム
今回は\(\small{ \ 5 \ }\)組の\(\small{ \ 68 \ }\)人の点数のデータを利用して、度数分布表とヒストグラムと箱ひげ図の関係を確認していこう。
まずグラフから読み取れることとして「箱ひげ図では各数値(最小値・第\(\small{ \ 1 \ }\)四分位数・第\(\small{ \ 2 \ }\)四分位数・第\(\small{ \ 3 \ }\)四分位数・最大値)の間に全体の約\(\small{ \ 25 \ }\)%のデータが入っている」ってことを常に頭に入れておこう。
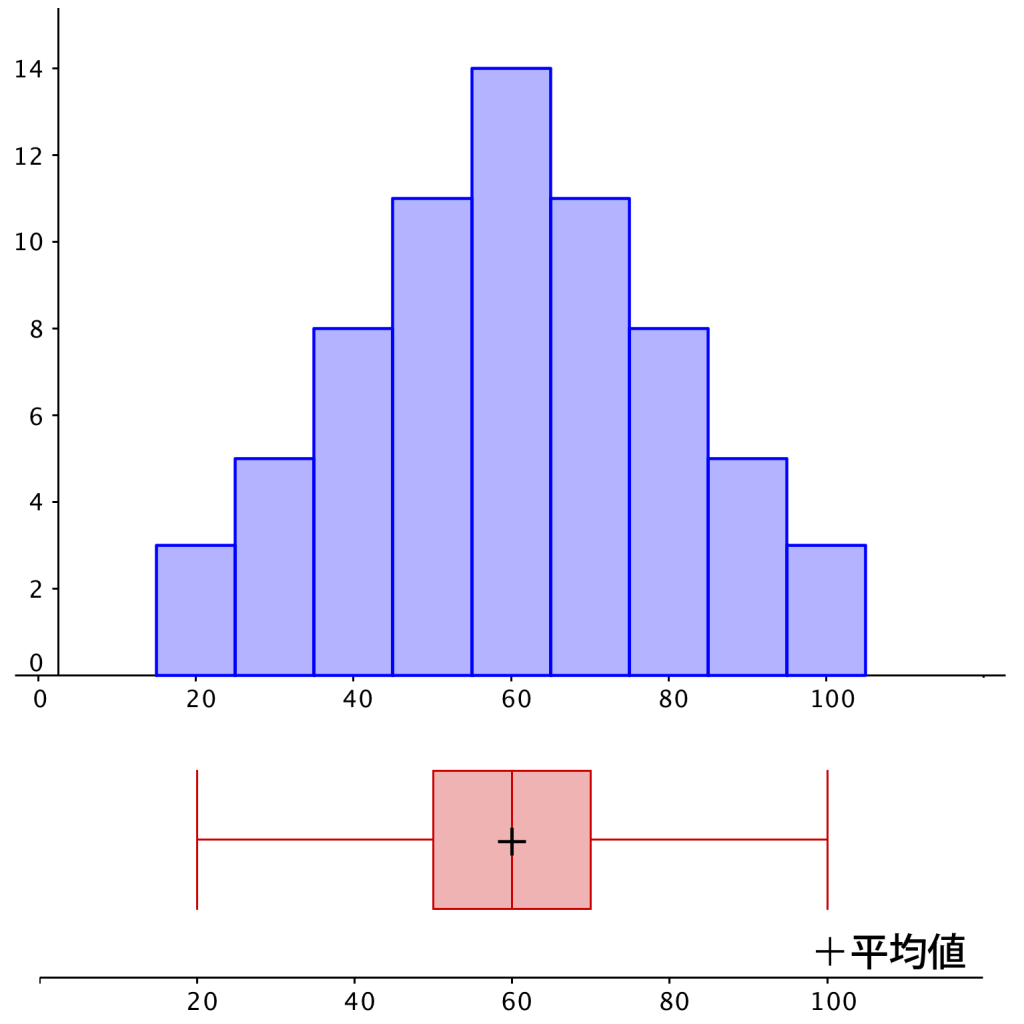
データ①
\hline
点数 & 20&30&40&50&60&70&80&90&100 \\
\hline
人数& 3&5&8&11&14&11&8&5&3 \\
\hline
\end{array} \ }\)
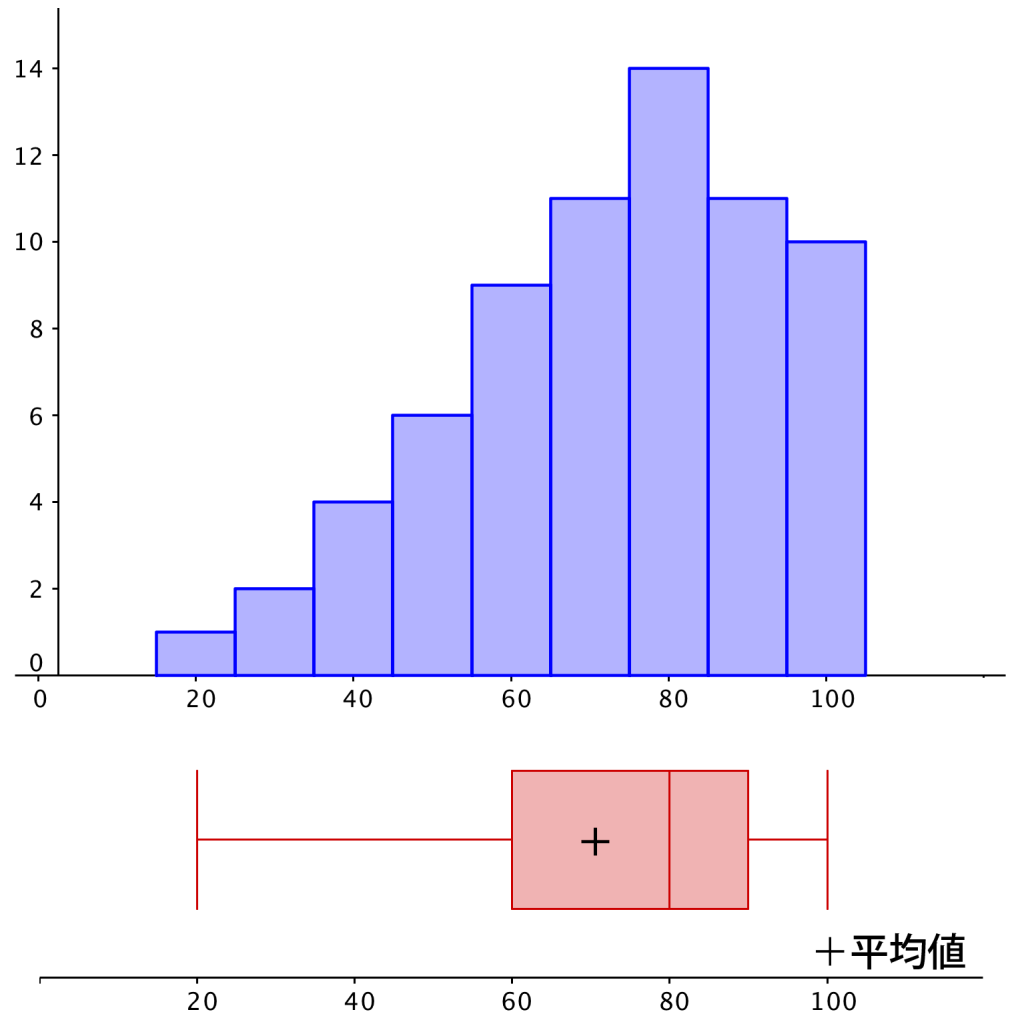
データ②
\hline
点数 & 20&30&40&50&60&70&80&90&100 \\
\hline
人数& 1&2&4&6&9&11&14&11&10 \\
\hline
\end{array} \ }\)
データ③
\hline
点数 & 20&30&40&50&60&70&80&90&100 \\
\hline
人数& 10&11&14&11&9&6&4&2&1 \\
\hline
\end{array} \ }\)
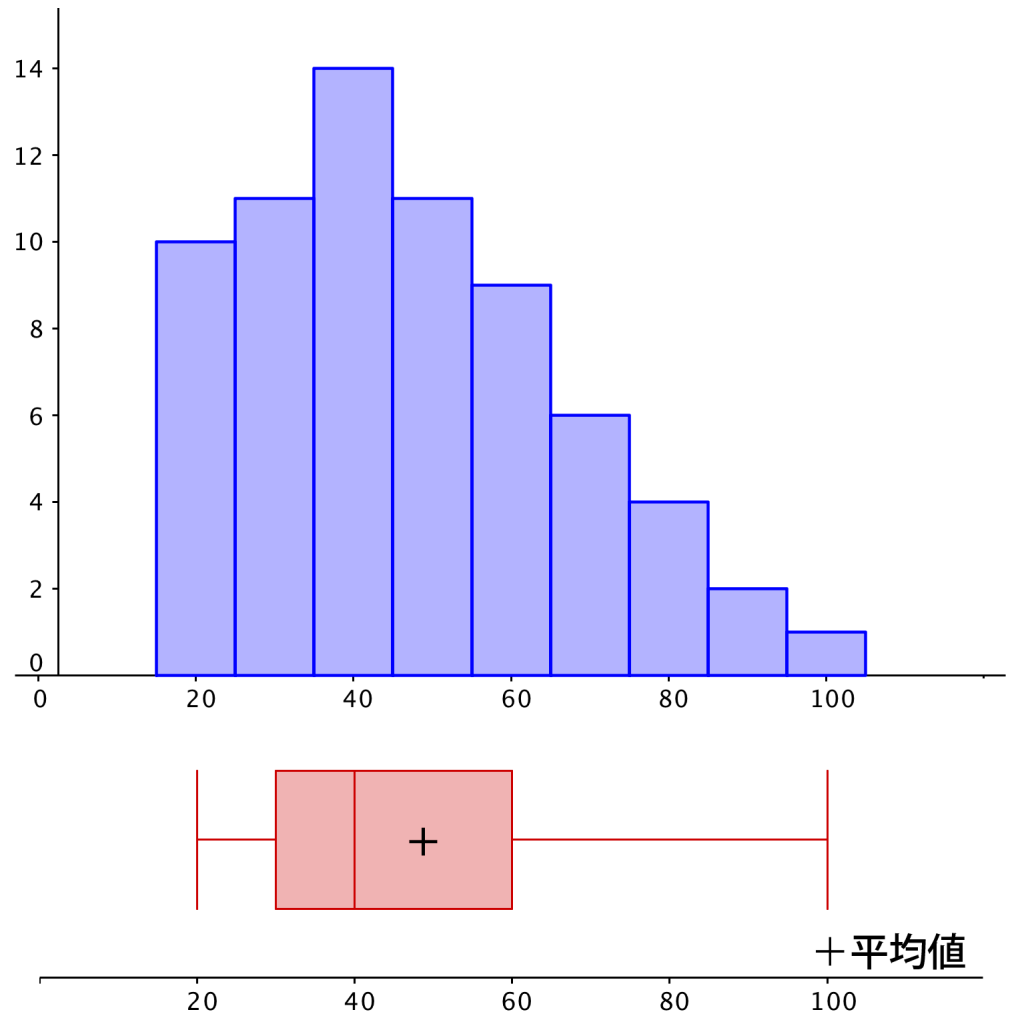
データ④
\hline
点数 & 20&30&40&50&60&70&80&90&100 \\
\hline
人数& 13&8&6&5&4&5&6&8&13 \\
\hline
\end{array} \ }\)
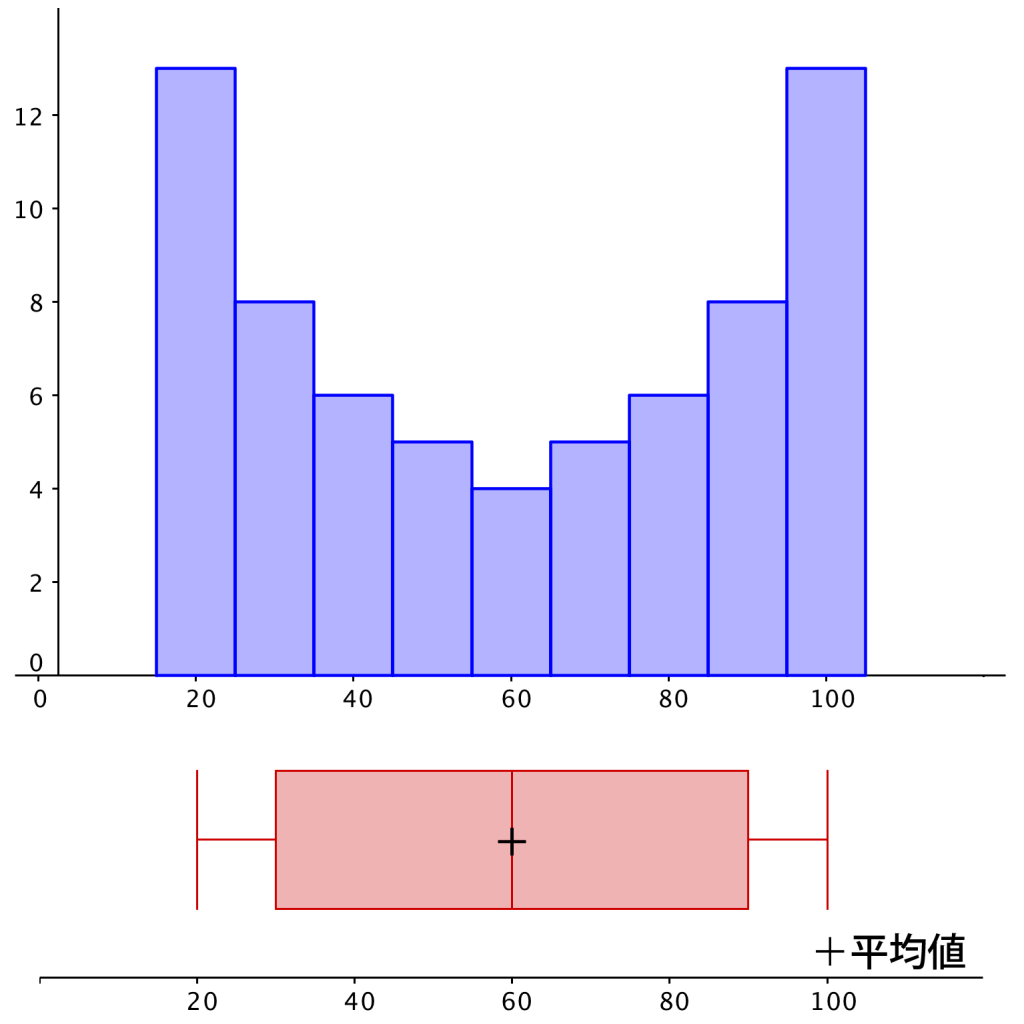
データ⑤
\hline
点数 & 20&30&40&50&60&70&80&90&100 \\
\hline
人数& 7&7&8&8&8&8&8&7&7 \\
\hline
\end{array} \ }\)
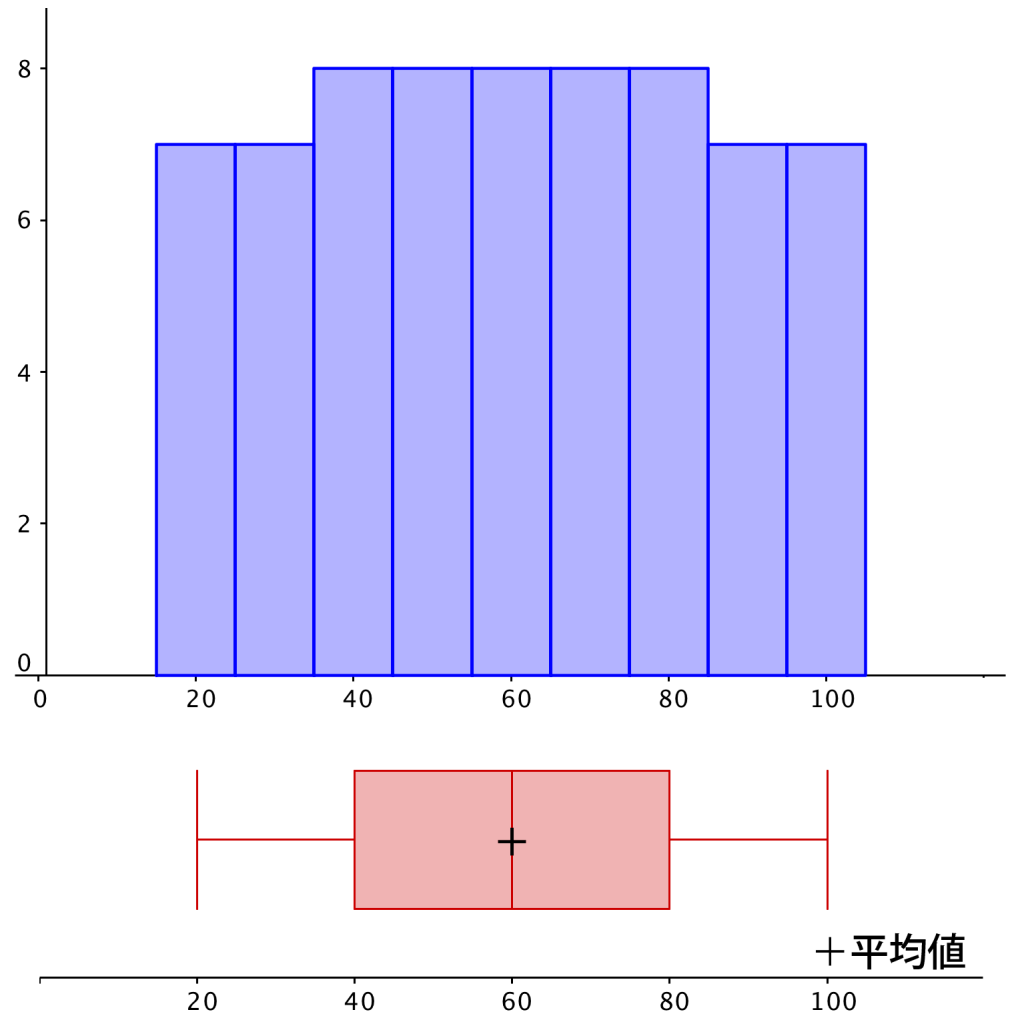
今回は分かりやすく平均値も箱ひげ図に書き込んでるけど、試験では書き込みがないと思うから、どのあたりが平均値になるのかってことも考えてみよう。
最小値・第\(\small{ \ 1 \ }\)四分位数・第\(\small{ \ 2 \ }\)四分位数・第\(\small{ \ 3 \ }\)四分位数・最大値の間にはおよそ\(\small{ \ 25 \ }\)%の人が入っていることを考えると、各数値の間隔が広い場合にはデータが散らばっているし、各数値の間隔が狭い場合は、データが集中しているってことになるよね。
データが集中しているってことはヒストグラムの長方形の高さが高いってことになるからね。
このデータには度数分布表も掲載してあるから平均値を求めるのは難しくないよね。
もちろん度数分布表がなくてもヒストグラムから度数分布表を書くことはできるからヒストグラムがあれば平均値を求めることはできるよね。
でも、度数分布表とヒストグラムがない場合、箱ひげ図だけで平均値を求めるのは無理だから、思い込みで勝手に平均値を決めつけたりしないようにしよう。
おおよその平均値はこの辺りにあるかなってぐらいは言えてもそれも正しくはないからね。
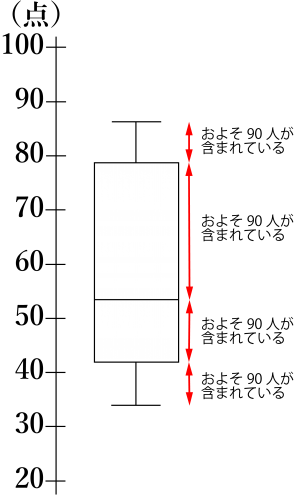
図はある高校\(\small{ \ 3 \ }\)年生\(\small{ \ 360 \ }\)人に行った定期試験の点数の箱ひげ図である。この箱ひげ図から読み取れることとして正しいものを次の中から選べ。
①\(\small{ \ 30 \ }\)点台の生徒は\(\small{ \ 90 \ }\)人である。
②\(\small{ \ 50 \ }\)点以上の生徒は\(\small{ \ 270 \ }\)人以上いる。
③\(\small{ \ 60 \ }\)点未満の生徒は半数以上いる。
④\(\small{ \ 75 \ }\)点以上の生徒は\(\small{ \ 90 \ }\)人以上いる。

③④
①について、\(\small{ \ 30 \ }\)点台の生徒は\(\small{ \ 90 \ }\)人より少ない。
②について、\(\small{ \ 40 \ }\)点以上の生徒は\(\small{ \ 270 \ }\)人以上いる。
図はある高校\(\small{ \ 3 \ }\)年生\(\small{ \ 400 \ }\)人に行った定期試験の英語と数学の点数の箱ひげ図である。この箱ひげ図から読み取れることとして正しいものを次の中から選べ。
①\(\small{ \ 60 \ }\)点以上の生徒は、英語では\(\small{ \ 200 \ }\)人以上、数学では\(\small{ \ 300 \ }\)人以上いる。
②\(\small{ \ 80 \ }\)点以上の生徒は英語では\(\small{ \ 100 \ }\)人以下、数学では\(\small{ \ 100 \ }\)人以上いる。
③\(\small{ \ 20 \ }\)点台の生徒は英語のテストにはいるが、数学のテストにはいない。
④\(\small{ \ 30 \ }\)点台の生徒は英語にはいないが、数学にはいる。
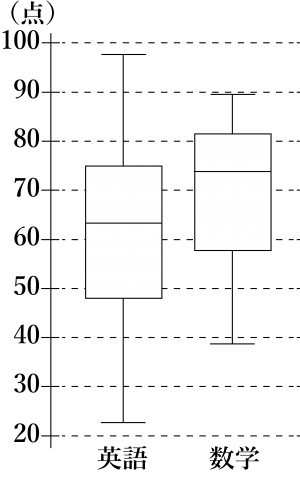
②③
①について、\(\small{ \ 60 \ }\)点以上の生徒は、英語では\(\small{ \ 200 \ }\)人以上いるが、数学では\(\small{ \ 300 \ }\)人以上いない。
④について、数学の一番低い点数は\(\small{ \ 30 \ }\)点台であるから数学には\(\small{ \ 30 \ }\)点台の生徒はいる。英語について、一番低い点数は\(\small{ \ 20 \ }\)点台である。箱ひげ図だけでは最小値の\(\small{ \ 20 \ }\)点台から第\(\small{ \ 1 \ }\)四分位数の\(\small{ \ 40 \ }\)点台後半の間に約\(\small{ \ 100 \ }\)人の生徒がいることがわかるが、英語に\(\small{ \ 30 \ }\)点台の生徒いるかいないかは正確に判断できない。つまり\(\small{ \ 30 \ }\)点台の生徒がいないとは言えないため不適。


Point
①箱ひげ図の書き方をマスターしよう
②箱ひげ図とヒストグラムの関係(市分位数同士の間隔とヒストグラムの長方形の高さの関係)を読み取れるようになろう

