ド・モアブルの定理

こんにちは、リンス(@Lins016)です。
今回はド・モアブルの定理について学習していこう。

ド・モアブルの定理の証明

ド・モアブルの定理

\(\small{ \ z=\cos\theta+i\sin\theta \ }\)のとき
\(\small{ \ z^n=\cos n\theta+i\sin n\theta \ }\)
ただし\(\small{ \ n \ }\)は整数

nが自然数のとき

\(\small{ \ \left(\cos\theta+i\sin\theta\right)^n=\cos n\theta+i\sin n\theta \ }\)
まずは\(\small{ \ n \ }\)が正の整数の場合について、数学的帰納法を用いて証明してみよう。

(i)\(\small{ \ n=1 \ }\)のとき
両辺ともに\(\small{ \ \cos\theta+i\sin\theta \ }\)より成り立つ
(ii)\(\small{ \ n=k \ }\)のとき
\(\small{ \ \left(\cos\theta+i\sin\theta\right)^k=\cos k\theta+i\sin k\theta \ }\)が成り立つと仮定する
両辺に\(\small{ \ \cos\theta+i\sin\theta \ }\)をかけると

\(\small{\begin{eqnarray} \ \left(\cos\theta+i\sin\theta\right)^{k+1}&=&\left(\cos k\theta+i\sin k\theta\right)\left(\cos\theta+i\sin\theta\right)\\[3pt] &=&\cos k\theta\cos\theta-\sin k\theta\sin\theta+i\left(\sin k\theta\cos\theta+\cos k\theta\sin\theta\right)\\[3pt] &=& \cos(k+1)\theta+i\sin (k+1)\theta \ \end{eqnarray}}\)

よって\(\small{ \ n=k+1 \ }\)のときも成り立つ
(i)(ii)よりすべての自然数\(\small{ \ n \ }\)で\(\small{ \ \left(\cos\theta+i\sin\theta\right)^n=\cos n\theta+i\sin n\theta \ }\)が成り立つ

nが負の整数のとき

次に\(\small{ \ n \ }\)が負の整数の場合について、証明してみよう。

\(\small{ \ n=-m \ (m\geqq1) \ }\)とすると

\(\small{\begin{eqnarray} \ \left(\cos\theta+i\sin\theta\right)^n&=&\left(\cos\theta+i\sin\theta\right)^{-m}\\[3pt] &=&\displaystyle\frac{1}{\left(\cos\theta+i\sin\theta\right)^m}\\[3pt] &=&\displaystyle\frac{1}{\cos m\theta+i\sin m\theta}\\[3pt] &=&\displaystyle\frac{1}{\cos\left(-n\theta\right)+i\sin\left(-n\theta\right)}\\[3pt] &=&\displaystyle\frac{1}{\cos n\theta-i\sin n\theta}\\[3pt] &=&\displaystyle\frac{\cos n\theta+i\sin n\theta}{\left(\cos n\theta-i\sin n\theta\right)\left(\cos n\theta+i\sin n\theta\right)}\\[3pt] &=&\displaystyle\frac{\cos n\theta+i\sin n\theta}{\cos^2 n\theta+\sin^2 n\theta}\\[3pt] &=&\cos n\theta+i\sin n\theta \ \end{eqnarray}}\)

よって\(\small{ \ n \ }\)が負の整数のときも成り立つ

n=0のとき

最後に\(\small{ \ n=0 \ }\)の場合について、証明してみよう
(左辺)\(\small{ \ =\left(\cos\theta+i\sin\theta\right)^0=1 \ }\)
(右辺)\(\small{ \ =\cos0+i\sin0=1 \ }\)
よって成り立つ

これでド・モアブルの定理がすべての整数のときに成り立つことが分かったよね。

図形的な意味

\(\small{ \ z=\cos\theta+i\sin\theta \ }\)のとき\(\small{ \ z \ }\)は単位円周上にあるよね。

ド・モアブルの定理から\(\small{ \ z^2, \ z^3, \ z^4,\cdots \ }\)はすべて単位円周上にあるし、各点は\(\small{ \ \theta \ }\)ずつ回転させた下図のようになるんだ。

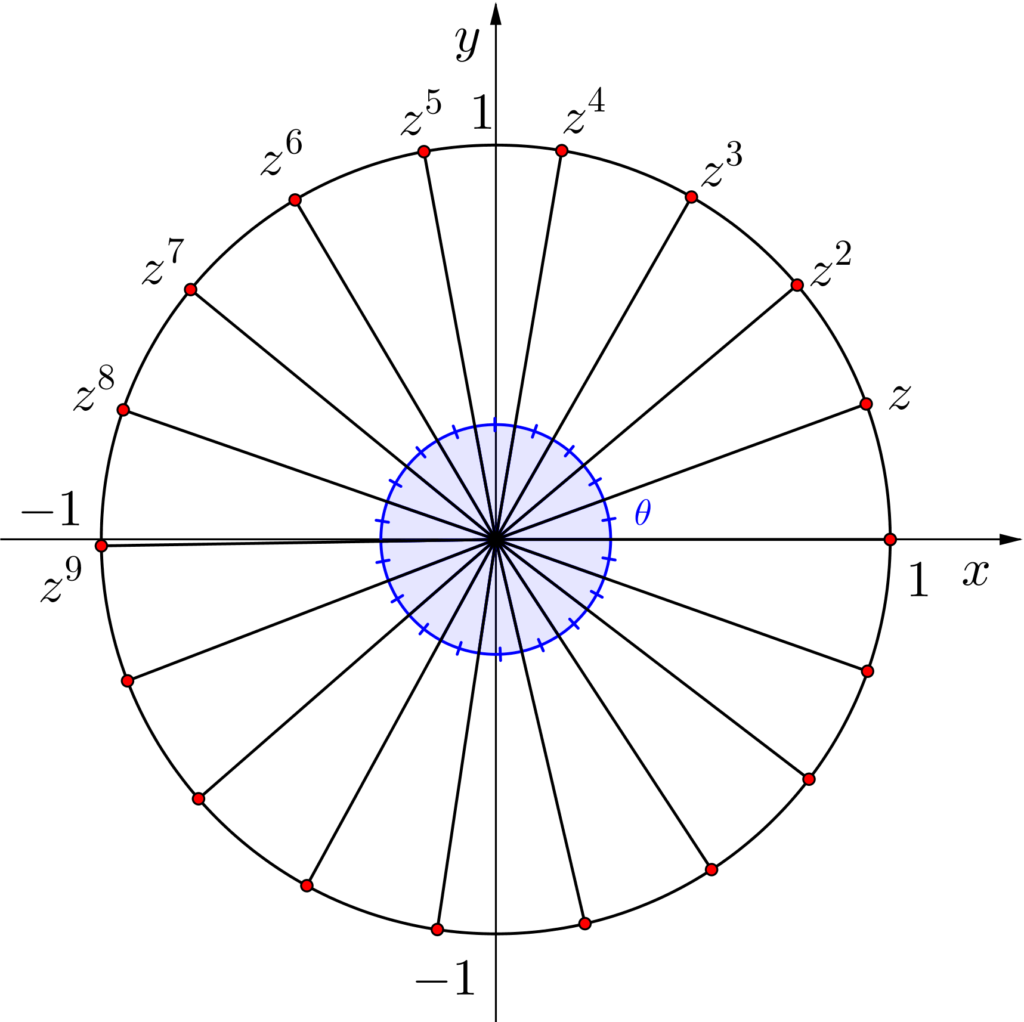
だから、単位円周上にある複素数\(\small{ z }\)は何乗しても単位円周上にあるし、\(\small{ \ z^n \ }\)が単位円周上にあれば、\(\small{ \ z \ }\)も単位円周上にあるってことが言えるんだ。

このあたりは\(\small{ \ z^n=1 \ }\)の方程式にもつながってるよね。