こんにちは、リンス(@Lins016)です。
今回は円と放物線の位置関係と交点の数について学習していこう。
円と放物線の位置関係
円と放物線の位置関係から交点を求めるのは、円と放物線で囲まれた面積を求めるときによく利用する。
だから出題されるとしたら積分の範囲が多いけど、位置関係だけなら図形と方程式になるから、今回はよく出題される円の中心の\(\small{ \ x \ }\)座標と放物線の軸が一致する場合の円と放物線の位置関係と交点の個数について学習していこう。
①円の中心と放物線の軸が同じ場合は連立方程式は\(\small{ \ y \ }\)で解く
②\(\small{ \ y \ }\)の二次方程式が解を持つ条件を考える
③\(\small{ \ 1 \ }\)個の解を持つときが円と放物線が接するときだとはいえない
円と放物線の共有点(交点)の求め方
例えば\(\small{ \ x^2+y^2=1 \ }\)と\(\small{ \ y=x^2 \ }\)の交点を求めるとき、この円と放物線の式を連立したらいいよね。
\(\small{ \begin{eqnarray}
\left\{
\begin{array}{l}
x^2+y^2=1\\
y=x^2
\end{array}
\right.
\end{eqnarray} \ }\)
連立方程式を見ると\(\small{ \ y \ }\)を消去して\(\small{ \ x \ }\)の式を立てたくなるけど、今回は\(\small{ \ y \ }\)の式を立てよう。やることはそこまで変わらないけど、計算量や解の個数が変わってくるのがわかるよね。
ちなみに\(\small{ \ y \ }\)を消去すると\(\small{ \ x^2+x^4=1 \ }\)になって\(\small{ \ x \ }\)の四次方程式、一応\(\small{ \ t=x^2 \ }\)とおくと\(\small{ \ t^2+t-1=0 \ }\)になって二次方程式にはなるけど面倒だよね。
はじめから\(\small{ \ x \ }\)を消去すると\(\small{ \ y^2+y-1=0 \ }\)になる。断然こっちが楽だよね。
円と放物線の共有点の個数と交わるパターン
円と放物線の位置関係は全部で\(\small{ \ 8 \ }\)パターンある。
(1)交点\(\small{ \ 0 \ }\)個

(2)交点\(\small{ \ 2 \ }\)個
\(\small{ \ y \ }\)座標の値:\(\small{ \ 1 \ }\)つ
\(\small{ \ x \ }\)座標の値:\(\small{ \ 2 \ }\)つ
円と放物線は接している

(3)交点\(\small{ \ 4 \ }\)個
\(\small{ \ y \ }\)座標の値:\(\small{ \ 2 \ }\)つ
\(\small{ \ x \ }\)座標の値:\(\small{ \ 4 \ }\)つ

(4)交点\(\small{ \ 3 \ }\)個
\(\small{ \ y \ }\)座標の値:\(\small{ \ 2 \ }\)つ
\(\small{ \ x \ }\)座標の値:\(\small{ \ 3 \ }\)つ
円と放物線は接している
(5)交点\(\small{ \ 2 \ }\)個
\(\small{ \ y \ }\)座標の値:\(\small{ \ 1 \ }\)つ
\(\small{ \ x \ }\)座標の値:\(\small{ \ 2 \ }\)つ

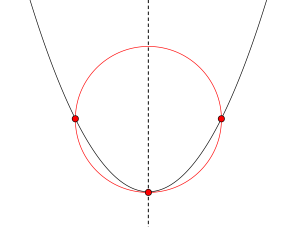
(6)交点\(\small{ \ 1 \ }\)個
\(\small{ \ y \ }\)座標の値:\(\small{ \ 1 \ }\)つ
\(\small{ \ x \ }\)座標の値:\(\small{ \ 1 \ }\)つ
円と放物線は接している

(7)交点\(\small{ \ 0 \ }\)個

(8)交点\(\small{ \ 1 \ }\)個
\(\small{ \ y \ }\)座標の値:\(\small{ \ 1 \ }\)つ
\(\small{ \ x \ }\)座標の値:\(\small{ \ 1 \ }\)つ
円と放物線は接している

円の中心を放物線の軸に沿って移動させたとき、放物線の頂点と円の一番下の点が重なる場合、半径や放物線の傾きによって(4)か(8)の形になる。どちらの形になるかは調べてみないとわからないから注意しよう。
また、円と放物線が接するときって、円と放物線の方程式を連立させて\(\small{ \ x \ }\)を消去して\(\small{ \ y \ }\)の二次方程式を考えるんだけど、この\(\small{ \ 8 \ }\)個の形を確認してもわかるけど、解が\(\small{ \ 1 \ }\)つだからといって接するとは限らないよね。そこのところに注意して次の例題を解いてみよう。
放物線\(\small{ \ y=x^2 \ }\)と円\(\small{ \ x^2+(y-a)^2=1 \ }\)との共有点の個数を求めよ。
\(\small{\begin{eqnarray}
\left\{
\begin{array}{l}
y=x^2\cdots①\\
x^2+(y-a)^2=1\cdots②
\end{array}
\right.
\end{eqnarray} \ }\)
\(\small{ ①}\)を\(\small{ ② }\)に代入して
\(\small{ \ y+(y-a)^2=1 \ }\)
\(\small{ \ y^2-(2a-1)y+a^2-1=0 \cdots③ }\)
円と放物線が接するときについて考えると

図の状態になるのは\(\small{ ③}\)が正の重解を持つときより
\(\small{ \ D=(2a-1)^2-4(a^2-1)=0 \ }\)かつ\(\small{ \ 2a-1\gt0 \ }\)
\(\small{ \ \therefore a=\displaystyle \frac{5}{4} \ }\)
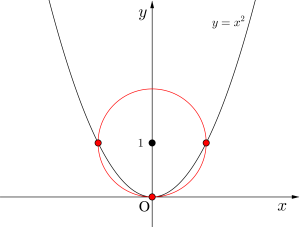
また次に円の一番下が原点で接する場合について考える
これは原点を通るから円の中心と半径が等しいので\(\small{ \ a=1 \ }\)
\(\small{ ③}\)に代入すると
\(\small{ \ y^2-y=0 \ }\)
\(\small{ \ y(y-1)=0 \ \ \therefore y=0, \ 1 \ }\)
よって\(\small{ \ a=1 \ }\)のとき3点で交わる
また円の一番上の点が原点で接する場合について考える
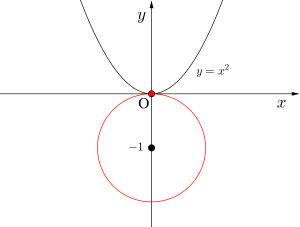
これは原点を通るから円の中心と半径が等しいので、円の中心の\(\small{ \ y \ }\)座標が負に注意して\(\small{ \ a=-1 \ }\) となる。
これより
\(\small{ \ a \gt \displaystyle \frac{5}{4} \ }\)のとき交点\(\small{ \ 0 \ }\)個
\(\small{ \ a = \displaystyle \frac{5}{4} \ }\)のとき交点\(\small{ \ 2 \ }\)個
\(\small{ \ 1 \lt a \lt \displaystyle \frac{5}{4} \ }\)のとき交点\(\small{ \ 4 \ }\)個
\(\small{ \ a =1 \ }\)のとき交点\(\small{ \ 3 \ }\)個
\(\small{ \ -1\lt a \lt 1 \ }\)のとき交点\(\small{ \ 2 \ }\)個
\(\small{ \ a =-1 \ }\)のとき交点\(\small{ \ 1 \ }\)個
\(\small{ \ a \lt 1 \ }\)のとき交点\(\small{ \ 0 \ }\)個

\(\small{ \ y^2+3y=0 \ }\)
\(\small{ \ y(y+3)=0 \ }\)
\(\small{ \ \therefore y=0, \ -3 \ }\)ってなるけど、放物線は\(\small{ \ y=x^2 \ }\)だから交点の\(\small{ \ y\geqq0 \ }\)じゃないとダメだよね。
つまり\(\small{\begin{eqnarray}
\left\{
\begin{array}{l}
y=x^2\\
x^2+(y-a)^2=1
\end{array}
\right.
\end{eqnarray} \ }\)と\(\small{ \ y^2-(2a-1)y+a^2-1=0 \ }\)は同値じゃないってことがわかるよね。
確かに連立方程式では\(\small{ \ y\geqq0 \ }\)だけど、二次方程式では \(\small{ \ y \ }\)はなんでもいいもんね。図も考えながら定義域に注意して問題を解くようにしよう。
Point 円と放物線の位置関係と交点の数
①円と放物線の式を連立する
②連立するときは\(\small{ \ x=y \ }\)の式にして\(\small{ \ x \ }\)を消去が基本
③定義域に注意して判別式や方程式を解く
\(\small{ \ a \ }\)を正の定数とし、放物線\(\small{ \ y=ax^2 \ }\)と直線\(\small{ \ y=1 \ }\)で囲まれる領域を\(\small{ \ D \ }\)とする。
\(\small{ \ y \ }\)軸上の点を中心とする領域\(\small{ \ D \ }\)に含まれる円の半径の最大値を求めよ。
円の半径を\(\small{ \ r \ }\)とすると\(\small{ \ 2r \leqq1 \ }\)より\(\small{ \ r \leqq\displaystyle \frac{1}{2} \ }\)
(i)\(\small{ \ r=\displaystyle \frac{1}{2} \ }\)のとき
このとき\(\small{ \ y=ax^2 \ }\)と\(\small{ \ x^2+\left(y-\displaystyle \frac{1}{2}\right)^2=\displaystyle \frac{1}{4} \ }\)の共有点が原点のみでなければならないので
\(\small{ \ \displaystyle \frac{y}{a}+y^2-y=0 \ }\)
\(\small{ \ y\left(y-1+\displaystyle \frac{1}{a}\right)=0 \ }\)
\(\small{ \ 1-\displaystyle \frac{1}{a}\leqq 0 \ }\) \(\small{ \ \therefore a\leqq 1 \ }\)
(ii)\(\small{ \ a \ge 1 \ }\)のとき
円の中心を\(\small{ \ (0, \ b) \ }\)とすると
\(\small{ \ x^2+(y-b)^2=r^2 \ }\)
この円と\(\small{ \ y=ax^2 \ }\)が接するので
\(\small{ \ \displaystyle \frac{y}{a}+y^2-2by+b^2-r^2=0 \ }\)
\(\small{ \ y \ }\)の値が1つになるのでこの方程式の判別式を\(\small{ \ D_1 \ }\)とすると
\(\small{ \ D_1=\left(\displaystyle \frac{1}{a}-2b\right)^2-4(b^2-r^2)=0 \ }\)
\(\small{ \ \displaystyle \frac{1}{a^2}-\displaystyle \frac{4b}{a}+4r^2=0\cdots① \ }\)
また円が領域\(\small{ \ D \ }\)の内部にあるので
\(\small{ \ b+r\leqq 1\cdots② \ }\)
\(\small{①}\)を\(\small{ ② }\)に代入すると
\(\small{ \ \displaystyle \frac{1}{4a}+ar^2+r\leqq1 \ }\)
\(\small{ \ \left(r+\displaystyle \frac{1}{2a}\right)^2\leqq\displaystyle \frac{1}{a} \ }\)
\(\small{ \ r\leqq -\displaystyle \frac{1}{2a}+\displaystyle \frac{1}{\sqrt{a}} \ }\)
よって\(\small{ \ r \ }\)の最大値は
\(\small{ \ r=\displaystyle \frac{2\sqrt{a}-1}{2a} \ }\)


