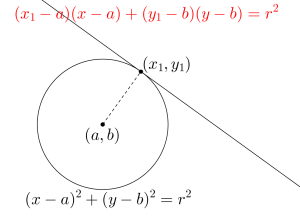こんにちは、リンス(@Lins016)です。
今回は円の接線の方程式の公式の証明について学習していこう。
スポンサーリンク
円の接線の公式の求め方
円の接線の公式
\(\small{ \ (x-a)^2+(y-b)^2=r^2 \ }\)上の\(\small{ \ (x_1, \ y_1) \ }\)における接線の方程式\(\small{(x_1-a)(x-a)+(y_1-b)(y-b)=r^2}\)
特に円の中心が原点のとき
\(\small{x_1x+y_1y=r^2}\)
円の接線の公式の証明
接点と中心を結ぶ直線の傾きは\(\small{\displaystyle \frac{y_1-b}{x_1-a}}\)より
求める接線は、この傾きに垂直で接点\(\small{(x_1,y_1)}\)を通る直線だから、
\(\small{y-y_1=-\displaystyle \frac{x_1-a}{y_1-b}(x-x_1)}\)
ただし\(\small{ \ y_1\neq b \ }\)とする。
\(\small{(y-y_1)(y_1-b)=-(x_1-a)(x-x_1)}\)
\(\small{(y-b+b-y_1)(y_1-b)=-(x_1-a)(x-a+a-x_1)}\)
\(\small{(y-b)(y_1-b)-(y_1-b)^2=-(x_1-a)(x-a)+(x_1-a)^2}\)
\(\small{(x_1-a)(x-a)+(y-b)(y_1-b)=(x_1-a)^2+(y_1-b)^2}\)
\(\small{(y-b+b-y_1)(y_1-b)=-(x_1-a)(x-a+a-x_1)}\)
\(\small{(y-b)(y_1-b)-(y_1-b)^2=-(x_1-a)(x-a)+(x_1-a)^2}\)
\(\small{(x_1-a)(x-a)+(y-b)(y_1-b)=(x_1-a)^2+(y_1-b)^2}\)
\(\small{ \ (x_1, \ y_1) \ }\)は円周上の点だから
\(\small{ \ (x_1-a)^2+(y_1-b)^2=r^2 \ }\)
\(\small{\therefore (x_1-a)(x-a)+(y-b)(y_1-b)=r^2}\)
これは\(\small{ \ y_1=b \ }\)のときも満たす。
