こんにちは、リンス(@Lins016)です。
今回は順列と英字の並び方について学習していこう。
順列と英字の並び方
英字の並び替えには、問題文が条件を指定して並び替える問題と辞書式配列(辞書式順序)に並び替える問題がある。
今回はこの二つの問題について考えていくよ。ただ今回考えるのは、readingのような全部異なる文字の並び方。internetのように同じ文字(e,t)が二つ以上入っている問題は、また別で考えるからね。
全て異なる英字の並び方
①問題文が条件を指定する問題
②辞書式配列(辞書式順序)
異なる文字の並び方
問題文が条件を指定する問題について考えてみよう。
全部異なる文字の並び替えの場合、前回学習した「順列と人の並び方」と同じ考え方ができるんだ。
人が男子、女子ってグループに分けられるように、英字も母音(a,i,u,e,o)と子音(母音以外)に分けられるしね。
だからreading(母音\(\small{ \ 3 \ }\)文字、子音\(\small{ \ 4 \ }\)文字)の並べ替えの問題の場合、男子\(\small{ \ 3 \ }\)人、女子\(\small{ \ 4 \ }\)人を並び替える問題と同じような内容の問題になるんだ。
下の二つの例題で確認してみよう。
readingの文字をすべて用いる順列で、次の並び方は何通りあるか。
(1)両端が子音である。
(2)両端のうち少なくとも一つは子音である。
(3)母音は隣り合わない。
(4)rとaの間に二文字入る。
男子3人女子4人が一列に並ぶとき、次の並び方は何通りあるか。
(1)両端が女子である。
(2)両端のうち少なくとも一人は女子である。
(3)男子は隣り合わない。
(4)特定の二人の間に二人入る。
答えは問題1・問題2ともに共通
(1)\(\small{ \ _4\mathrm{P}_2\times 5!\\
=1440 \ }\)
(2)\(\small{ \ 7!-_3\mathrm{P}_2\times 5!\\
=5!(7\times6-3\times2)\\
=4320 \ }\)
(3)\(\small{ \ 4!\times _5\mathrm{P}_3\\
=1440 \ }\)
(4)\(\small{ \ _5\mathrm{P}_2\times 2!\times 4!\\
=960 \ }\)

順列と辞書式配列(辞書式順序)
次は英単語を辞書式配列について並び替える問題について確認していこう。
この辞書式配列の問題は二つの問いがある。
それは
「○○○○○は前から数えて何番目の文字列か?」
「前から数えて○○番目の文字列は何か?」の二つ何だ。
まずは辞書式配列の考え方を学習していこう。
例としてbeautyについて考えてみよう。
まずbeautyを辞書式配列に並べたときの一番最初の文字は、アルファベット順(ABC順)に並べ替えてabetuy。
これはアルファベット順に並び替えただけだから大丈夫だよね。
この次の単語は一番後ろを並び替えてabetyu。
後ろの二つを入れ替えたものになる。
次々に考えていくと
abeuty
abeuyt
abeytu
abeyut
\(\small{ \ \ \ \ \vdots \ }\)
って続いてく。
とにかく、この並びの法則で押さえておきたいのは、先頭の文字を定めた場合のこと。
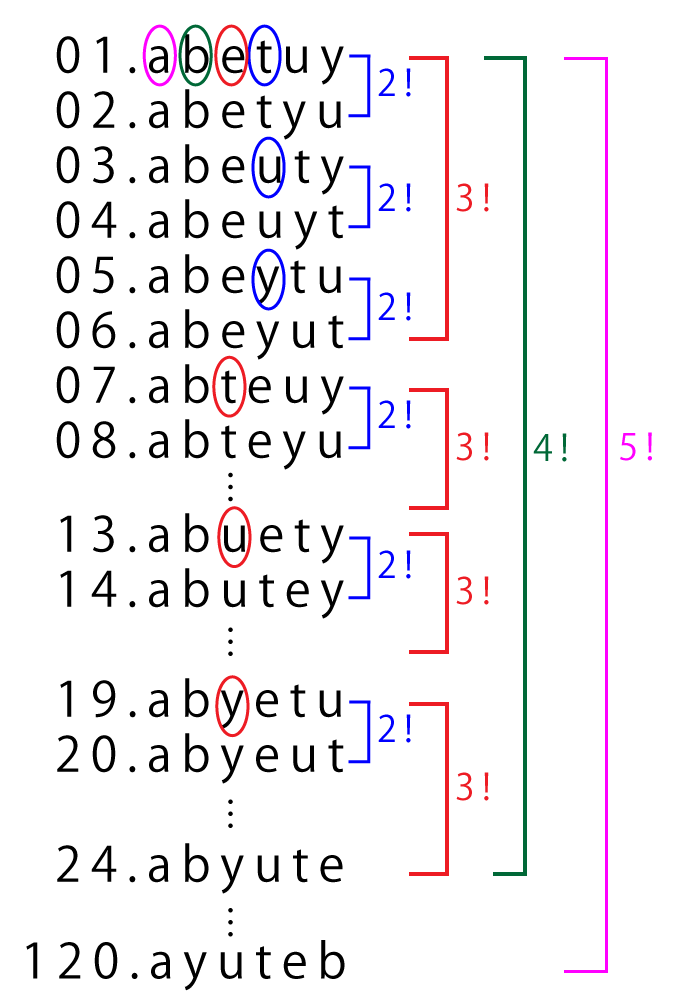

辞書式配列のポイントは先頭の文字列が〇〇の時、何通りあるか絞り込んでいくってところなんだ。
まずは先頭の文字を定めよう。先頭の文字列を定めたら、先頭がその文字列の並び方は、先頭の文字列を除いた残りの文字数の階乗通りあるからね。
次に先頭の文字列を定めたら、残った文字列もアルファベット順に並べていかないといけないからね。
このことを頭に入れて例題を考えてみよう。
beautyの\(\small{ \ 6 \ }\)文字を全て使ってできる順列をabetuyを\(\small{ \ 1 \ }\)番目として辞書式に並べるとき次の問いに答えよ。
(1)\(\small{ \ 160 \ }\)番目の文字列を答えよ。
(2)ybetauは何番目の文字列か求めよ。
(1)辞書式配列の\(\small{ \ 1 \ }\)番目はabetuy
aから始まる順列は全部で\(\small{ \ 5!=120 \ }\)通り
次のbから始まる順列も全部で\(\small{ \ 5!=120 \ }\)通り
よって\(\small{ \ 160 \ }\)番目の文字列はbから始まる順列である
baから始まる文字列は\(\small{ \ 4!=24 \ }\)通り
beから始まる文字列も\(\small{ \ 4!=24 \ }\)通り
よって\(\small{ \ 160 \ }\)番目の文字列はbeから始まる順列である
beaから始まる文字列は\(\small{ \ 3!=6 \ }\)通り
betから始まる文字列も\(\small{ \ 3!=6 \ }\)通り
beuから始まる文字列も\(\small{ \ 3!=6 \ }\)通り
よって\(\small{ \ 160 \ }\)番目の文字列はbeuから始まる順列である
beuから始まる文字列の一番最初の文字列はbeuaty
これは\(\small{ \ 120+24+6+6+1=157 \ }\)番目
\(\small{ \ 158 \ }\)番目はbeuayt
\(\small{ \ 159 \ }\)番目はbeutay
よって\(\small{ \ 160 \ }\)番目はbeutya
(2)aで始まる文字列は\(\small{ \ 5!=120 \ }\)通り
bで始まる文字列は\(\small{ \ 5!=120 \ }\)通り
eで始まる文字列は\(\small{ \ 5!=120 \ }\)通り
tで始まる文字列は\(\small{ \ 5!=120 \ }\)通り
uで始まる文字列は\(\small{ \ 5!=120 \ }\)通り
yaで始まる文字列は\(\small{ \ 4!=24 \ }\)通り
ybaで始まる文字列は\(\small{ \ 3!=6 \ }\)通り
ybeaで始まる文字列は\(\small{ \ 2!=2 \ }\)通り
この次がybetauになる
よってybetauは
\(\small{ \ 120\times5+24+6+2+1=633 \ }\)番目である。

Point 順列と英単語の並び替え
①条件指定の問題は異なる文字だけなら人の並び方と同じ
②条件部分から式を考える
③辞書式配列は先頭の文字を決定して絞り込む
\(\small{ \ \def\cenBox#1{\bbox[3px, border:2px solid]{\ \bf{ #1 }\ }}\def\cenbox#1{\bbox[4px, border:1px solid gray]{\ #1\ }} \ }\)A,B,C,D,E,Fの\(\small{ \ 6 \ }\)文字を\(\small{ \ 1 \ }\)列に並べることを考える。
(1)EとFの間に(あるいはFとEの聞にといってもよいが、)ちょうど\(\small{ \ 3 \ }\)文字が並ぶ並ベ方は\(\small{ \ \cenbox{ア} \ }\)通りある。またEとFの間にちようど\(\small{ \ 2 \ }\)文字が並ぶ並べ方は\(\small{ \ \cenbox{イ} \ }\)通りあり、ちょうど\(\small{ \ 1 \ }\)文字が並ぶ並ベ方は\(\small{ \ \cenbox{ウ} \ }\)通りある。
(2)EとFが隣り合わない並ベ方は\(\small{ \ \cenbox{エ} \ }\)通りある。
(3)EとFの間に並ぶ文字の中に、Aが入る並ベ方は\(\small{ \ \cenbox{オ} \ }\)通りあり、EとFの間に並ぶ文字の中に、AとBがともに入る並ベ方は\(\small{ \ \cenbox{カ} \ }\)通りある。また,EとFの間に並ぶ文字の中に、Cが入らない並ベ方は\(\small{ \ \cenbox{キ} \ }\)通りある。
(1)ア:\(\small{ \ _{4}\mathrm{P}_{3}\times2!\times2!=96 \ }\)
イ:\(\small{ \ _{4}\mathrm{P}_{2}\times2!\times3!=144 \ }\)
ウ:\(\small{ \ _{4}\mathrm{P}_{1}\times2! \times4!=192 \ }\)
(2)エ:\(\small{ \ 4! \times_{5}\mathrm{P}_{2}=480 \ }\)
別解(余事象)
\(\small{ \ 6!-5! \times2!=480 \ }\)
(3) オ:\(\small{ \ _{6}\mathrm{P}_{3} \times2!=240 \ }\)
カ:\(\small{ \ _{6}\mathrm{P}_{2}\times2! \times2!=120 \ }\)
キ:EとFの間に並ぶ文字の中にCが入る並べ方は、EとFの間に並ぶ文字の中にAが入る並ベ方と同じだから余事象を利用して
\(\small{ \ 6!-240=480 \ }\)