こんにちは、リンス(@Lins016)です。
今回は同じものを含む順列と組合せについて学習していきましょう。
同じものを含む順列と組合せ
同じものを含む順列と組合せは考え方は同じだから、まとめて考えていくことにしよう。同じものを含む順列は、定期試験や大学入試でもよく出題されるからきちんと理解しておこう。
\(\small{ \ a \ }\)が\(\small{ \ p \ }\)個、\(\small{ \ b \ }\)が\(\small{ \ q \ }\)個、\(\small{ \ c\ }\)が\(\small{ \ r \ }\)個の合計\(\small{ \ n \ }\)個(\(\small{ \ p+q+r=n \ }\))の並べ方
\(\small{ \ {}_n\mathrm{C}_p \times {}_{n-p}\mathrm{C}_q \times {}_{n-p-q}\mathrm{C}_r=\displaystyle\frac{n!}{p!q!r!} \ }\)
同じものを含む順列の基本
まずは\(\small{ \ a, \ a, \ a, \ b, \ b \ }\)を並べ方について考えてみよう。
\(\small{ \ a, \ b\ }\)は区別がつかないけど、区別がつくとして考えてみよう。
つまり\(\small{ \ a_1, \ a_2, \ a_3, \ b_1, \ b_2 \ }\)の並べ方を考えるってことね。
\(\small{ \ a, \ a, \ a, \ b, \ b \ }\)という\(\small{ \ 1 \ }\)通りの並べ方は区別がつくと
①\(\small{ \ a_1, \ a_2, \ a_3, \ b_1, \ b_2 \ }\)
②\(\small{ \ a_1, \ a_3, \ a_2, \ b_1, \ b_2 \ }\)
③\(\small{ \ a_2, \ a_1, \ a_3, \ b_1, \ b_2 \ }\)
④\(\small{ \ a_2, \ a_3, \ a_1, \ b_1, \ b_2 \ }\)
⑤\(\small{ \ a_3, \ a_1, \ a_2, \ b_1, \ b_2 \ }\)
⑥\(\small{ \ a_3, \ a_2, \ a_1, \ b_1, \ b_2 \ }\)
⑦\(\small{ \ a_1, \ a_2, \ a_3, \ b_2, \ b_1 \ }\)
⑧\(\small{ \ a_1, \ a_3, \ a_2, \ b_2, \ b_1 \ }\)
⑨\(\small{ \ a_2, \ a_1, \ a_3, \ b_2, \ b_1 \ }\)
⑩\(\small{ \ a_2, \ a_3, \ a_1, \ b_2, \ b_1 \ }\)
⑪\(\small{ \ a_3, \ a_1, \ a_2, \ b_2, \ b_1 \ }\)
⑫\(\small{ \ a_3, \ a_2, \ a_1, \ b_2, \ b_1 \ }\)
つまり\(\small{ \ a_1, \ a_2, \ a_3 \ }\)の並べ方\(\small{ \ 3! \ }\)通りと\(\small{ \ b_1, \ b_2 \ }\)の並べ方\(\small{ \ 2! \ }\)通りをかけた\(\small{ \ 12 \ }\)通りあることになるよね。
区別が付かないと\(\small{ \ a, \ a, \ a, \ b, \ b \ }\)の\(\small{ \ 1 \ }\)通り、区別がつくと\(\small{ \ 3!\times2!=12 \ }\)通りになるから、全てを並べる場合、全部区別が付くとして考えて、それを後から\(\small{ \ 3!\times2!=12 \ }\)で割ってあげればいいんだ。
だから\(\small{ \ a, \ a, \ a, \ b, \ b \ }\)を並べ方は、\(\small{ \ \displaystyle\frac{5!}{3!2!}=10 \ }\)通りになるんだ。
同じものを含む順列と組合せ
次に\(\small{ \ a, \ a, \ a, \ b, \ b \ }\)の並べ方を組合せで考えてみよう。
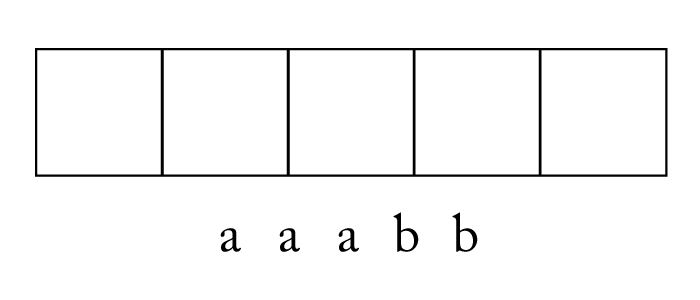
図の\(\small{ \ 5 \ }\)つの場所のうち\(\small{ \ a \ }\)を入れるところを\(\small{ \ 3 \ }\)つ選ぶと、残ったところには自動的に\(\small{ \ b \ }\)が入るよね。
だから、この並べ方は\(\small{ \ a \ }\)を入れるところを\(\small{ \ 5 \ }\)つの場所から\(\small{ \ 3 \ }\)つ選べばいいから\(\small{ \ {}_5\mathrm{C}_3 \ }\)通りになるよね。
\(\small{ \ b \ }\)を入れるところを\(\small{ \ 5 \ }\)つの場所から\(\small{ \ 2 \ }\)つ選んでもいいから\(\small{ \ {}_5\mathrm{C}_2 \ }\)通りとも言えるよね。
\(\small{ \ {}_n\mathrm{C}_r={}_n\mathrm{C}_{n-r} \ }\)だから\(\small{ \ {}_5\mathrm{C}_3={}_5\mathrm{C}_2 \ }\)になるからね。
結局\(\small{ \ a, \ b \ }\)それぞれの順序は考えずに\(\small{ \ a, \ b \ }\)を置く場所だけ考えればいいから、組合せで考えることが出来るんだ。
ちなみに\(\small{ \ {}_n\mathrm{C}_r=\displaystyle\frac{n!}{r!(n-r)!} \ }\)だから\(\small{ \ {}_5\mathrm{C}_3={}_5\mathrm{C}_2=\displaystyle\frac{5!}{3!2!} \ }\)ってなって、さっきの\(\small{ \ a, \ b \ }\)を区別して考える場合と同じ計算式になってるよね。
この組合せの階乗の計算はよく使うからきちんと覚えておこう。
『同じものを含む順列の問題』は『組合せの問題』とも言えるからね。
複数の同じものを含む順列
次に\(\small{ \ a, \ a, \ a, \ b, \ b, \ c, \ c, \ c, \ d \ }\)のべ方について考えてみよう。
さっきと同じで\(\small{ \ a_1, \ a_2, \ a_3, \ b_1, \ b_2, \ c_1, \ c_2, \ c_3, \ d \ }\)のように区別がつくと考えると
全部の並べ方は\(\small{ \ 9! \ }\)通り
\(\small{ \ a_1, \ a_2, \ a_3 \ }\)の並べ方は\(\small{ \ 3! \ }\)通り
\(\small{ \ b_1, \ b_2 \ }\)の並べ方は\(\small{ \ 2! \ }\)通り
\(\small{ \ c_1, \ c_2, \ c_3 \ }\)の並べ方は\(\small{ \ 3! \ }\)通り
\(\small{ \ d \ }\)の並べ方は\(\small{ \ 1! \ }\)通り
だから\(\small{ \ a, \ a, \ a, \ b, \ b, \ c, \ c, \ c, \ d \ }\)の並べ方は
\(\small{ \ \displaystyle\frac{9!}{3!2!3!1!}=5040 \ }\)通りになるんだ。
これを一般化すると、\(\small{ \ a \ }\)が\(\small{ \ p \ }\)個、\(\small{ \ b \ }\)が\(\small{ \ q \ }\)個、\(\small{ \ c\ }\)が\(\small{ \ r \ }\)個(\(\small{ \ p+q+r=n \ }\))の並べ方は
\(\small{ \ \displaystyle\frac{n!}{p!q!r!} \ }\)通りになるからね。
複数の同じものを含む順列と組合せ
さらに\(\small{ \ a, \ a, \ a, \ b, \ b, \ c, \ c, \ c, \ d \ }\)の並べ方を組合せで考えてみよう。
まずは、図の\(\small{ \ 9 \ }\)つの場所のうち\(\small{ \ a \ }\)を入れるところを\(\small{ \ 3 \ }\)つ選ぶ。この選び方は\(\small{ \ {}_9\mathrm{C}_3 \ }\)通りだよね。
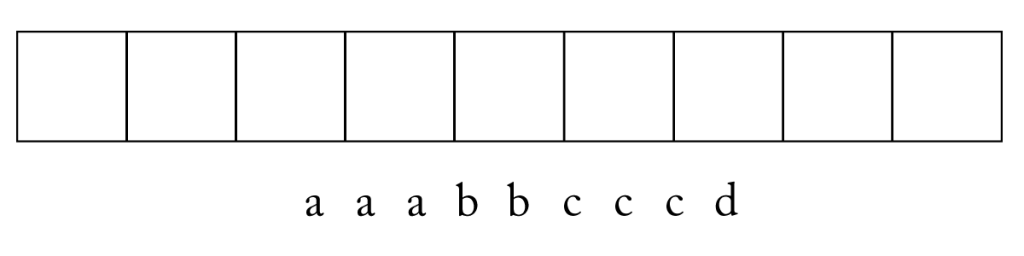
次に残った\(\small{ \ 6 \ }\)つの場所のうち\(\small{ \ b \ }\)を入れるところを\(\small{ \ 2 \ }\)つ選ぶ。この選び方は\(\small{ \ {}_6\mathrm{C}_2 \ }\)通りだよね。
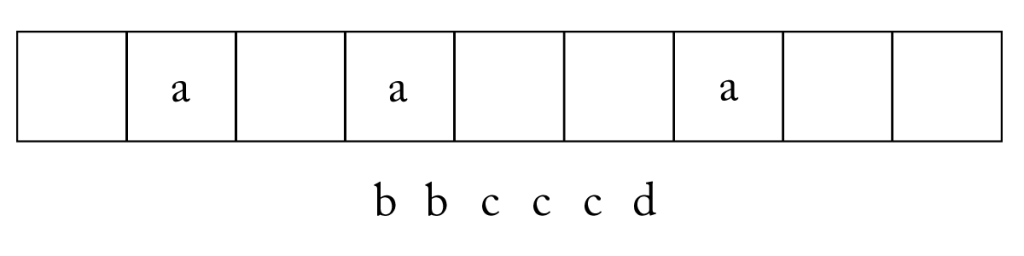
最後に残った\(\small{ \ 4 \ }\)つの場所のうち\(\small{ \ c \ }\)を入れるところを\(\small{ \ 3 \ }\)つ選ぶ。
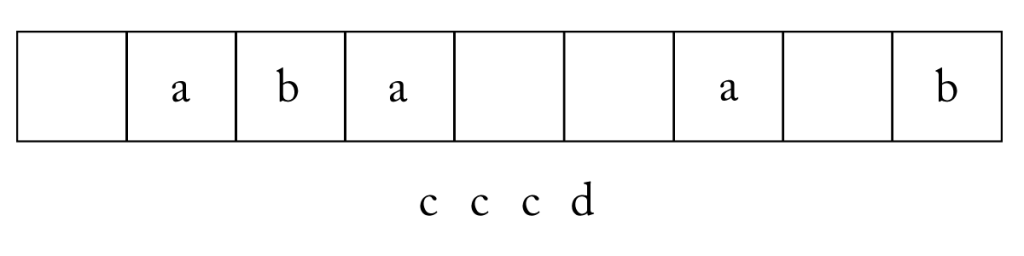
すると残った\(\small{ \ 1 \ }\)つの場所に\(\small{ \ d \ }\)が自動的に入るからね。この選び方は\(\small{ \ {}_4\mathrm{C}_3 \ }\)通りだよね。
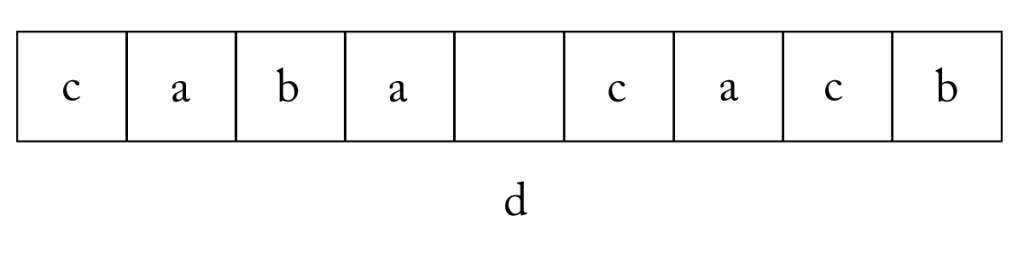
だから求める並べ方は
\(\small{ \ {}_9\mathrm{C}_3\times {}_6\mathrm{C}_2\times {}_4\mathrm{C}_3=5040 \ }\)通りになる。
つまり順番を無視して、それぞれの文字の入る部分だけを考えていくんだ。
これを一般化してみると
\(\small{ \ a \ }\)が\(\small{ \ p \ }\)個、\(\small{ \ b \ }\)が\(\small{ \ q \ }\)個、\(\small{ \ c\ }\)が\(\small{ \ r \ }\)個(\(\small{ \ p+q+r=n \ }\))の並べ方は
\(\small{ \ {}_n\mathrm{C}_p \times {}_{n-p}\mathrm{C}_q \times {}_{n-p-q}\mathrm{C}_r \ }\)
これを階乗を利用して書くと
\(\small{ \ {}_n\mathrm{C}_p \times {}_{n-p}\mathrm{C}_q \times {}_{n-p-q}\mathrm{C}_r \ }\)
\(\small{ \ =\displaystyle\frac{n!}{p!q!r!} \ (\because \ n=p+q+r) \ }\)
この場合も『同じものを含む順列の問題』は『組合せの問題』って言えるよね。
\(\small{ \ 6 \ }\)個の文字\(\small{ \ \mathrm{K, \ A, \ G, \ A, \ K, \ U} \ }\)を並べるとき、次の問いに答えよ。
(1)\(\small{ \ 6 \ }\)個の文字全てを一列に並べるとき、並べ方は何通りあるか。
(2)\(\small{ \ 6 \ }\)個の文字から\(\small{ \ 4 \ }\)個の文字を選んで一列に並べるとき、並べ方は何通りあるか。
(1)\(\small{ \ \mathrm{K} \ }\)と\(\small{ \ \mathrm{A} \ }\)は\(\small{ \ 2 \ }\)個ずつあるので\(\small{ \ 6 \ }\)個の文字を一列に並べるのは
\(\small{ \ \displaystyle\frac{6!}{2!2!}=180 \ }\)通り
(2)\(\small{ \ 6 \ }\)個の中から\(\small{ \ 4 \ }\)個選ぶとき同じ文字を選ぶか選ばないかに着目すると
①文字が\(\small{ \ 2 \ }\)種類
②文字が\(\small{ \ 3 \ }\)種類
③文字が\(\small{ \ 4 \ }\)種類
の\(\small{ \ 3 \ }\)つの場合がある。
①のとき\(\small{ \ \mathrm{K, \ K, \ A, \ A} \ }\)になるので、この並び方は
\(\small{ \ \displaystyle\frac{4!}{2!2!}=6 \ }\)通り
②のとき\(\small{ \ \mathrm{K} \ }\)\(\small{ \ 2 \ }\)個と\(\small{ \ \mathrm{A, \ G, \ U} \ }\)のうちから\(\small{ \ 2 \ }\)個
または\(\small{ \ \mathrm{A} \ }\)\(\small{ \ 2 \ }\)個と\(\small{ \ \mathrm{K, \ G, \ U} \ }\)のうちから\(\small{ \ 2 \ }\)個
よってこの\(\small{ \ 4 \ }\)個の文字を一列に並べるのは
\(\small{ \ \displaystyle\frac{4!}{2!}\times {}_3\mathrm{C}_2 \times2=72 \ }\)通り
③のとき\(\small{ \ \mathrm{K, \ A, \ G, \ U} \ }\)の\(\small{ \ 4 \ }\)個の文字を一列に並べるのは
\(\small{ \ 4!=24 \ }\)通り
よって求める答えは
\(\small{ \ 6+72+24=102 \ }\)通り

Point 同じものを含む順列と組合せ
①全てを区別して計算し、同じものの数の階乗で割る
②順番を無視した組合せとして考える。

