こんにちは、リンス(@Lins016)です。
今回は円順列とじゅず順列について学習していきましょう。
じゅず順列とは
じゅず順列とは、ものを円形に並べる順列で、裏返しによって並び方が一致するものを同じとみなす順列のこと。
裏返しにする分、円順列より数が少ないことを頭に入れておこう。
・\(\small{ \ n \ }\)個の異なるものを並べる場合
円順列
\(\small{ \ \displaystyle\frac{n!}{n}=(n-1)! \ }\)
じゅず順列
\(\small{ \ \displaystyle\frac{(n-1)!}{2} \ }\)
・同じものを含む円順列・じゅず順列の場合
円順列
同じものが一つもないものを固定し、残りを同じものを含む順列として考える
じゅず順列
円順列のうち裏返して同じになる円順列とそうでない円順列にわけ、そうでない方を\(\small{ \ 2 \ }\)で割る、
じゅず順列の基本
まずはじゅず順列の基本を考えてみよう。
異なる\(\small{ \ 8 \ }\)個のものを円形に並べてみよう。
その並べ方の数は円順列だから\(\small{ \ \displaystyle\frac{8!}{8}=7!=5040 \ }\)通りになるよね。
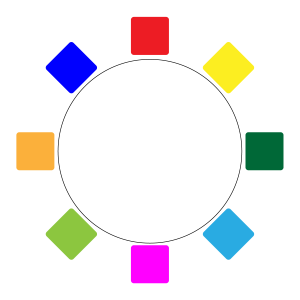
この\(\small{ \ 5040 \ }\)通りのうち、下図の\(\small{ \ 2 \ }\)つの並べ方は異なるよね。

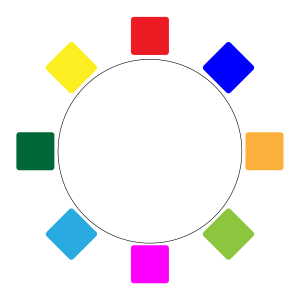
でもこれがじゅず順列だとしたら、裏返しにすると同じ並べ方になるから、円順列だと\(\small{ \ 2 \ }\)通りだけど、じゅず順列だと\(\small{ \ 1 \ }\)通りになるんだ。
つまり異なるものを円形に並べるとき、円順列には\(\small{ \ 1 \ }\)つの並べ方を裏返しにしたものが必ず一つ存在するから、じゅず順列の並べ方は円順列の並べ方の数を\(\small{ \ 2 \ }\)で割ってあげればいいんだ。
だから一般化すると、\(\small{ \ n \ }\)個の異なるものを並べる場合、円順列だと\(\small{ \ \displaystyle\frac{n!}{n}=(n-1)! \ }\)通り、じゅず順列だと\(\small{ \ \displaystyle\frac{(n-1)!}{2} \ }\)通りになる。
同じものを含む円順列
同じものを含む円順列の問題について考えてみよう。
図のように赤\(\small{ \ 1 \ }\)個、青\(\small{ \ 2 \ }\)個、緑\(\small{ \ 3 \ }\)個、黄\(\small{ \ 2 \ }\)個、黒\(\small{ \ 1 \ }\)個の合計\(\small{ \ 9 \ }\)個並べる場合、単純に\(\small{ \ \displaystyle\frac{9!}{9} \ }\)通りとはできないよね。
だって同じものは区別できないからね。
まずは円順列の手順どおり\(\small{ \ 1 \ }\)つのものを固定しよう。
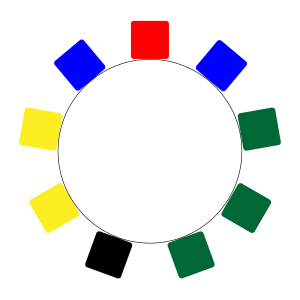
円順列を忘れている人は一度チェックしておこう。
この場合、固定するものは複数あるものじゃなく、\(\small{ \ 1 \ }\)つしかないものにしよう。だから赤か黒ってことになるからね。赤か黒ならどっちでもいいよ。
それじゃ赤を固定して考えてみよう。
赤は\(\small{ \ 1 \ }\)個だけだから円形に並べる方法は、図の下にある赤から始まる列と\(\small{ \ 1 \ }\)対\(\small{ \ 1 \ }\)の対応になるんだ。
だから、この一列に赤以外を並べることを考えたらいいからね。
つまり\(\small{ \ \displaystyle\frac{8!}{2!3!2!1!}=1680 \ }\)通りになる。
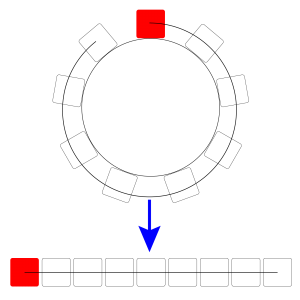
これは前回やった同じものを含む順列になるからできるよね。忘れてる人はもう一度チェックしておこう。
同じものを含むじゅず順列
じゅず順列で一番出題されるのは、この同じものを含むじゅず順列なんだ。だから確実に理解していこう。
同じものを含むじゅず順列の場合円順列で求めた答えを単純に\(\small{ \ 2 \ }\)で割ればいいってことにならないから注意しよう!
難しいからよく出題されるってことだからね。
どうして\(\small{ \ 2 \ }\)で割ればいいってことにならないかというと、次の図を見てみよう。
この図を裏返しにしても、同じものになるよね。
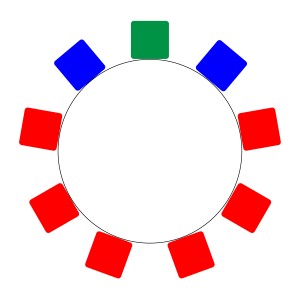
でも次の図は裏返しても同じにならないよね。
表
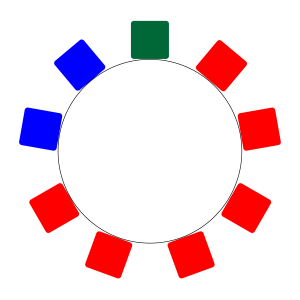
裏
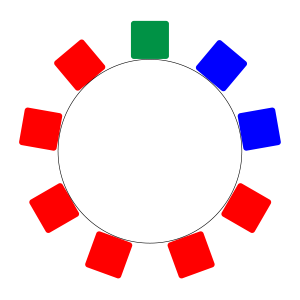
つまり今ここに挙げた\(\small{ \ 3 \ }\)つの図は、円順列では\(\small{ \ 3 \ }\)通り、じゅず順列では\(\small{ \ 2 \ }\)通りになるんだ。だから単純に\(\small{ \ 2 \ }\)で割ればいいとは言えないよね。
つまり同じものを含むと裏返しにしてもまったく同じ並べ方になる場合が存在する場合がある。
だから円順列の中から、裏返しにしてもまったく同じになる場合を除いたものを\(\small{ \ 2 \ }\)で割る必要があるんだ。
でも並べる個数や複数あるものの個数によっては裏返して同じものになるものがない場合もあるからね。
\(\small{ \ 1 \ }\)つしかないものを固定して裏返しても同じになるものが存在するか調べよう。

赤色の球が\(\small{ \ 6 \ }\)個、青色の球が\(\small{ \ 2 \ }\)個、緑色の球が\(\small{ \ 1 \ }\)個ある。これらを次のように並べるとき、その並べ方は何通りあるか。
(1)これらを一列に並べる
(2)これらを円形に並べる
(3)これらの球に糸を通し、首輪を作る
(1)同じものを含む順列になるから
\(\small{ \ \displaystyle\frac{9!}{6!2!}=252 \ }\)通り
(2)緑色を固定し、残りを一列に並べる場合の数と同じだから
\(\small{ \ \displaystyle\frac{8!}{6!2!}=28 \ }\)
(3)円順列で左右対称になるのは片側の赤\(\small{ \ 3 \ }\)個と青\(\small{ \ 1 \ }\)個の並べ方の数と等しいから
\(\small{ \ {}_4\mathrm{C}_3=4 \ }\)通り
円順列\(\small{ \ 28 \ }\)通りのうち\(\small{ \ 4 \ }\)通りが裏返しても同じだから
\(\small{ \ 4+\displaystyle\frac{28-4}{2}=16 \ }\)通り
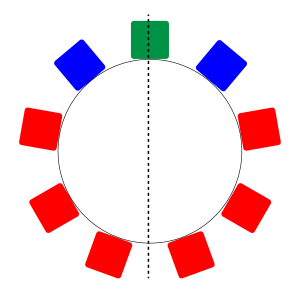

Point 円順列とじゅず順列
①異なるものを並べるじゅず順列は円順列の数を\(\small{ \ 2 \ }\)で割る
②同じものを含む円順列は一個だけしかないものを固定して一列に並べるものに置き換える
③同じものを含むじゅず順列は円順列の中から裏返しても同じになるものを求めて、それ以外を\(\small{ \ 2 \ }\)で割る

