こんにちは、リンス(@Lins016)です。
今回は完全順列について学習していこう。
完全順列とは
完全順列とは、\(\small{ \ 1,2,3・・・,n \ }\)を一列に並べた順列のうち、どの\(\small{ \ k \ }\)番目の数も\(\small{ \ k \ }\)でない順列のことなんだ。攪乱(かくらん)順列って言ったりもするかな。
この完全順列の総数を数学者のモンモールって人から名づけられてモンモール数っていうんだ。
完全順列
\(\small{ \ W(n)=n!\displaystyle \sum_{ k = 2 }^{ n }\displaystyle\frac{(-1)^k}{k!} \ }\)
完全順列の一般化
\(\small{ \ 1 \ }\)から\(\small{ \ n \ }\)までの番号のついた\(\small{ \ n \ }\)個の箱の中に、\(\small{ \ 1 \ }\)から\(\small{ \ n \ }\)までの数字が書いてある\(\small{ \ n \ }\)枚のカードを\(\small{ \ 1 \ }\)枚ずつ入れていくことを考えてみよう。
箱は\(\small{ \ 1 \ }\)から\(\small{ \ n \ }\)までが左から順に並んでいて、この一つの箱に\(\small{ \ 1 \ }\)枚のカードを入れていくとすると、箱の数字と箱の中のカードの数字が一つも同じでないものは完全順列になるよね。
この箱の数字と箱の中のカードの数字が一つも同じでない完全順列の総数を\(\small{ \ W(n) \ }\)とすると、これがモンモール数になるからね。
今回はこのモンモール数を求めてみよう。
\(\small{ \ W(n) \ }\)を考えるには、まず\(\small{ \ 1 \ }\)から\(\small{ \ n-1 \ }\)までの番号のついた\(\small{ \ n-1 \ }\)個の箱の中に\(\small{ \ 1 \ }\)から\(\small{ \ n-1 \ }\)までの数字が書いてある\(\small{ \ n-1 \ }\)枚のカードをそれぞれ\(\small{ \ 1 \ }\)枚ずつ箱に入れた状態で、ここに\(\small{ \ n \ }\)の番号のついた箱に\(\small{ \ n \ }\)と書いてあるカードが入ったものを持ってくる場合について考えてみよう。
箱と中のカードの数が1つも同じものがない
\(\small{ \ 1 \ }\)から\(\small{ \ n-1 \ }\)までの番号のついた\(\small{ \ n-1 \ }\)個の箱の中に\(\small{ \ 1 \ }\)から\(\small{ \ n-1 \ }\)までの数字の書いてある\(\small{ \ n-1 \ }\)枚のカードがそれぞれの箱に1枚ずつ入っているとき、箱の番号と中のカードの数が同じであるものが一つもないとき、この並びの総数は\(\small{ \ n-1 \ }\)個の完全順列になるから\(\small{ \ W(n-1) \ }\)通りあるよね。
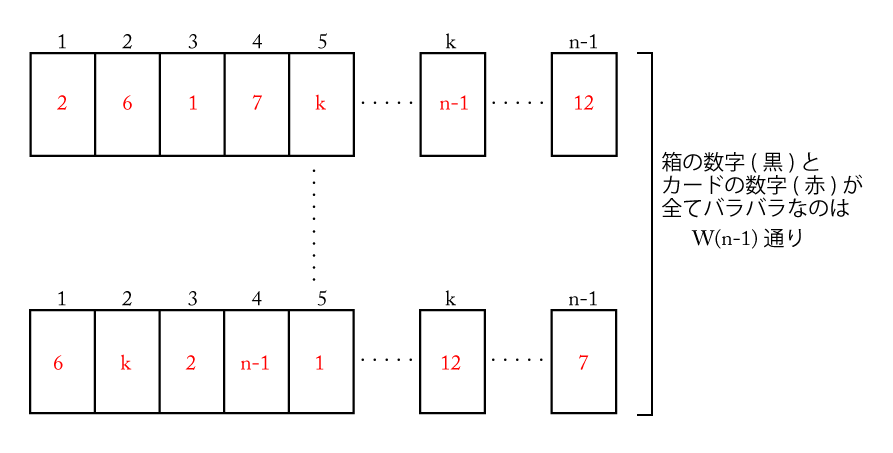
ここに\(\small{ \ n \ }\)の番号の箱に\(\small{ \ n \ }\)の数字が書いてあるカードが入ったものをもってくる。
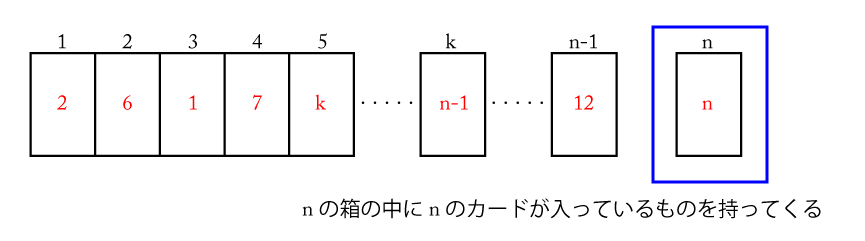
この箱の中の\(\small{ \ n \ }\)の書かれたカードと\(\small{ \ 1 \ }\)~\(\small{ \ n-1 \ }\)番までのいずれかの箱の中のカードと取り替える。このとき箱の番号と箱の中のカードの番号が同じであるものは一つもない。つまり完全順列になるよね。
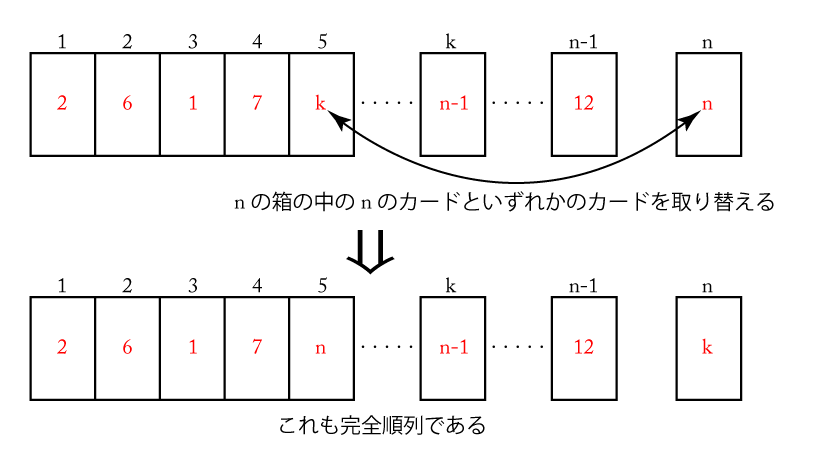
このように\(\small{ \ n \ }\)の箱の\(\small{ \ n \ }\)が書かれたカードを取り替えた完全順列の数は、\(\small{ \ n \ }\)の箱の中の\(\small{ \ n \ }\)が書かれたカードと\(\small{ \ 1 \ }\)~\(\small{ \ n-1 \ }\)までの箱の中のいずれかのカードを取り替える\(\small{ \ n-1 \ }\)通りの取り替え方があるから、全部で\(\small{ \ (n-1)\times W(n-1) \ }\)通りある。
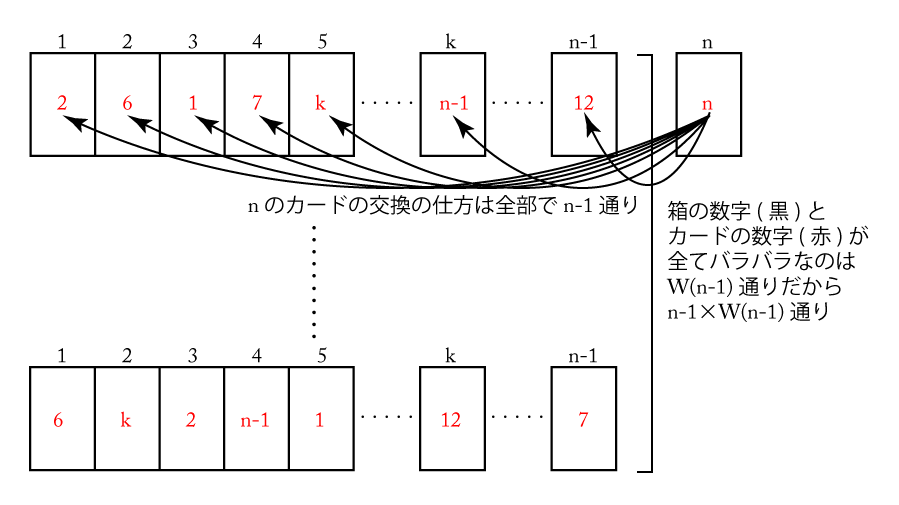
箱と中のカードの数が1つだけ同じものがある
次に\(\small{ \ 1 \ }\)から\(\small{ \ n-1 \ }\)までの\(\small{ \ n-1 \ }\)個の箱の中に\(\small{ \ 1 \ }\)つだけ、箱の番号と同じ番号のカードが入っている場合について考えてみよう。\(\small{ \ 1 \ }\)つだけ同じということは、この同じものを除いた\(\small{ \ n-2 \ }\)個の並びの総数は\(\small{ \ n-2 \ }\)個の完全順列になるから\(\small{ \ W(n-2) \ }\)通りあるよね。
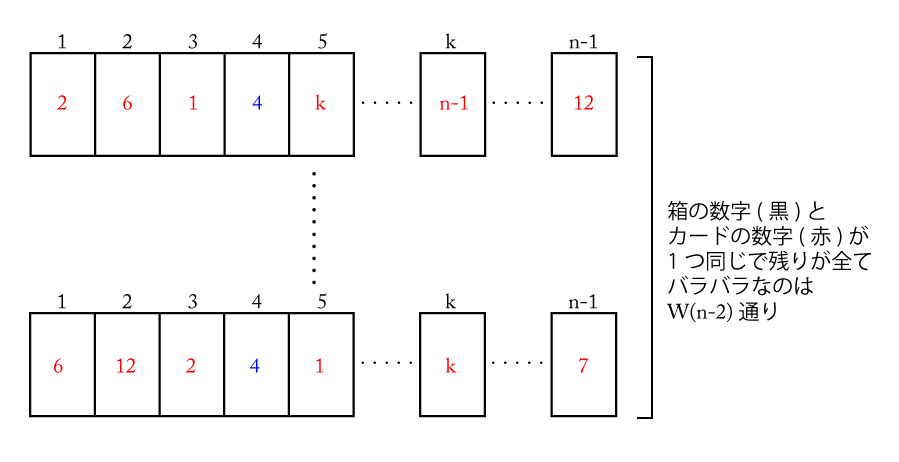
ここにさっきと同じように\(\small{ \ n \ }\)の箱に\(\small{ \ n \ }\)が書かれたカードが入ったものをもってくる。
この箱の中の\(\small{ \ n \ }\)が書かれたカードと箱と箱の中が同じ数のカードを取り替える。そうすると箱の番号と箱の中のカードの数が同じであるものは一つもない。つまり完全順列になるよね。
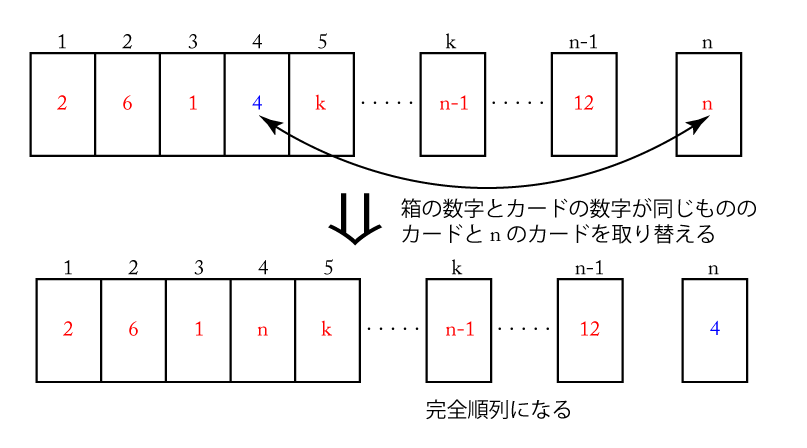
このように\(\small{ \ n \ }\)の箱の中の\(\small{ \ n \ }\)が書かれたカードと、箱と箱の中のカードの数が同じ数を入れ替えた完全順列の数は、箱と箱の中の数が同じものであるパターンが\(\small{ \ 1 \ }\)~\(\small{ \ n-1 \ }\)までの\(\small{ \ n-1 \ }\)通りあるから全部で\(\small{ \ (n-1)\times W(n-2) \ }\)通りある。
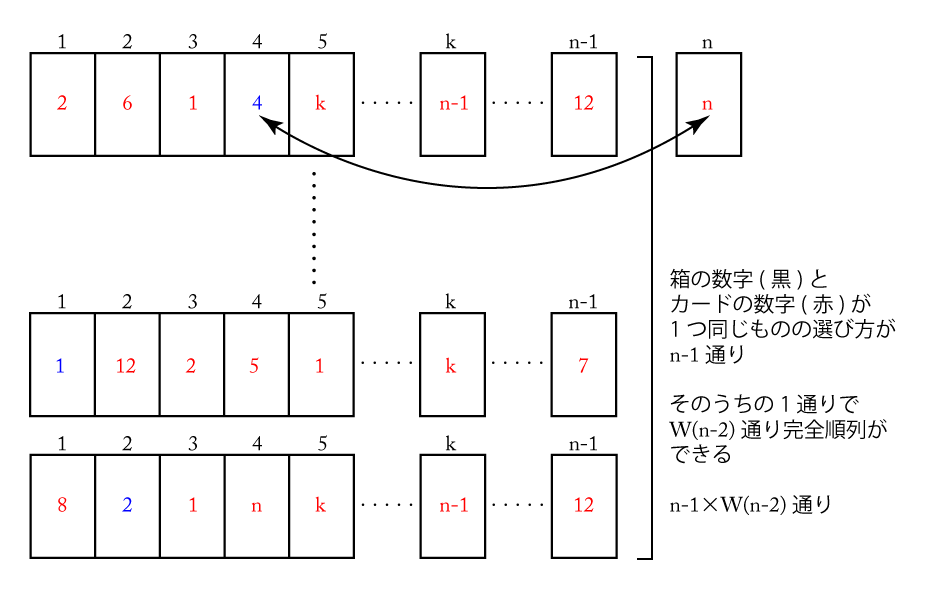
箱と中のカードの数が2つ以上同じものがある
次に\(\small{ \ 1 \ }\)から\(\small{ \ n-1 \ }\)までの\(\small{ \ n-1 \ }\)個の箱の中に\(\small{ \ 2 \ }\)つ以上、箱の番号と同じ番号のカードが入っている場合について考えてみよう。さっきと同じように、ここに\(\small{ \ n \ }\)の箱に\(\small{ \ n \ }\)が書かれたカードが入ったものをもってくる。
この箱の中の\(\small{ \ n \ }\)のカードと箱と箱の中のカードに書かれた数が同じ数のものを取り替えても、箱と箱の中の数が同じであるものが二つ以上あるため、完全順列にはならない。
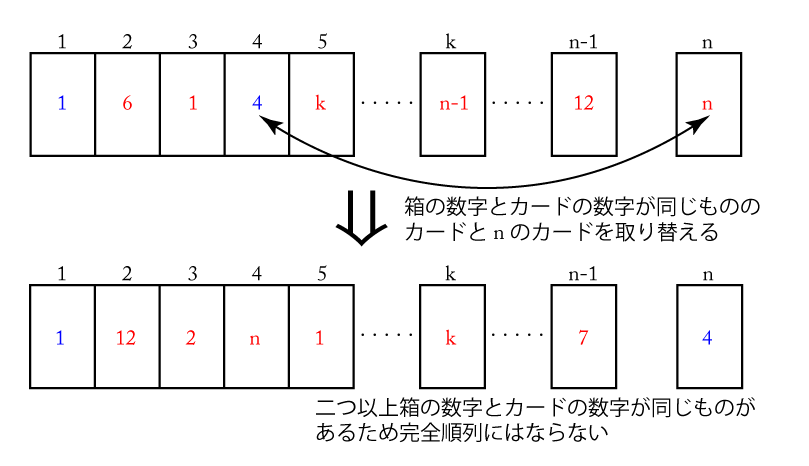
だから箱の番号と箱の中のカードに書かれた数が同じであるものが\(\small{ \ 2 \ }\)つ以上ある場合は、\(\small{ \ n \ }\)の箱に\(\small{ \ n \ }\)が書かれたカードが入ったものを持ってきて一度だけ取り替えても完全順列にはならないんだ。
漸化式を解く
上のことから
が言えるよね。
この漸化式から一般項を求めてみよう。
漸化式を変形すると
\(\small{ \ a_n=W(n+1)-(n+1)W(n) \ }\)とすると
\(\small{ \ a_{n+1}=-a_n \ }\)
※本当なら\(\small{ \ a_{n-1}=-a_{n-2} \ }\)だけど、計算しやすくするために\(\small{ \ a_{n+1}=-a_n \ }\)って\(\small{ \ n \ }\)を置き換えてるからね。
\(\small{ \ a_1=W(2)-2W(1)=2-2\times 0=1 \ }\)
\(\small{ \ a_n=(-1)^{n-1} \ }\)
\(\small{ \ W(n+1)-(n+1)W(n)=(-1)^{n-1} \ }\)とすると
両辺を\(\small{ \ (n+1)! \ }\)で割ると
\(\small{ \ \displaystyle\frac{W(n+1)}{(n+1)!}-\displaystyle\frac{W(n)}{n!}=\displaystyle\frac{(-1)^{n+1}}{(n+1)!} \ }\)
\(\small{ \ \displaystyle\frac{W(n)}{n!}=b_n \ }\)とすると
\(\small{ \ b_{n+1}-b_n=\displaystyle\frac{(-1)^{n+1}}{(n+1)!} \ }\)
\(\small{ \ b_n=b_1+\displaystyle \sum_{ k = 1 }^{ n-1 }\displaystyle\frac{(-1)^{k+1}}{(k+1)!} \ }\)
\(\small{ \ \ \ \ \ =b_1+\displaystyle \sum_{ k = 2 }^{ n }\displaystyle\frac{(-1)^k}{k!} \ }\)
\(\small{ \ b_1=0 \ }\)より
\(\small{ \ b_n=\displaystyle \sum_{ k = 2 }^{ n }\displaystyle\frac{(-1)^k}{k!} \ }\)
\(\small{ \ \displaystyle\frac{W(n)}{n!}=\displaystyle \sum_{ k = 2 }^{ n }\displaystyle\frac{(-1)^k}{k!} \ }\)
\(\small{ \ W(n)=n!\displaystyle \sum_{ k = 2 }^{ n }\displaystyle\frac{(-1)^k}{k!} \ }\)
\(\small{ \ 5 \ }\)人に招待状を送るため、宛名の書いた招待状とそれを入れる宛名を書いた封筒を作成した。招待状を全部間違った封筒に入れる方法は何通りあるか。
\(\small{ \ 5 \ }\)人がプレゼントを\(\small{ \ 1 \ }\)人\(\small{ \ 1 \ }\)個もちよってプレゼント交換する。このとき、全員が自分のプレゼントが当たらない交換の仕方は何通りあるか。
\(\small{\begin{eqnarray} \ W(5)&=&5!\displaystyle \sum_{ k = 2 }^{ 5}\displaystyle\frac{(-1)^k}{k!}\\
&=&120\left(\displaystyle\frac{1}{2!}-\displaystyle\frac{1}{3!}+\displaystyle\frac{1}{4!}-\displaystyle\frac{1}{5!}\right)\\
&=&44 \ \end{eqnarray}}\)
別解
\(\small{ \ 1 \ }\)番目が\(\small{ \ 2 \ }\)のときについて考えると

\(\small{ \ 1 \ }\)番目が\(\small{ \ 3、4、5 \ }\)のときも条件を満たす順列は同様に\(\small{ \ 11 \ }\)通りずつある。
よって求める答えは\(\small{ \ 11\times 4=44 \ }\)

Point 完全順列
①完全順列の攻略の手順を覚えよう

