こんにちは、リンス(@Lins016)です。
今回は重複順列について学習していこう。
重複順列
重複順列とは字の表すとおり、異なるものから重複を許していくつかを並べる順列のことで、異なる\(\small{ \ n \ }\)個の中から重複を許して\(\small{ \ r \ }\)個取り出して並べる重複順列の数は\(\small{ \ n\times n\times n\cdots\times n=n^r \ }\)になる。
重複を許さずに異なる\(\small{ \ n \ }\)個の中から\(\small{ \ r \ }\)個取り出して並べる順列の数は\(\small{ \ {}_n\mathrm{P}_r \ }\)だったよね。
ちなみに教科書には載ってないけど、重複順列の\(\small{ \ n^r \ }\)を記号で\(\small{ \ {}_n \prod_r \ }\)って書いたりもするから大学で数学が必要な人は知っておくといいよ。
重複順列
重複を許して\(\small{ \ n \ }\)個の中から
\(\small{ \ r \ }\)個取り出して並べる重複順列の数
\(\small{ \ {}_n \prod_r=n^r \ }\)
自然数を作る重複順列
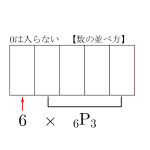
数を並べる順列で学習したように、重複を許して数を並べる重複順列でも、最高位の数は\(\small{ \ 0 \ }\)にならないように並べないといけない。この点に注意して問題を解こう。
合わせて重複を許さない問題についても復習しておこう。
-

順列と数字の並び方
全て異なる数字の並べ方で、条件のある問題や小さい順の順列の問題について解説しています。
続きを見る
\(\small{ \ 0,1,2,3,4 \ }\)の\(\small{ \ 5 \ }\)種類の数で作られる次のような数はいくつあるか答えよ。
(1)\(\small{ \ 5 \ }\)桁の自然数
(2)\(\small{ \ 5 \ }\)桁以下の自然数
(3)\(\small{ \ 5 \ }\)桁の自然数で偶数
(4)\(\small{ \ 123 \ }\)より小さい自然数
(1)最高位には\(\small{ \ 1~4 \ }\)が、それ以外の位には\(\small{ \ 0~4 \ }\)が入るので
\(\small{ \ 4\times5\times5\times5\times5=2500 \ }\)
(2)(1)と同様に4桁の自然数は
\(\small{ \ 4\times5\times5\times5=500 \ }\)
\(\small{ \ 3 \ }\)桁の自然数は
\(\small{ \ 4\times5\times5=100 \ }\)
\(\small{ \ 2 \ }\)桁の自然数は
\(\small{ \ 4\times5=20 \ }\)
\(\small{ \ 1 \ }\)桁の自然数は
\(\small{ \ 4 \ }\)
よって求める総数は
\(\small{ \ 2500+500+100+20+4=3124 \ }\)
(3)下一桁は\(\small{ \ 0,2,4 \ }\)だから
\(\small{ \ 4\times5\times5\times5\times3=1500 \ }\)
(4)\(\small{ \ 123 \ }\)より小さい\(\small{ \ 3 \ }\)桁の自然数は
\(\small{ \ 120 \ }\)台が\(\small{ \ 120 \ }\)~\(\small{ \ 122 \ }\)までの\(\small{ \ 3 \ }\)通り
\(\small{ \ 100 \ }\)~\(\small{ \ 110 \ }\)台は\(\small{ \ 1\times2\times5=10 \ }\)
\(\small{ \ 2 \ }\)桁の数は\(\small{ \ 4\times5=20 \ }\)
\(\small{ \ 1 \ }\)桁の数は\(\small{ \ 4 \ }\)
よって求める数は\(\small{ \ 3+10+20+4=37 \ }\)

-

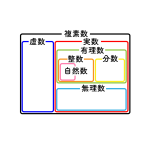
数の分類
複素数、実数、虚数、有理数、無理数、自然数などについて詳しく解説しています。
続きを見る
人をグループに分ける重複順列(部屋割り)
今度は人をグループに分ける分け方について考えてみよう。
例えば\(\small{ \ 10 \ }\)人を二つのグループ\(\small{ \ \mathrm{A} \ }\)と\(\small{ \ \mathrm{B} \ }\)に分けるとき、\(\small{ \ \mathrm{A} \ }\)と\(\small{ \ \mathrm{B} \ }\)の人数が違ってもOKとすると、その分け方は\(\small{ \ 2^{10}-2=1022 \ }\)通りある。
これはそれぞれの人\(\small{ \ 10 \ }\)名が\(\small{ \ \mathrm{A} \ }\)と\(\small{ \ \mathrm{B} \ }\)どちらかのグループに入るかって考えると
\(\small{ \ 2\times2\times2\times\cdots\times2=1024 \ }\)通りになる。
だけど、全員が\(\small{ \ \mathrm{A} \ }\)に入る場合と全員が\(\small{ \ \mathrm{B} \ }\)に入る場合は二つのグループに分かれてないから、この\(\small{ \ 2 \ }\)通りを除いた\(\small{ \ 2^{10}-2=1022 \ }\)通りになるんだ。
ちなみにこれって次の考え方もできるから覚えておこう。
\(\small{ \ 10 \ }\)人の中から\(\small{ \ \mathrm{A} \ }\)に入る人を\(\small{ \ 1 \ }\)人選ぶと\(\small{ \ {}_{10}\mathrm{C}_1 \ }\)通り。
もちろん残った\(\small{ \ 9 \ }\)人は全員\(\small{ \ \mathrm{B} \ }\)に入るからね。
\(\small{ \ 10 \ }\)人の中から\(\small{ \ \mathrm{A} \ }\)に入る人を\(\small{ \ 2 \ }\)人選ぶと\(\small{ \ {}_{10}\mathrm{C}_2 \ }\)通り。
\(\small{ \ 10 \ }\)人の中から\(\small{ \ \mathrm{A} \ }\)に入る人を\(\small{ \ 3 \ }\)人選ぶと\(\small{ \ {}_{10}\mathrm{C}_3 \ }\)通り。
\(\small{ \ 10 \ }\)人の中から\(\small{ \ \mathrm{A} \ }\)に入る人を\(\small{ \ 4 \ }\)人選ぶと\(\small{ \ {}_{10}\mathrm{C}_4 \ }\)通り。
\(\small{ \ \vdots \ }\)
\(\small{ \ 10 \ }\)人の中から\(\small{ \ \mathrm{A} \ }\)に入る人を\(\small{ \ 9 \ }\)人選ぶと\(\small{ \ {}_{10}\mathrm{C}_9 \ }\)通り。
つまり\(\small{ \ {}_{10}\mathrm{C}_1+{}_{10}\mathrm{C}_2+\cdots+{}_{10}\mathrm{C}_9 \ }\)通りが\(\small{ \ 10 \ }\)人を二つのグループ\(\small{ \ \mathrm{A} \ }\)と\(\small{ \ \mathrm{B} \ }\)に分ける総数になるよね。
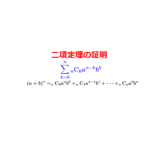
ここで二項定理
に\(\small{ \ n=10,a=1,b=1 \ }\)を代入すると
\(\small{ \ (1+1)^{10}={}_{10}\mathrm{C}_0+{}_{10}\mathrm{C}_1+{}_{10}\mathrm{C}_2+\cdots+{}_{10}\mathrm{C}_{10} \ }\)
\(\small{ \ {}_{10}\mathrm{C}_0={}_{10}\mathrm{C}_{10}=1 \ }\)だから
\(\small{ \ {}_{10}\mathrm{C}_1+{}_{10}\mathrm{C}_2+\cdots+{}_{10}\mathrm{C}_9=2^{10}-2 \ }\)になるよね。
つまり組合せを利用して考えても同じ答えが求まるんだ。求めるものが同じだから当たり前だよね。
よく解答と違うからって考える人がいるけど、組合せを使って答えても正解だからね。
でも二項定理知らずにコンビネーションの和を計算するのってかなり大変だよね。
だから組合せじゃなくて重複順列を利用して簡単に答えを出せるようにしておこう!
ちなみにグループ名を\(\small{ \ \mathrm{A} \ }\)と\(\small{ \ \mathrm{B} \ }\)ってつけずに、ただ二組に分けるだけならこの\(\small{ \ 1022 \ }\)を\(\small{ \ 2! \ }\)で割ればいいからね。
-

二項定理の証明
数学的帰納法を用いた二項定理の証明について詳しく解説しています。
続きを見る
(1)\(\small{ \ 8 \ }\)人を\(\small{ \ 3 \ }\)つの部屋\(\small{ \ \mathrm{A, \ B, \ C} \ }\)に入れる方法は何通りあるか。ただし、\(\small{ \ 8 \ }\)人全員が同じ部屋に入ってもよいものとする。
(2)\(\small{ \ 8 \ }\)人を\(\small{ \ 3 \ }\)つの組\(\small{ \ \mathrm{A, \ B, \ C} \ }\)に分ける方法は何通りあるか。
(1)\(\small{ \ 3^8=6561 \ }\)通り
(2)(1)の答えから二つの部屋に全員が入る場合と一つの部屋に全員が入る場合を除けばよいから
\(\small{ \ 3^8-3(2^8-2)-3=5796 \ }\)通り
じゃんけんの出し方と重複順列
じゃんけんの出し方も重複順列で考えよう。
例えば\(\small{ \ 4 \ }\)人でじゃんけんする場合、それぞれの人は、グー・チョキ・パーの\(\small{ \ 3 \ }\)通りの出し方があるから、\(\small{ \ 4 \ }\)人でじゃんけんする場合の出し方のは一人目が\(\small{ \ 3 \ }\)通り、二人目も\(\small{ \ 3 \ }\)通り、・・・ってなるから
\(\small{ \ 3\times3\times3\times3=3^4 \ }\)通りになるよね。
つまり重複順列の考え方になるんだ。
ちなみにこのすべての出し方からあいこや勝ち負けが決まる場合について考えてみよう。
\(\small{ \ 3 \ }\)人や\(\small{ \ 4 \ }\)人ぐらいだといいけど、人数が増えていくとあいこを考えるのは難しいよね。
だってあいこは「全員同じものを出す」と「全員バラバラ」があるからね。
\(\small{ \ 10 \ }\)人でじゃんけんするとき、全員バラバラを考えると、グーが何人、パーが何人、チョキが何人って考えないといけなくてかなり計算が大変になるよね。
だからあいこを考えるんじゃなくて勝ち負けが決まる場合を考えよう。
あいこはすべての出し方から勝ち負けが決まる以外を考えたらいいからね。
ちなみに勝ち負けが決まるのはどういう時かというと、全員が二種類を出すときだよね。
つまりグーとパーだけやチョキとパーだけ、チョキとグーだけの\(\small{ \ 3 \ }\)通りあるから、\(\small{ \ n \ }\)人でじゃんけんをするときの勝ち負けが決まる出し方は
\(\small{ \ (2^n-2)\times3 \ }\)通りになるよね。
だからあいこはこれを全体から引けばいいから
\(\small{ \ 3^n-3(2^n-2) \ }\)になるからね。

Point 重複順列
①異なる\(\small{ \ n \ }\)個の中から重複を許して\(\small{ \ r \ }\)個並べるのは\(\small{ \ n^r \ }\)通り
②部屋割り・じゃんけんは重複順列で考える