こんにちは、リンス(@Lins016)です。
今回は最短距離(最短経路)と組み合わせについて学習していこう。
最短距離(最短経路)と組み合わせの問題
最短距離の問題は格子状の図形の線上を通り, 図形上の\(\small{ \ 2 \ }\)点を遠回りせずに通る場合の数を求める問題のこと。
簡単に言うと道順の場合の数を求める問題ってことになるからね。基本的な考え方から、応用問題まで考えていくから、きちんと理解していこう。
\(\small{ \ \mathrm{A} \ }\)から\(\small{ \ \mathrm{B} \ }\)に向かう最短経路の数
\(\small{ \ \displaystyle\frac{(縦の移動数+横の移動数)!}{(縦の移動数)!(横の移動数)!} \ }\)
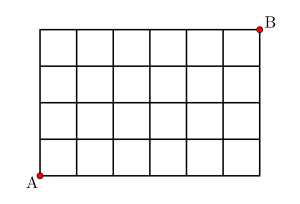
最短距離(最短経路)数の求め方
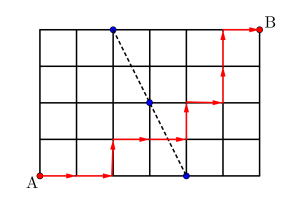
図のように\(\small{ \ \mathrm{A} \ }\)から\(\small{ \ \mathrm{B} \ }\)まで最短に進む場合が何通りあるか考えてみよう。
\(\small{ \ \mathrm{A} \ }\)から\(\small{ \ \mathrm{B} \ }\)に最短で行くためには右に\(\small{ \ 6 \ }\)回、上に\(\small{ \ 4 \ }\)回移動する必要があるから、
→→→→→→↑↑↑↑の並び方が、その最短経路の数になるんだ。
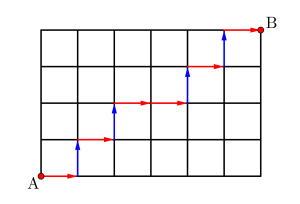
この矢印の並べ方は、同じものを含む順列になるから\(\small{ \ \displaystyle\frac{10!}{6!4!} \ }\)(または\(\small{ \ {}_{10}\mathrm{C}_6 \ }\))になるからね。
同じものを含む順列を忘れている人は再度確認しておこう。
つまり最短経路の数は縦の移動数と横の移動を調べて、
\(\small{ \ \displaystyle\frac{(縦の移動数+横の移動数)!}{(縦の移動数)!(横の移動数)!} \ }\)を計算すれば求まるんだ。
ある点を通る最短経路の数
次にある点を通る最短経路の数について考えてみよう。
図のように\(\small{ \ \mathrm{A} \ }\)から\(\small{ \ \mathrm{B} \ }\)に向かう最短経路のうち\(\small{ \ \mathrm{P, \ Q} \ }\)を通るものって条件を付けてみよう。
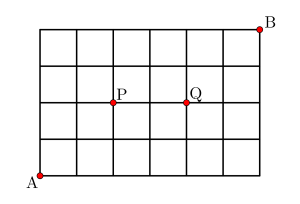
\(\small{ \ \mathrm{P, \ Q} \ }\)を通るためには、\(\small{ \ \mathrm{A} \ }\)から\(\small{ \ \mathrm{P} \ }\)に向かう最短経路の数と\(\small{ \ \mathrm{P} \ }\)から\(\small{ \ \mathrm{Q} \ }\)に向かう最短経路の数、\(\small{ \ \mathrm{Q} \ }\)から\(\small{ \ \mathrm{B} \ }\)に向かう数の最短経路の数を求めて、ぞれぞれ掛けたらいいんだ。
\(\small{ \ \mathrm{A} \ }\)から\(\small{ \ \mathrm{P} \ }\)の最短経路の数は\(\small{ \ \displaystyle\frac{4!}{2!2!} \ }\)通り
\(\small{ \ \mathrm{P} \ }\)から\(\small{ \ \mathrm{Q} \ }\)の最短経路の数は\(\small{ \ 1 \ }\)通り
\(\small{ \ \mathrm{Q} \ }\)から\(\small{ \ \mathrm{B} \ }\)の最短経路の数は\(\small{ \ \displaystyle\frac{4!}{2!2!} \ }\)通り
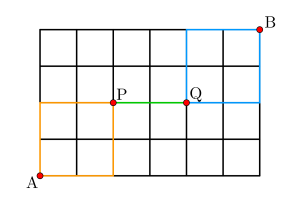
よって求める最短経路の数は\(\small{ \ \displaystyle\frac{4!}{2!2!}\times 1 \times \displaystyle\frac{4!}{2!2!}=36 \ }\)通り
だから、ある点を通るって言われたらその点までの最短経路数とその点から次の点までの最短経路数をかければいいからね。
通れない経路がある最短経路の数
次は図のように×印の部分が通行不可になっている場合の最短経路を求めてみよう。
この通行不可の問題は
通行不可となっている部分を通る最短経路数を求めて、それを全事象から引いて求めるんだ。
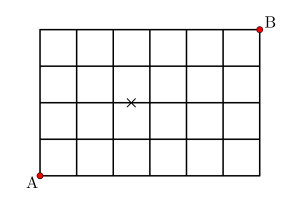
つまり余事象を利用するってことね。
\(\small{ \ \mathrm{A} \ }\)から\(\small{ \ \mathrm{B} \ }\)の最短経路数は\(\small{ \ \displaystyle\frac{10!}{6!4!} \ }\)通り
\(\small{ \ \mathrm{A} \ }\)から\(\small{ \ \mathrm{P} \ }\)の最短経路数は\(\small{ \ \displaystyle\frac{4!}{2!2!} \ }\)通り
\(\small{ \ \mathrm{P} \ }\)から\(\small{ \ \mathrm{R} \ }\)の最短経路数は\(\small{ \ 1 \ }\)通り
\(\small{ \ \mathrm{R} \ }\)から\(\small{ \ \mathrm{B} \ }\)の最短経路数は\(\small{ \ \displaystyle\frac{5!}{3!2!} \ }\)通り
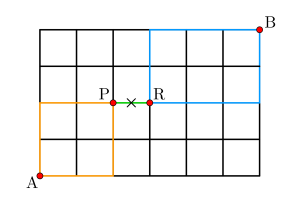
よって求める最短経路数は\(\small{ \ \displaystyle\frac{10!}{6!4!}-\displaystyle\frac{4!}{2!2!}\times 1 \times \displaystyle\frac{5!}{3!2!}=150 \ }\)通り
通行不可の問題は、余事象を利用して考えよう。
池のある最短経路の数
次に図のような池がある最短経路の問題を考えてみよう。
当然池を通ることはできないから、池を避けて\(\small{ \ \mathrm{A} \ }\)から\(\small{ \ \mathrm{B} \ }\)に向かわないといけないからね。

この池を通る問題を考えるまえに知っておいてほしいことが一つあるんだ。
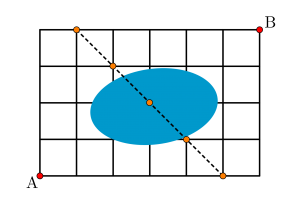
それは図のオレンジの点を通らずに\(\small{ \ \mathrm{A} \ }\)から\(\small{ \ \mathrm{B} \ }\)に行くことはできないってこと。
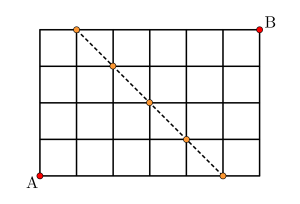
つまり\(\small{ \ \mathrm{A} \ }\)と\(\small{ \ \mathrm{B} \ }\)分割するように直線を引いたとき、その直線が交わる格子点を通らずに\(\small{ \ \mathrm{A} \ }\)から\(\small{ \ \mathrm{B} \ }\)に行くことはできないんだ。
ただし、注意しないといけなこともある。次の図を見てみよう。

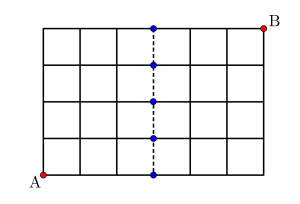
\(\small{ \ \mathrm{A} \ }\)と\(\small{ \ \mathrm{B} \ }\)分割するように直線を引いたけど、この分割する直線が格子の辺と交わるものはダメなんだ。
図のように点をすり抜けて通ることが可能になるからね。
だから分割する直線は\(\small{ \ 1 \ }\)つの格子の対角線か辺の延長じゃないといけない。
さあこれを頭にいれてもう一度池の問題を考えてみよう。
オレンジの一つ一つの点について考えてみよう。
①一番下のオレンジの点

\(\small{ \ \mathrm{A} \ }\)→オレンジ→\(\small{ \ \mathrm{B} \ }\)の順
\(\small{ \ 1\times \displaystyle\frac{5!}{1!4!}=5 \ }\)通り
②下から二番目のオレンジの点
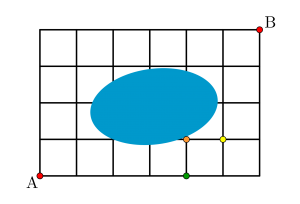
\(\small{ \ \mathrm{A} \ }\)→緑→オレンジ→黄→\(\small{ \ \mathrm{B} \ }\)の順
\(\small{ \ 1\times1\times1\times\displaystyle\frac{4!}{1!3!}=4 \ }\)通り
③下から三番目のオレンジの点

池の中は通らない
\(\small{ \ \therefore 0 \ }\)通り
④下から四番目のオレンジの点
\(\small{ \ \mathrm{A} \ }\)→青→オレンジ→\(\small{ \ \mathrm{B} \ }\)の順
\(\small{ \ \displaystyle\frac{4!}{1!3!}\times1\times\displaystyle\frac{5!}{4!1!}=20 \ }\)通り
⑤一番上のオレンジの点

\(\small{ \ \mathrm{A} \ }\)→オレンジ→\(\small{ \ \mathrm{B} \ }\)の順
\(\small{ \ \displaystyle\frac{5!}{1!4!}\times 1=5 \ }\)通り
よって求める最短経路の数は
\(\small{ \ 5+4+20+5=34 \ }\)通り
今回考えた各オレンジの点じゃなくて、\(\small{ \ \mathrm{A} \ }\)と\(\small{ \ \mathrm{B} \ }\)分割する別の直線上の点でも構わない。池の形によってどの対角線や辺の延長の直線の場合の計算が楽になるか考えてから問題を解くようにしよう。

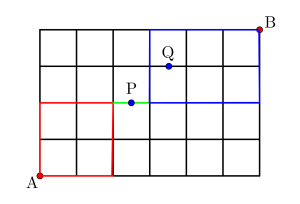
図のように道路が格子状になった町がある。\(\small{ \ \mathrm{A} \ }\)から\(\small{ \ \mathrm{B} \ }\)までの長さが最短の道で行くとき、\(\small{ \ \mathrm{P} \ }\)と\(\small{ \ \mathrm{Q} \ }\)を通らずに行く道順は何通りあるか求めよ。
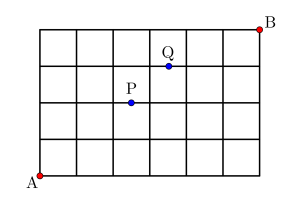
\(\small{ \ \mathrm{A} \ }\)から\(\small{ \ \mathrm{B} \ }\)へ行く全ての道順は\(\small{ \ \displaystyle\frac{10!}{6!4!}=210 \ }\)通り
\(\small{ \ \mathrm{A} \ }\)から\(\small{ \ \mathrm{P} \ }\)を通って\(\small{ \ \mathrm{B} \ }\)へ行く道順は
\(\small{ \ \displaystyle\frac{4!}{2!2!}\times 1 \times \displaystyle\frac{5!}{3!2!}=60 \ }\)通り
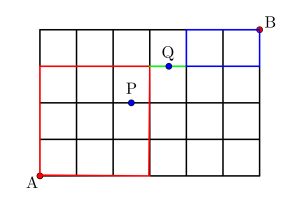
\(\small{ \ \mathrm{A} \ }\)から\(\small{ \ \mathrm{Q} \ }\)を通って\(\small{ \ \mathrm{B} \ }\)へ行く道順は
\(\small{ \ \displaystyle\frac{6!}{3!3!}\times 1 \times \displaystyle\frac{3!}{2!1!}=60 \ }\)通り
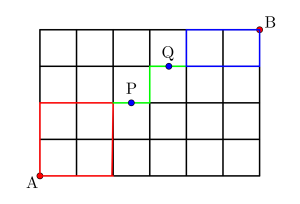
\(\small{ \ \mathrm{A} \ }\)から\(\small{ \ \mathrm{P} \ }\)と\(\small{ \ \mathrm{Q} \ }\)を通って\(\small{ \ \mathrm{B} \ }\)へ行く道順は
\(\small{ \ \displaystyle\frac{4!}{2!2!}\times 1 \times \displaystyle\frac{3!}{2!1!}=18 \ }\)通り
よって\(\small{ \ \mathrm{P} \ }\)と\(\small{ \ \mathrm{Q} \ }\)を通らずに行く道順は
\(\small{ \ 210-60-60+18=108 \ }\)通り

Point 最短距離(最短経路)と組み合わせ
①横の移動、縦の移動の個数を調べる
②通行負荷は余事象を利用する
③ある点までの個数と次の点までの個数を掛けて経路を求める

