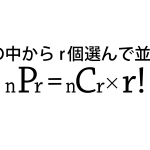こんにちは、リンス(@Lins016)です。
今回は確率の基本について学習していこう。
事象と確率
事象っていうのは「ある試行の結果として起こる事柄」のことで、「ある試行において起こりうる個々の場合の事象」のことを根元事象っていう。
例えばコインを\(\small{ \ 1 \ }\)枚投げる場合、「表が出る」「裏が出る」が根元事象になる。
さらにこの根元事象全体からなる集合で表される事象のことを全事象っていうからね。
確率の定義
全事象\(\small{ \ \mathrm{U} \ }\)の根本事象の起こり方がどれも同様に確からしいとき
事象\(\small{ \ \mathrm{A} \ }\)の起こる確率
\(\small{ \ P(\mathrm{A})=\displaystyle\frac{n(\mathrm{A})}{n(\mathrm{U})} \ }\)
\(\small{ \ n(\mathrm{A}) \ }\)は\(\small{ \ \mathrm{A} \ }\)の起こる場合の数
\(\small{ \ n(\mathrm{U}) \ }\)は起こりうるすべての場合の数
確率の定義
例えばサイコロを投げるとき、\(\small{ \ 1 \ }\)の目が出る確率は\(\small{ \ 1/6 \ }\)って教わったよね。
もちろん高校数学ではこれが当たり前なんだけど、それは「サイコロの目の出方はどれも同様に確からしい」ってことが前提なんだ。
立方体じゃないサイコロや重心が少しずれたサイコロがあるとしたら、「サイコロの目の出方はどれも同様に確からしい」とはいえなくなるから、\(\small{ \ 1 \ }\)の目が出る確率は\(\small{ \ 1/6 \ }\)とは限らないんだ。
事象\(\small{ \ \mathrm{A} \ }\)が起こる確率を求めるとき、
\(\small{ \ P(\mathrm{A})=\displaystyle\frac{n(\mathrm{A})}{n(\mathrm{U})} \ }\)
\(\small{ \ n(\mathrm{A}) \ }\)は\(\small{ \ \mathrm{A} \ }\)の起こる場合の数
\(\small{ \ n(\mathrm{U}) \ }\)は起こりうるすべての場合の数
を計算するよね。でもこの式を利用するなら、「全事象\(\small{ \ \mathrm{U} \ }\)の根本事象の起こり方がどれも同様に確からしい」ってことが必要になるんだ。
それを分かった上で「サイコロを投げて、\(\small{ \ 1 \ }\)の目が出る確率は\(\small{ \ 1/6 \ }\)」や「コインを投げて、表が出る確率は\(\small{ \ 1/2 \ }\)」って理解しておこう。
\(\small{ \ \mathrm{A} \ }\)さんと\(\small{ \ \mathrm{B} \ }\)さんと\(\small{ \ \mathrm{C} \ }\)さんが\(\small{ \ 3 \ }\)人でジャンケンをするとき、\(\small{ \ 1 \ }\)人だけ勝つ確率を求めよ。
\(\small{ \ 1 \ }\)人のジャンケンの出し方は\(\small{ \ 3 \ }\)通りだから\(\small{ \ 3 \ }\)人のジャンケンの出し方\(\small{ \ 3^3 \ }\)通り
\(\small{ \ 1 \ }\)人が勝つジャンケンの出し方は
(グー、チョキ、チョキ)、(チョキ、パー、パー)、(パー、グー、グー)の\(\small{ \ 3 \ }\)通り
勝つ人の選び方は\(\small{ \ \mathrm{A、B、C} \ }\)の\(\small{ \ 3 \ }\)通り
よって求める確率は
\(\small{ \ \displaystyle\frac{3\times3}{3^3}=\displaystyle\frac{1}{3} \ }\)
\(\small{ \ \mathrm{A} \ }\)さんがグーで勝つ確率は
\(\small{ \ \mathrm{A} \ }\)さんがグーを出す確率×\(\small{ \ \mathrm{B} \ }\)さんがチョキを出す確率×\(\small{ \ \mathrm{C} \ }\)さんがチョキを出す確率より
\(\small{ \ \displaystyle\frac{1}{3}\times\displaystyle\frac{1}{3}\times\displaystyle\frac{1}{3}=\displaystyle\frac{1}{9} \ }\)
\(\small{ \ \mathrm{A} \ }\)さんの勝ち方はグー、チョキ、パーの\(\small{ \ {}_3\mathrm{C}_1 \ }\)通り
勝つ人の選び方は\(\small{ \ 3 \ }\)人の中から\(\small{ \ 1 \ }\)人選ぶから\(\small{ \ {}_3\mathrm{C}_1 \ }\)通り
よって求める確率は
\(\small{ \ \displaystyle\frac{1}{3}\times\displaystyle\frac{1}{3}\times\displaystyle\frac{1}{3}\times{}_3\mathrm{C}_1\times{}_3\mathrm{C}_1=\displaystyle\frac{1}{3} \ }\)

解答1では事象\(\small{ \ \mathrm{A} \ }\)が起こる場合の数を求めて、全事象の場合の数で割って確率を求めて、解答2ではジャンケンをグーを出す確率\(\small{ \ 1/3 \ }\)を利用した。
確率を求めるのは、事象\(\small{ \ \mathrm{A} \ }\)が起こる場合の数を求めて、全事象の場合の数で割って確率を求めればいいんだけど、「\(\small{ \ 1 \ }\)の目が出る確率は\(\small{ \ 1/6 \ }\)」とかの、あらかじめ分かっている確率の値を利用して(この確率を掛けたりして)確率を求める問題もある。
出題される問題は、この方法で解く問題も多い。でも実際やってることは同じことになるからね。
区別の付かないものを利用した確率
場合の数では区別のつかないサイコロや球の問題とかあるよね。
区別のつかないサイコロ\(\small{ \ 2 \ }\)個を投げる場合、全事象\(\small{ \ 36 \ }\)通りじゃなく、\(\small{ \ 21 \ }\)通りになるよね。でも場合の数だとそれでいいけど、確率を考えるときにはそうはいかない。
区別のつくサイコロ\(\small{ \ 36 \ }\)通り

区別のつかないサイコロ\(\small{ \ 21 \ }\)通り
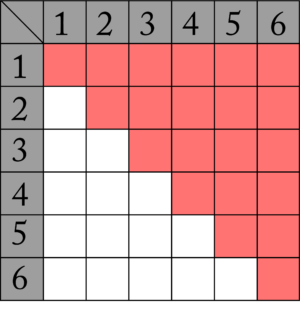
だって実際区別が付かないって言うのは見た目でわからないってだけで本当は\(\small{ \ 2 \ }\)個あるからね。
例えば、サイコロ\(\small{ \ 2 \ }\)個を投げて\(\small{ \ 1 \ }\)と\(\small{ \ 2 \ }\)が出る場合、区別がつかないと\(\small{ \ 1 \ }\)通りってなるけど、実際は別のものなんだから\(\small{ \ \mathrm{A} \ }\)のサイコロが\(\small{ \ 2 \ }\)で\(\small{ \ \mathrm{B} \ }\)のサイコロが\(\small{ \ 1 \ }\)の場合と、\(\small{ \ \mathrm{A} \ }\)のサイコロが\(\small{ \ 1 \ }\)で\(\small{ \ \mathrm{B} \ }\)のサイコロが\(\small{ \ 2 \ }\)の場合の\(\small{ \ 2 \ }\)通りあるよね。
でも\(\small{ \ 1 \ }\)と\(\small{ \ 1 \ }\)が出る場合、\(\small{ \ \mathrm{A} \ }\)のサイコロも\(\small{ \ \mathrm{B} \ }\)のサイコロも\(\small{ \ 1 \ }\)が出るときしかないから、区別がついてもつかなくても\(\small{ \ 1 \ }\)通りになるよね。つまり区別がつかないって考えたままだと、\(\small{ \ 1 \ }\)と\(\small{ \ 2 \ }\)が出る確率と\(\small{ \ 1 \ }\)と\(\small{ \ 1 \ }\)が出る確率が同様に確からしくないってことになるんだ。
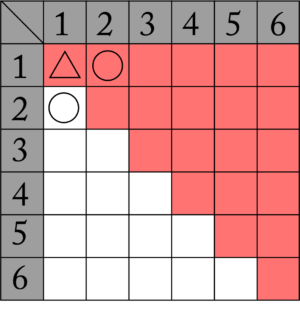
だから区別のつかないサイコロを投げる問題でも区別をつけないといけないんだ。
でも考えてみてほしい。区別がつかないサイコロにシャーペンで少し線を書くと、これってもう区別がつくサイコロになるよね。しかも線を書いたからといって出る確率がかわるわけでもないしね。
だから確率の問題を考えるとき区別が付かないものも、区別して考えて問題ないんだ。本当は別のものだから、区別するのは当然だよね。
だから袋の中から球を取り出す問題の同じ色の球も区別して考えるからね。
\(\small{ \ \mathrm{KAKUYASU} \ }\)という\(\small{ \ 8 \ }\)文字がある。次の問いに答えよ。
(1)\(\small{ \ 8 \ }\)文字を\(\small{ \ 1 \ }\)列に並べるとき、両端が\(\small{ \ \mathrm{A} \ }\)になる確率を求めよ。
(2)\(\small{ \ 8 \ }\)文字の中から\(\small{ \ 4 \ }\)文字をとって\(\small{ \ 1 \ }\)列に並べるとき、その\(\small{ \ 4\ }\)文字が母音である確率を求めよ。
\(\small{ \ \mathrm{ K_1A_1K_2U_1YA_2SU_2} \ }\)と各文字を区別する
(1)
\(\small{ \ 1 \ }\)列に並べるのは\(\small{ \ 8! \ }\)
両端が\(\small{ \ \mathrm{A} \ }\)になるのは\(\small{ \ 6!\times2 \ }\)
よって求める確率は\(\small{ \ \displaystyle\frac{6!\times2}{8!}= \displaystyle\frac{1}{28} \ }\)
(2)
\(\small{ \ 4 \ }\)つの文字をとって\(\small{ \ 1 \ }\)列に並べるのは\(\small{ \ {}_8\mathrm{P}_4 \ }\)
母音を\(\small{ \ 4 \ }\)つとって\(\small{ \ 1 \ }\)列に並べるのは\(\small{ \ {}_4\mathrm{P}_4 \ }\)
よって求める確率は
\(\small{ \ \displaystyle\frac{{}_4\mathrm{P}_4}{ {}_8\mathrm{P}_4 }= \displaystyle\frac{1}{70} \ }\)

全部の並べ方が\(\small{ \ \displaystyle\frac{8!}{2!2!2!} \ }\)
両端が\(\small{ \ \mathrm{A} \ }\)になる並べ方は\(\small{ \ \displaystyle\frac{6!}{2!2!} \ }\)
これらは同様に確からしいから
\(\small{ \ \displaystyle\frac{6!}{2!2!}\div\displaystyle\frac{8!}{2!2!2!}=\displaystyle\frac{6!2!}{8!}=\displaystyle\frac{1}{28} \ }\)って同じになる。
さっき話したサイコロ\(\small{ \ 2 \ }\)個の場合、区別が付かないって考えだと、\(\small{ \ 1 \ }\)と\(\small{ \ 2 \ }\)が出る確率と\(\small{ \ 1 \ }\)と\(\small{ \ 1 \ }\)が出る確率が同様に確からしくないってことだったけど、\(\small{ \ \mathrm{KAKUYASU} \ }\)の場合は区別しなくても同様に確からしい。
というのも区別しない\(\small{ \ \mathrm{KAKUYASU} \ }\)の並べ方は\(\small{ \ 1 \ }\)通りだよね。
この並べ方を区別した\(\small{ \ \mathrm{ K_1A_1K_2U_1YA_2SU_2} \ }\)で考えると、\(\small{ \ \mathrm{A_1A_2} \ }\)の入れ替え、\(\small{ \ \mathrm{K_1K_2} \ }\)の入れ替え、\(\small{ \ \mathrm{U_1U_2} \ }\)の入れ替えがあるから\(\small{ \ 2^3 \ }\)通りある。
ただ、これは区別しないどの並べ方\(\small{ \ 1 \ }\)通りに対しても、区別した並べ方は\(\small{ \ 2^3 \ }\)通りあるから、区別しないどの並べ方も同様に確からしいことになるんだ。
だから区別しなくて解いても問題ないんだけど、(2)は区別しないままだと計算がかなりめんどくさい。区別しないまま解ける問題もあるけど、区別した方が楽に解ける問題が多いってことを覚えておこう。
PとCの使い方
確率を場合の数を利用して求めるときに、とても大切になるのが順列\(\small{ \ \mathrm{P} \ }\)(permutation)を使うか、組み合わせ\(\small{ \ \mathrm{C} \ }\)(combination)を使うかってことになる。
順列を使うときは「選んで並べる」ときで、組み合わせを使うときは「選ぶ」ときだよね。ついつい順列でやりがちだけど、並べる必要がなかったら組み合わせで考えた方が計算も少ないからミスも減る。
問題文からどっちを使うのか意識して問題を解こう。
-

順列と組み合わせの違い
PやCの計算や使い方などについて解説しています。
続きを見る
袋の中にある赤玉\(\small{ \ 4 \ }\)個と白玉\(\small{ \ 5 \ }\)個から同時に\(\small{ \ 3 \ }\)個取り出すとき、\(\small{ \ 3 \ }\)個とも同じ色である確率を求めよ。
赤玉\(\small{ \ 3 \ }\)個取る確率は\(\small{ \ \displaystyle\frac{{}_4\mathrm{C}_3}{{}_9\mathrm{C}_3} \ }\)
白玉\(\small{ \ 3 \ }\)個取る確率は\(\small{ \ \displaystyle\frac{{}_5\mathrm{C}_3}{{}_9\mathrm{C}_3} \ }\)
これらは同時に起こらないから
\(\small{ \ \displaystyle\frac{{}_4\mathrm{C}_3}{{}_9\mathrm{C}_3}+\displaystyle\frac{{}_5\mathrm{C}_3}{{}_9\mathrm{C}_3}=\displaystyle\frac{1}{6} \ }\)
赤玉\(\small{ \ 3 \ }\)個取る確率は\(\small{ \ \displaystyle\frac{4}{9}\times\displaystyle\frac{3}{8}\times\displaystyle\frac{2}{7} \ }\)
白玉\(\small{ \ 3 \ }\)個取る確率は\(\small{ \ \displaystyle\frac{5}{9}\times\displaystyle\frac{4}{8}\times\displaystyle\frac{3}{7}} \)
これらは同時に起こらないから
\(\small{ \ \displaystyle\frac{4}{9}\times\displaystyle\frac{3}{8}\times\displaystyle\frac{2}{7}+\displaystyle\frac{5}{9}\times\displaystyle\frac{4}{8}\times\displaystyle\frac{3}{7}=\displaystyle\frac{1}{6} \ }\)

次に解答2だけど、赤玉を\(\small{ \ 3 \ }\)個取る計算を見てみると\(\small{ \ 1 \ }\)つ目を取るとき袋の中には全部で\(\small{ \ 9 \ }\)個玉があって、その中に\(\small{ \ 4 \ }\)個の赤玉があるから赤玉を取り出す確率は\(\small{ \ \displaystyle\frac{4}{9} \ }\)。
取り出した後その玉は元に戻さないから、袋の中は全部で残った\(\small{ \ 8 \ }\)個あって、その中には\(\small{ \ 3 \ }\)個の赤玉があるから\(\small{ \ 2 \ }\)つ目の赤玉を取り出す確率は\(\small{ \ \displaystyle\frac{3}{8} \ }\)。
同様に次に赤玉を取り出す確率は\(\small{ \ \displaystyle\frac{2}{7} \ }\)になるから、これらをかけて、赤玉\(\small{ \ 3 \ }\)個取る確率は\(\small{ \ \displaystyle\frac{4}{9}\times\displaystyle\frac{3}{8}\times\displaystyle\frac{2}{7} \ }\)になるんだ。
実はこの計算って\(\small{ \ \displaystyle\frac{{}_4\mathrm{P}_3}{{}_9\mathrm{P}_3} \ }\)の計算と同じだからね。
つまり\(\small{ \ 1 \ }\)個ずつ取り出して並べたってことになるよね。答えは間違ってるわけじゃないけど、同時に取り出すなら\(\small{ \ \mathrm{P} \ }\)より\(\small{ \ \mathrm{C} \ }\)を使いたいよね。
普段から意識して\(\small{ \ \mathrm{P} \ }\) と\(\small{ \ \mathrm{C} \ }\)を使い分けよう。
Point 確率の基本
①Aの起こる確率はAの事象/全事象
②区別つかないものは区別して考えると楽に解けることが多い
③順列と組み合わせの違いをきちんと利用する