こんにちは、リンス(@Lins016)です。
今回は複素数と図形(直線の応用)について学習していこう。
複素数平面上の図形
複素数平面上の図形の第3回目は直線の応用について学習していこう。第1回で直線を学習したけど、その直線は垂直二等分線と実軸や虚軸に平行な直線だけだったからね。
-

複素数と図形(直線)
複素数平面に描かれる直線の方程式について詳しく解説しています。
続きを見る
今回は他の直線についても学習していこう。
点\(\small{ \ \mathrm{A}\left(\alpha\right) \ }\)、点\(\small{ \ \mathrm{B}\left(\beta\right) \ }\)、点\(\small{ \ \mathrm{C}\left(\gamma\right) \ }\)、点\(\small{ \ \mathrm{D}\left(\sigma\right) \ }\)において
\(\small{ \ \mathrm{AB /\!/ CD} \ }\)のとき
\(\small{ \ \displaystyle\frac{\sigma-\gamma}{\beta-\alpha}=\overline{\left(\displaystyle\frac{\sigma-\gamma}{\beta-\alpha}\right)} \ }\)
\(\small{ \ \mathrm{AB \perp CD} \ }\)のとき
\(\small{ \ \displaystyle\frac{\sigma-\gamma}{\beta-\alpha}+\overline{\left(\displaystyle\frac{\sigma-\gamma}{\beta-\alpha}\right)}=0 \ }\)
平行を表す複素数
点\(\small{ \ \mathrm{A}\left(\alpha\right) \ }\)、点\(\small{ \ \mathrm{B}\left(\beta\right) \ }\)、点\(\small{ \ \mathrm{C}\left(\gamma\right) \ }\)、点\(\small{ \ \mathrm{D}\left(\sigma\right) \ }\)が\(\small{ \ \mathrm{AB /\!/ CD} \ }\)を満たす場合について考えてみよう。
\(\small{ \ \beta-\alpha \ }\)を表す複素数は図のように点\(\small{ \ \mathrm{A}\left(\alpha\right) \ }\)を原点に移す平行移動によって点\(\small{ \ \mathrm{B}\left(\beta\right) \ }\)が移る点になる。この点を点\(\small{ \ \mathrm{E} \ }\)とすると、\(\small{ \ \mathrm{AB /\!/ OE} \ }\)が言えるよね。

同様に\(\small{ \ \sigma-\gamma \ }\)を表す複素数は点\(\small{ \ \mathrm{C}\left(\gamma\right) \ }\)を原点に移す平行移動によって点\(\small{ \ \mathrm{D}\left(\sigma\right) \ }\)が移る点になる。この点を点\(\small{ \ \mathrm{F} \ }\)とすると、\(\small{ \ \mathrm{CD /\!/ OF} \ }\)が言える。
だから\(\small{ \ \mathrm{AB /\!/ CD} \ }\)なら\(\small{ \ \mathrm{OE /\!/ OF} \ }\)になるよね。
原点\(\small{ \ 0、z_1、z_2 \ }\)が同一直線上にあるとき、\(\small{ \ z_2=kz_1 \ }\)になる実数\(\small{ \ k \ }\)が存在する。
\(\small{ \ \displaystyle\frac{z_2}{z_1}=k \ }\)より\(\small{ \ \displaystyle\frac{z_2}{z_1}=\overline{\left(\displaystyle\frac{z_2}{z_1}\right)} \ }\)
これを利用すると、\(\small{ \ \mathrm{AB /\!/ CD} \ }\)なら\(\small{ \ \sigma-\gamma=k(\beta-\alpha) \ }\)になる実数\(\small{ \ k \ }\)が存在する。
つまり\(\small{ \ \mathrm{AB /\!/ CD} \ }\)のとき\(\small{ \ \displaystyle\frac{\sigma-\gamma}{\beta-\alpha}=\overline{\left(\displaystyle\frac{\sigma-\gamma}{\beta-\alpha}\right)} \ }\)になるんだ。
垂直を表す複素数
次に点\(\small{ \ \mathrm{A}\left(\alpha\right) \ }\)、点\(\small{ \ \mathrm{B}\left(\beta\right) \ }\)、点\(\small{ \ \mathrm{C}\left(\gamma\right) \ }\)、点\(\small{ \ \mathrm{D}\left(\sigma\right) \ }\)が\(\small{ \ \mathrm{AB \perp CD} \ }\)を満たす場合について考えてみよう。
さっきと同じように\(\small{ \ \beta-\alpha \ }\)を表す複素数を点\(\small{ \ \mathrm{E} \ }\)、\(\small{ \ \sigma-\gamma \ }\)を表す複素数を点\(\small{ \ \mathrm{F} \ }\)とすると、\(\small{ \ \mathrm{AB /\!/ OE} \ }\)、\(\small{ \ \mathrm{CD /\!/ OF} \ }\)になるから、\(\small{ \ \mathrm{AB \perp CD} \ }\)なら\(\small{ \ \mathrm{OE \perp OF} \ }\)になるよね。

原点\(\small{ \ 0、z_1、z_2 \ }\)が垂直になるとき、\(\small{ \ \mathrm{arg}\displaystyle\frac{z_2-0}{z_1-0}=\mathrm{arg}\displaystyle\frac{z_2}{z_1}=\pm\displaystyle\frac{\pi}{2} \ }\)になる。
\(\small{ \ \displaystyle\frac{z_2}{z_1} \ }\)は純虚数になるから、\(\small{ \ \displaystyle\frac{z_2}{z_1}=ki \ }\)となる実数\(\small{ \ k \ }\)が存在し、\(\small{ \ \displaystyle\frac{z_2}{z_1}+\overline{\left(\displaystyle\frac{z_2}{z_1}\right)}=0 \ }\)になる。
これを利用すると\(\small{ \ \mathrm{AB \perp CD} \ }\)なら\(\small{ \ \sigma-\gamma=ki(\beta-\alpha) \ }\)になる実数\(\small{ \ k \ }\)が存在する。
つまり\(\small{ \ \mathrm{AB \perp CD} \ }\)のとき\(\small{ \ \displaystyle\frac{\sigma-\gamma}{\beta-\alpha}+\overline{\left(\displaystyle\frac{\sigma-\gamma}{\beta-\alpha}\right)}=0 \ }\)になるんだ。
直線への応用
平行と垂直な条件が分かったところで、これを直線に応用してみよう。
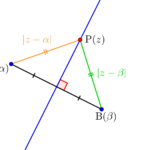
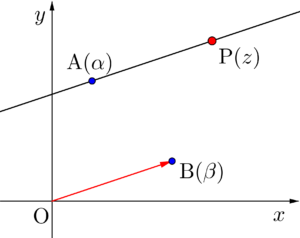
点\(\small{ \ \mathrm{A}(\alpha) \ }\)を通り、\(\small{ \ \mathrm{OB} \ }\)(点\(\small{ \ \mathrm{B}\left(\beta\right) \ }\))に平行な直線を描く\(\small{ \ \mathrm{P}\left(z\right) \ }\)の満たす方程式を考えてみよう。
\(\small{ \ \mathrm{AP} \ }\)と\(\small{ \ \mathrm{OB} \ }\)が平行になればいいから、
\(\small{ \ \displaystyle\frac{z-\alpha}{\beta}=\overline{\left(\displaystyle\frac{z-\alpha}{\beta}\right)} \ }\)
これを整理すると
\(\small{ \ \displaystyle\frac{z-\alpha}{\beta}=\left(\displaystyle\frac{\overline{z}-\overline{\alpha}}{\overline{\beta}}\right) \ }\)
\(\small{ \ \overline{\beta}(z-\alpha)=\beta\left(\overline{z}-\overline{\alpha}\right) \ }\)
\(\small{ \ \overline{\beta}z-\beta \overline{z}-\alpha\overline{\beta}+ \overline{\alpha}\beta=0 \ }\)
この\(\small{ \ \overline{\beta}z-\beta \overline{z}-\alpha\overline{\beta}+ \overline{\alpha}\beta=0 \ }\)が点\(\small{ \ \mathrm{A}(\alpha) \ }\)を通り、\(\small{ \ \mathrm{OB} \ }\)(点\(\small{ \ \mathrm{B}\left(\beta\right) \ }\))に平行な直線を描く\(\small{ \ \mathrm{P}\left(z\right) \ }\)の満たす方程式になるんだ。
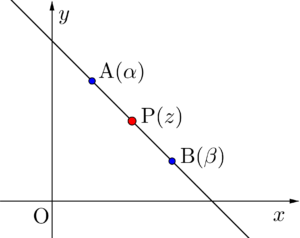
次に点\(\small{ \ \mathrm{A}(\alpha) \ }\)と点\(\small{ \ \mathrm{B}\left(\beta\right) \ }\)を通る直線を描く\(\small{ \ \mathrm{P}\left(z\right) \ }\)の満たす方程式を考えてみよう。
\(\small{ \ \mathrm{A、B、P} \ }\)が同一直線上にあるから
\(\small{ \ \displaystyle\frac{z-\alpha}{\beta-\alpha}=\overline{\left(\displaystyle\frac{z-\alpha}{\beta-\alpha}\right)} \ }\)
\(\small{ \ \displaystyle\frac{z-\alpha}{\beta-\alpha}=\displaystyle\frac{\overline{z}-\overline{\alpha}}{\overline{\beta}-\overline{\alpha}} \ }\)
\(\small{ \ \left(\overline{\beta}-\overline{\alpha}\right)\left(z-\alpha\right)=\left(\beta-\alpha\right)\left(\overline{z}-\overline{\alpha}\right) \ }\)
この\(\small{ \ \left(\overline{\beta}-\overline{\alpha}\right)\left(z-\alpha\right)=\left(\beta-\alpha\right)\left(\overline{z}-\overline{\alpha}\right) \ }\)が点\(\small{ \ \mathrm{A}(\alpha) \ }\)と点\(\small{ \ \mathrm{B}\left(\beta\right) \ }\)を通る直線を描く\(\small{ \ \mathrm{P}\left(z\right) \ }\)の満たす方程式になる。
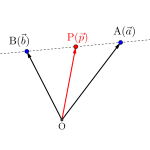
次に点\(\small{ \ \mathrm{A} \ }\)を通り、\(\small{ \ \mathrm{OB} \ }\)に垂直な直線を描く\(\small{ \ z \ }\)の満たす方程式について考えてみよう。
\(\small{ \ \mathrm{AP \perp OB} \ }\)だから
\(\small{ \ \displaystyle\frac{z-\alpha}{\beta}+\overline{\left(\displaystyle\frac{z-\alpha}{\beta}\right)}=0 \ }\)
これを整理すると
\(\small{ \ \overline{\beta}\left(z-\alpha\right)+\beta\left(\overline{z}-\overline{\alpha}\right)=0 \ }\)
この\(\small{ \ \overline{\beta}\left(z-\alpha\right)+\beta\left(\overline{z}-\overline{\alpha}\right)=0 \ }\)が点\(\small{ \ \mathrm{A} \ }\)を通り、\(\small{ \ \mathrm{OB} \ }\)に垂直な直線を描く\(\small{ \ z \ }\)の満たす方程式になる。

これらの式だけ見ても、実際に値を代入したとき、どんな形になるかわからないから次の例題を通して、どんな式の形になるのか考えてみよう。
点\(\small{ \ \mathrm{O}(0) \ }\)、点\(\small{ \ \mathrm{A}(1+i) \ }\)、点\(\small{ \ \mathrm{B}(2-i) \ }\)とする。次の問いに答えよ。
(1)点\(\small{ \ \mathrm{A} \ }\)を通り、\(\small{ \ \mathrm{OB} \ }\)に平行な直線を描く\(\small{ \ z \ }\)の満たす方程式を求めよ。
(2)点\(\small{ \ \mathrm{A} \ }\)を通り、\(\small{ \ \mathrm{OB} \ }\)に垂直な直線を描く\(\small{ \ z \ }\)の満たす方程式を求めよ。
(3)点\(\small{ \ \mathrm{A} \ }\)と点\(\small{ \ \mathrm{B} \ }\)を通る直線を描く\(\small{ \ z \ }\)の満たす方程式を求めよ。
(1)
\(\small{ \ (z-1-i)(2+i)=(2-i)\left(\overline{z}-1+i\right) \ }\)
\(\small{ \ (2+i)z-(1+i)(2+i)=(2-i)\overline{z}+(2-i)(-1+i) \ }\)
\(\small{ \ (2+i)z-(2-i)\overline{z}-6i=0 \ }\)
(2)
\(\small{ \ (z-1-i)(2+i)+(2-i)\left(\overline{z}-1+i\right)=0 \ }\)
\(\small{ \ (2+i)z-(1+i)(2+i)+(2-i)\overline{z}+(2-i)(-1+i)=0 \ }\)
\(\small{ \ (2+i)z+(2-i)\overline{z}-2=0 \ }\)
(3)
\(\small{ \ \displaystyle\frac{z-(1+i)}{1-2i}=\displaystyle\frac{\overline{z}-(1-i)}{1+2i} \ }\)
\(\small{ \ (z-1-i)(1+2i)=\left(\overline{z}-(1-i)\right)(1-2i) \ }\)
\(\small{ \ (1+2i)z-(1-2i)\overline{z}-6i=0 \ }\)

-

直線のベクトル方程式
二点を通る直線や法線ベクトルを利用した直線などを詳しく解説しています。
続きを見る
方程式から図形を求める
最後に与えられた方程式から図形を求める方法について考えてみよう。
上の例題の(1)の答えの式\(\small{ \ (2+i)z-(2-i)\overline{z}-6i=0 \ }\)から\(\small{ \ \displaystyle\frac{z-(1+i)}{2-i}=\displaystyle\frac{\overline{z}-(1-i)}{2+i} \ }\)を導いて、「\(\small{ \ z \ }\)は点\(\small{ \ \mathrm{A} \ }\)を通り、\(\small{ \ \mathrm{OB} \ }\)に平行な直線を描く」ってできればいいけど、\(\small{ \ (2+i)z-(2-i)\overline{z}-6i=0 \ }\)から\(\small{ \ \displaystyle\frac{z-(1+i)}{2-i}=\displaystyle\frac{\overline{z}-(1-i)}{2+i} \ }\)に式変形するのって、まず無理だよね。複素数の展開は簡単だけど因数分解は難しいよね。
だからこの方程式から\(\small{ \ z \ }\)を求める場合は\(\small{ \ z=x+yi \ }\)として式を整理して求めよう。
\(\small{ \ (2+i)z-(2-i)\overline{z}-6i=0 \ }\)
\(\small{ \ (2x+4y-6)i=0 \ }\)
\(\small{ \ \therefore x+2y-3=0 \ }\)
これで\(\small{ \ 3 \ }\)と\(\small{ \ \displaystyle\frac{3}{2}i \ }\)を通る直線ってわかる。直線は二点が決まればいいから\(\small{ \ 3 \ }\)と\(\small{ \ \displaystyle\frac{3}{2}i \ }\)じゃなくてもいいんだけど、実軸、虚軸との交点が調べやすいよね。元の問題みたいに点\(\small{ \ \mathrm{A} \ }\)を通り、\(\small{ \ \mathrm{OB} \ }\)に平行な直線って言えなくはないけど、二点を指定したほうが簡単だよね。
次の方程式を満たす点\(\small{ \ z \ }\)全体は、どのような図形を描くか。
(1)\(\small{ \ (2+i)z+(2-i)\overline{z}-2=0 \ }\)
(2)\(\small{ \ (1+2i)z-(1-2i)\overline{z}-6i=0 \ }\)
(1)\(\small{ \ (2+i)z+(2-i)\overline{z}-2=0 \ }\)
\(\small{ \ z=x+yi \ }\)とすると
\(\small{ \ 4x-2y-2=0 \ }\)
\(\small{ \ \therefore \ 2x-y-1=0 \ }\)
\(\small{ \ i \ }\)と\(\small{ \ \displaystyle\frac{1}{2} \ }\)を通る直線
(2)\(\small{ \ (1+2i)z-(1-2i)\overline{z}-6i=0 \ }\)
\(\small{ \ z=x+yi \ }\)とすると
\(\small{ \ (4x+2y-6)i=0 \ }\)
\(\small{ \ \therefore 2x+y-3=0 \ }\)
\(\small{ \ 3i \ }\)と\(\small{ \ \displaystyle\frac{3}{2} \ }\)を通る直線

①\(\small{ \ z \ }\)のまま解く
②\(\small{ \ z=a+bi \ }\)として解く
③極形式\(\small{ \ z=r(\cos \theta+i\sin \theta) \ }\)で解く
④座標を利用して解く
⑤図形の性質を利用して解く
がある。
\(\small{ \ z \ }\)のまま式を展開する(①の利用)のはできるけど、それを元に戻すのは難しいからそのときは\(\small{ \ z=x+yi \ }\)を利用しよう(②の利用)。
Point 複素数と図形(直線の応用)
①平行条件\(\small{ \ \displaystyle\frac{\sigma-\gamma}{\beta-\alpha}=\overline{\left(\displaystyle\frac{\sigma-\gamma}{\beta-\alpha}\right)} \ }\)を覚える
②垂直条件\(\small{ \ \displaystyle\frac{\sigma-\gamma}{\beta-\alpha}+\overline{\left(\displaystyle\frac{\sigma-\gamma}{\beta-\alpha}\right)}=0 \ }\)を覚える
③\(\small{ \ z \ }\)と\(\small{ \ x+yi \ }\)の利用方法をマスターする