こんにちは、リンス(@Lins016)です。
今回は複素数と図形(円)について学習していこう。
複素数平面上の図形
複素数平面上の図形の第2回目は円について学習していこう。前回は複素数平面上の直線だったから、直線をまだ確認していない人は複素数と図形(直線)を確認してから進めていこう。
-

複素数と図形(直線)
複素数平面に描かれる直線の方程式について詳しく解説しています。
続きを見る
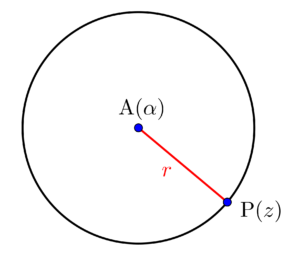
点\(\small{ \ \mathrm{A}\left(\alpha\right) \ }\)を中心とする半径\(\small{ \ r \ }\)の円
\(\small{ \ |z-\alpha|=r \ }\)
円を表す図形の方程式
円は「円の中心と半径」が大切だよね。これさえ分かっていれば円を書くことができるからね。これは図形と方程式やベクトル方程式のときも同じだよね。
円は中心からの距離が等しい点の集まりだから、点\(\small{ \ \mathrm{P}\left(z\right) \ }\)は中心が点\(\small{ \ \mathrm{A}\left(\alpha\right) \ }\)、半径\(\small{ \ r \ }\)の円を描くとき次の方程式を満たす。
\(\small{ \ |z-\alpha|=r \ }\)
これが複素数平面で円を表す方程式の形になるから覚えておこう。
絶対値記号を外した円の方程式
\(\small{ \ |z-\alpha|=r \ }\)が円の方程式になるのは分かったけど、試験ではこの形に自分で導かないといけない。
そもそも半径と中心が先にわかってることってほとんどないよね。だからこの\(\small{ \ |z-\alpha|=r \ }\)の形は最終形になるんだ。図形と方程式でいうところの\(\small{ \ (x-a)^2+(y-b)^2=r^2 \ }\)のこと。
式を見ただけで中心と半径がわかる形だよね。
でも図形と方程式の座標平面でも\(\small{ \ x^2+y^2+lx+my+n=0 \ }\)の形みたいに円ってわかるけど、中心と半径は式変形しないとわからないことってあるよね。
これと同じように複素数平面でも\(\small{ \ |z-\alpha|=r \ }\)の前にもう一つ式があるんだ。それは絶対値記号を外した形になる。
それじゃ\(\small{ \ |z-\alpha|=r \ }\)の絶対値記号を外してみよう。
\(\small{ \ |z|^2=z\overline{z} \ }\)になることに注意して、両辺\(\small{ \ 2 \ }\)乗すると
\(\small{ \ |z-\alpha|^2=r^2 \ }\)
\(\small{ \ \left(z-\alpha\right)\overline{\left(z-\alpha\right)}=r^2 \ }\)
\(\small{ \ \left(z-\alpha\right)\left(\overline{z}-\overline{\alpha}\right)=r^2 \ }\)
\(\small{ \ z\overline{z}-\overline{\alpha}z-\alpha\overline{z}-\alpha\overline{\alpha}-r^2=0 \ }\)
この形が絶対値記号を外した円の方程式になる。このとき\(\small{ \ \alpha \ }\)は中心を表す複素数だから\(\small{ \ \alpha=1+2i \ }\)のように\(\small{ \ a+bi \ }\)の形をしてる。
だから\(\small{ \ \alpha\overline{\alpha}=|\alpha|^2 \ }\)は、\(\small{ \ \alpha=a+bi \ }\)なら\(\small{ \ |\alpha|^2=a^2+b^2 \ }\)になって\(\small{ \ -\alpha\overline{\alpha}-r^2 \ }\)は実数になって計算できるからね。
\(\small{ \ |z-1-i|=2 \ }\)の絶対値記号を外した方程式を求めよ。
\(\small{ \ |z-1-i|=2 \ }\)
\(\small{ \ |z-1-i|^2=4 \ }\)
\(\small{ \ (z-1-i)\overline{(z-1-i)}=4 \ }\)
\(\small{ \ (z-1-i)(\overline{z}-1+i)=4 \ }\)
\(\small{ \ z\overline{z}+(-1+i)z-(1+i)\overline{z}-2=0 \ }\)
アポロニウスの円と複素数平面
アポロニウスの円とは\(\small{ \ 2 \ }\)点\(\small{ \ \mathrm{A} \ }\)、\(\small{ \ \mathrm{B} \ }\)と点\(\small{ \ \mathrm{P} \ }\)の距離の比\(\small{ \ \mathrm{AP:BP} \ }\)が一定(\(\small{ \ \mathrm{AP\neq BP} \ }\))のときの点\(\small{ \ \mathrm{P} \ }\)の軌跡のことで、これは円を描く。
図形と方程式の軌跡でもよく出題されるけど、これを複素数平面で考えてみよう。
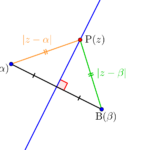
\(\small{ \ \mathrm{A}(\alpha) \ }\)、\(\small{ \ \mathrm{B}(\beta) \ }\)と\(\small{ \ \mathrm{P}(z) \ }\)のとき、\(\small{ \ \mathrm{AP:BP}=m:n \ }\)とすると
\(\small{ \ |z-\alpha|:|z-\beta|=m:n \ }\)
\(\small{ \ n|z-\alpha|=m|z-\beta| \ }\)
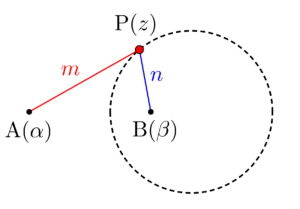
これを具体的な数値で考えてみよう。
\(\small{ \ 1 \ }\)、\(\small{ \ i \ }\)からの距離が\(\small{ \ 3:2 \ }\)になる点\(\small{ \ z \ }\)の表す図形を考えてみよう。
\(\small{ \ |z-1|:|z-i|=3:2 \ }\)
\(\small{ \ 3|z-i|=2|z-1| \ }\)
\(\small{ \ 9|z-i|^2=4|z-1|^2 \ }\)
\(\small{ \ 9z\overline{z}+9iz-9i\overline{z}+9=4z\overline{z}-4z-4\overline{z}+4 \ }\)
\(\small{ \ 5z\overline{z}+(4+9i)z+(4-9i)\overline{z}+5=0 \ }\)
\(\small{ \ z\overline{z}+\displaystyle\frac{4+9i}{5}z+\displaystyle\frac{4-9i}{5}\overline{z}+1=0 \ }\)
\(\small{ \ z\overline{z}+\left(\overline{\displaystyle\frac{4+9i}{5}}\right)z+\displaystyle\frac{4-9i}{5}\overline{z}+1=0 \ }\)
\(\small{ \ \left(z+\displaystyle\frac{4-9i}{5}\right)\left(\overline{z+\displaystyle\frac{4-9i}{5}}\right)-\left(\displaystyle\frac{4+9i}{5}\right)\left(\overline{\displaystyle\frac{4+9i}{5}}\right)+1=0 \ }\)
\(\small{ \ \left|z+\displaystyle\frac{4-9i}{5}\right|^2=\displaystyle\frac{72}{25} \ }\)
\(\small{ \ \left|z+\displaystyle\frac{4-9i}{5}\right|=\displaystyle\frac{6\sqrt{2}}{5} \ }\)
これで点\(\small{ \ -\displaystyle\frac{4}{5}+\displaystyle\frac{9}{5}i \ }\)を中心とする半径\(\small{ \ \displaystyle\frac{6\sqrt{2}}{5} \ }\)の円を描くことがわかる。
この計算は\(\small{ \ n|z-\alpha|=m|z-\beta| \ }\)から絶対値記号を外して、式を整理して、また絶対値記号を含めた円の形に変形する。大変な計算だけど、確実にできるようにしておかないといけないからね。
次の方程式を満たす点\(\small{ \ z \ }\)全体は、どのような図形を描くか。
(1)\(\small{ \ |z+1|=2|z-2| \ }\)
(2)\(\small{ \ |\overline{z}-1-i|=2 \ }\)
(1)\(\small{ \ |z+1|=2|z-2| \ }\)
\(\small{ \ |z+1|^2=4|z-2|^2 \ }\)
\(\small{ \ 3z\overline{z}-9z-9\overline{z}+15 \ }\)
\(\small{ \ z\overline{z}-3z-3\overline{z}+5 \ }\)
\(\small{ \ \left(z-3\right)\left(\overline{z}-3\right)-4=0 \ }\)
\(\small{ \ |z-3|^2=4 \ }\)
\(\small{ \ |z-3|=2 \ }\)
点\(\small{ \ 3 \ }\)を中心とする半径\(\small{ \ 2 \ }\)の円
(2)\(\small{ \ |\overline{z}-1-i|=2 \ }\)
\(\small{ \ |\overline{z-1+i}|=2 \ }\)
\(\small{ \ |z-1+i|=2 \ }\)
点\(\small{ \ 1-i \ }\)を中心とする半径\(\small{ \ 2 \ }\)の円

Point 複素数と図形(円)
①\(\small{ \ |\overline{z-\alpha}|=r \ }\)から中心と半径を求める
②絶対値記号がない\(\small{ \ z\overline{z}-\overline{\alpha}z-\alpha\overline{z}-\alpha\overline{\alpha}-r^2=0 \ }\)を
\(\small{ \ |\overline{z-\alpha}|=r \ }\)に変形できるようにする
③\(\small{ \ n|z-\alpha|=m|z-\beta| \ }\)はアポロニウスの円
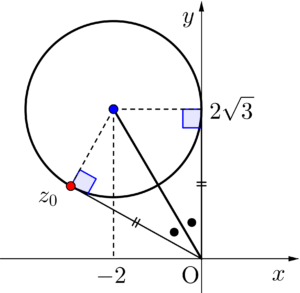
(1)等式\(\small{ \ z\overline{z}+2\left(z+\overline{z}\right)+2\sqrt{3}i\left(z-\overline{z}\right)+12=0 \ }\)を満たす\(\small{ \ z \ }\)全体を求め、その図形を複素数平面上に図示せよ。
(2)\(\small{ \ a \ }\)の値を正の実数とする。複素数\(\small{ \ z_0 \ }\)は\(\small{ \ z_0 ^3=ia \ }\)を満たし、かつ\(\small{ \ z_0 \ }\)は(1)で求めた図形上にあるとする。このとき、\(\small{ \ a \ }\)と\(\small{ \ z_0 \ }\)の値をそれぞれ求めよ。
(1)
\(\small{ \ \left(z+2-2\sqrt{3}i\right)\left(\overline{z}+2+2\sqrt{3}i\right)=4 \ }\)
\(\small{ \ \left(z+2-2\sqrt{3}i\right)\left(\overline{z+2-2\sqrt{3}i}\right)=4 \ }\)
\(\small{ \ \left|z+2-2\sqrt{3}i\right|^2=4 \ }\)
\(\small{ \ \left|z+2-2\sqrt{3}i\right|=2 \ }\)
よって点\(\small{ \ -2+2\sqrt{3}i \ }\)を中心とする半径\(\small{ \ 2 \ }\)の円

(2)
\(\small{ \ z_0=r\left(\cos\theta+i\sin\theta\right) \ }\)
\(\small{ \ \left(r\gt0, \ 0\leqq \theta\lt2\pi\right) \ }\)とおく
(1)より\(\small{ \ z_0 \ }\)が点\(\small{ \ -2+2\sqrt{3}i \ }\)を中心とする半径\(\small{ \ 2 \ }\)の円周上を動くとき
\(\small{ \ \displaystyle\frac{\pi}{2}\leqq \theta \leqq \displaystyle\frac{5}{6}\pi \ }\)
\(\small{ \ z_0 ^3=r^3\left(\cos3\theta+i\sin3\theta\right) \ }\)
\(\small{ \ z_0 ^3=ia=a\left(\cos\displaystyle\frac{\pi}{2}+i\sin\displaystyle\frac{\pi}{2}\right) \ }\)より
\(\small{ \ r^3=a, \ 3\theta=\displaystyle\frac{\pi}{2}+2n\pi \ }\)(\(\small{ \ n \ }\)は整数)
\(\small{ \ \theta=\displaystyle\frac{\pi}{6}+\displaystyle\frac{2}{3}n\pi \ }\)
\(\small{ \ \displaystyle\frac{\pi}{2}\leqq \theta \leqq \displaystyle\frac{5}{6}\pi \ }\)より\(\small{ \ \theta=\displaystyle\frac{5}{6}\pi \ }\)
このとき図より\(\small{ \ r=2\sqrt{3} \ }\)
よって
\(\small{\begin{eqnarray} \ z_0&=&2\sqrt{3}\left(\cos\displaystyle\frac{5}{6}\pi+i\sin\displaystyle\frac{5}{6}\pi\right)\\[3pt]
&=&-3+\sqrt{3}i \ \end{eqnarray}}\)
また\(\small{ \ a=r^3 \ }\)より\(\small{ \ a=24\sqrt{3} \ }\)