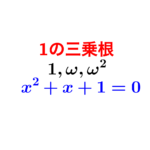複素数のn乗根

こんにちは、リンス(@Lins016)です。
今回は複素数の\(\small{ \ n \ }\)乗根について学習していこう。

複素数のn乗根とその求め方

複素数\(\small{ \ \alpha \ }\)と正の整数\(\small{ \ n \ }\)に対して、\(\small{ \ z^n=\alpha \ }\)の解を\(\small{ \ \alpha \ }\)の\(\small{ \ n \ }\)乗根っていうんだ。

\(\small{ \ n \ }\)乗すると\(\small{ \ \alpha \ }\)になるもののことね。

ちなみに\(\small{ \ 0 \ }\)じゃない複素数の\(\small{ \ n \ }\)乗根は\(\small{ \ n \ }\)個あるから覚えておこう。

1のn乗根

\(\small{ \ z^n=1 \ }\)の解、\(\small{ \ 1 \ }\)の\(\small{ \ n \ }\)乗根を求めるんだけど、まずは\(\small{ \ z^3=1 \ }\)の解\(\small{ \ 1 \ }\)の\(\small{ \ 3 \ }\)乗根を求めてみよう。

まずは今まで勉強した因数分解で求めてみよう。
\(\small{ \ z^3=1\\[3pt] (z-1)(z^2+z+1)=0\\[3pt] z=1, \ \displaystyle\frac{-1\pm \sqrt{3}i}{2} \ }\)
\(\small{ \ 1 \ }\)の三乗根ってかなり有名な値だったよね。忘れている人は一度確認しておこう。

因数分解して求めることができる三乗根や四乗根ぐらいならいいけど、それ以上になると因数分解で解を求めるのは難しくなるよね。

その場合は極形式を利用して解くんだ。
このまま進める前に極形式について不安がある人は一度確認しておこう。

\(\small{ \ z^3=1 \ }\)の左辺の\(\small{ \ z \ }\)を\(\small{ \ z=r \left(\cos \theta+i \sin \theta\right) \ }\)とおくと\(\small{ \ z^3=r^3 \left(\cos 3\theta+i \sin 3\theta\right) \ }\)になるよね。

これに対して右辺の\(\small{ \ 1 \ }\)を極形式にすると、\(\small{ \ 1=\cos 0+i \sin 0 \ }\)になるよね。

一般角を使うと\(\small{ \ 1=\cos \left(0+2n\pi\right)+i \sin \left(0+2n\pi\right) \ }\)になるから\(\small{ \ r^3 \left(\cos 3\theta+i \sin 3\theta\right) \ }\)と絶対値と偏角を比較して
\(\small{ \begin{eqnarray}
\left\{
\begin{array}{l}
r^3=1 \\
3\theta=0+2k\pi(k)
\end{array}
\right.
\end{eqnarray} \ }\)

絶対値\(\small{ \ r\gt0 \ }\)より\(\small{ \ r=1 \ }\)、偏角は\(\small{ \ \theta=0+\displaystyle\frac{2k\pi}{3} \ }\)になる。

このとき\(\small{ \ 0\leqq \theta \lt 2\pi \ }\)を満たすのは\(\small{ \ k=0, \ 1, \ 2 \ }\)になる。

これって\(\small{ \ z^n=\alpha \ }\)の解が\(\small{ \ n \ }\)個あることを覚えておけば、\(\small{ \ k=0, \ 1 \ ,\cdots,n-1 \ }\) の\(\small{ \ n \ }\)個になるんだ。

\(\small{ \ z^n=r^n\left(\cos n\theta+i\sin n\theta\right) \ }\)
\(\small{ \ \alpha=r'\left(\cos \theta'+i\sin \theta'\right) \ }\)
とすると
\(\small{ \ n\theta=\theta'+2k\pi \ }\)で\(\small{ \ \theta=\displaystyle\frac{\theta'}{n}+\displaystyle\frac{2k}{n}\pi \ }\)になって、\(\small{ \ 0\leqq \theta \lt 2\pi \ }\)の範囲になる\(\small{ \ k \ }\)の値を考えればいいんだけど、\(\small{ \ z^n=\alpha \ }\)の解が\(\small{ \ n \ }\)個あるから\(\small{ \ k=0, \ 1,\cdots,n-1 \ }\) の\(\small{ \ n \ }\)個って覚えてたほうが楽だよね。

話を\(\small{ \ z^3=1 \ }\)に戻して、偏角は\(\small{ \ \theta=0+\displaystyle\frac{2k\pi}{3} \ }\)の\(\small{ \ k=0, \ 1, \ 2 \ }\)になる。

\(\small{ \ z_k=\cos \displaystyle\frac{2k\pi}{3}+i \sin \displaystyle\frac{2k\pi}{3} \ \left(k=0, \ 1, \ 2\right) \ }\)
\(\small{ \ z_0=1 \ }\)
\(\small{ \ z_1=\cos \displaystyle\frac{2}{3}\pi+i\sin \displaystyle\frac{2}{3}\pi=-\displaystyle\frac{1}{2}+\displaystyle\frac{\sqrt{3}}{2}i \ }\)
\(\small{ \ z_2=\cos \displaystyle\frac{4}{3}\pi+i\sin \displaystyle\frac{4}{3}\pi=-\displaystyle\frac{1}{2}-\displaystyle\frac{\sqrt{3}}{2}i \ }\)

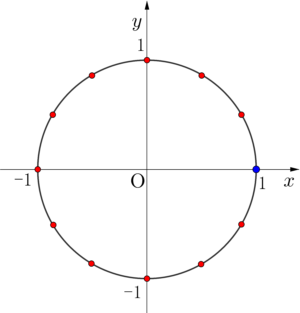
これって単位円の円周上にあり、円周を三等分する点になるのもわかるよね。

一般に\(\small{ \ z^n=1 \ }\)の解である\(\small{ \ 1 \ }\)の\(\small{ \ n \ }\)乗根は次の\(\small{ \ n \ }\)個の複素数になる。

\(\small{ \ z_k=\cos \displaystyle\frac{2k\pi}{n}+i \sin \displaystyle\frac{2k\pi}{n} \ (k=0, \ 1,\cdots,n-1) \ }\)

ちなみに複素数平面上で\(\small{ \ z^n=1 \ }\)の解の\(\small{ \ 1 \ }\)の\(\small{ \ n \ }\)乗根を表す点は単位円に内接する正\(\small{ \ n \ }\)角形の頂点になって、そのうち頂点の一つは\(\small{ \ 1 \ }\)になるんだ。

問題解答

\(\small{ \ z^4=-8+8\sqrt{3}i \ }\)を満たす\(\small{ \ z \ }\)の値を求めよ。

\(\small{ \ z=r\left(\cos\theta+i\sin\theta\right) \ }\)ただし、\(\small{ \ r\gt0 \ }\)とおく
\(\small{ \ z^4=r^4\left(\cos4\theta+i\sin4\theta\right)\cdots① \ }\)

\(\small{ \ -8+8\sqrt{3}i\\[3pt] \ =16(-\displaystyle\frac{1}{2}+\displaystyle\frac{\sqrt{3}}{2}i)\\[3pt] \ =16\left\{\cos\left(\displaystyle\frac{2}{3}\pi+2k\pi\right)+i\sin\left(\displaystyle\frac{2}{3}\pi+2k\pi\right)\right\}\cdots② \ }\)

\(\small{ \ ①,② \ }\)の絶対値と偏角を比較して
\(\small{ \ \begin{eqnarray}
\left\{
\begin{array}{l}
r^4=16\\
4\theta=\displaystyle\frac{2}{3}\pi+2k\pi
\end{array}
\right.
\end{eqnarray} \ }\)

よって
\(\small{ \ r=2, \ \theta=\displaystyle\frac{1}{6}\pi+\displaystyle\frac{k}{2}\pi \ }\)
\(\small{ \ 0\leqq \theta \lt 2\pi \ }\)より\(\small{ \ k=0, \ 1, \ 2, \ 3 \ }\)

よって求める\(\small{ \ z \ }\)は
\(\small{ \ \begin{eqnarray}
z
&=&
\begin{cases}
2\left(\cos\displaystyle\frac{1}{6}\pi+i\sin\displaystyle\frac{1}{6}\pi\right)\\[3pt] 2\left(\cos\displaystyle\frac{2}{3}\pi+i\sin\displaystyle\frac{2}{3}\pi\right)\\[3pt] 2\left(\cos\displaystyle\frac{7}{6}\pi+i\sin\displaystyle\frac{7}{6}\pi\right)\\[3pt] 2\left(\cos\displaystyle\frac{5}{3}\pi+i\sin\displaystyle\frac{5}{3}\pi\right)
\end{cases}\\[3pt] &=&
\begin{cases}
\sqrt{3}+i\\[3pt] -1+\sqrt{3}i\\[3pt] -\sqrt{3}-i\\[3pt] 1-\sqrt{3}i\end{cases}
\end{eqnarray}
\ }\)

Point 複素数の\(\small{ \ n \ }\)乗根

①\(\small{ \ z=r(\cos \theta+i \sin \theta) \ }\)からド・モアブルの定理を利用する
②\(\small{ \ \alpha \ }\)の\(\small{ \ n \ }\)乗根は\(\small{ \ n \ }\)個ある