複素数平面とその基本

こんにちは、リンス(@Lins016)です。
今回は複素数平面とその基本について学習していこう。

複素数平面

複素数は\(\small{ \ a+bi \ }\)(\(\small{ \ a, \ b \ }\)は実数)の形に表されるものだったよね。これは数学IIで学習した通りだからね。

数学Ⅲではこれを平面座標に表記して、図形として考えたりしていくんだ。
この平面のことを複素数平面っていうんだ。（古い参考書とかだと複素平面やガウス平面とも書いてあるかな。）

まず複素数平面を学習する上で基本となる考え方について話をしていきたいと思う。

そして少し長いけど記事をきちんと読んで例題と入試問題にチャレンジを自分で解いてみよう。

複素数平面

複素数平面では複素数\(\small{ \ z=a+bi \ }\)を平面座標上の点\(\small{ \ (a, \ b) \ }\)に対応させる。

これは\(\small{ \ x \ }\)軸を実軸、\(\small{ \ y \ }\)軸を虚軸とした平面になるから、実部\(\small{ \ a \ }\)と虚部\(\small{ \ b \ }\)を座標上の点として対応するんだ。

ただ注意してないといけないのが、今まで学習してきた\(\small{ \ xy \ }\)平面上の点\(\small{ \ \mathrm{P} \ }\)は\(\small{ \ (a, \ b) \ }\)って表してきたけど、複素数\(\small{ \ z \ }\)を表す点\(\small{ \ \mathrm{P} \ }\)は複素数平面上では\(\small{ \ (a, \ b) \ }\)と書かずに\(\small{ \ \mathrm{P}(z) \ }\)って書くから覚えておこう。

複素数\(\small{ \ z \ }\)が\(\small{ \ \displaystyle\frac{p+qi}{s+ti} \ }\)の形のときは分母分子に\(\small{ \ s-ti \ }\)をかけて有理化して\(\small{ \ a+bi \ }\)の形に変えて複素平面上に書き込もう。

特に実軸上にある複素数は実数になるし、虚軸上にある複素数は虚数になるから注意しよう。

共役複素数

\(\small{ \ z=a+bi \ }\)に対して虚部の符号が変わる\(\small{ \ a-bi \ }\)の複素数を\(\small{ \ z \ }\)の共役複素数と言って、\(\small{ \ \bar{z} \ }\)と表すんだ。

複素数平面で\(\small{ \ z \ }\)と\(\small{ \ \bar{z} \ }\)は\(\small{ \ x \ }\)軸（実軸）に対して対称になるからね。

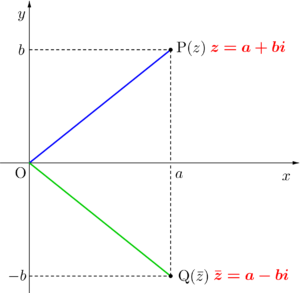
ちなみに\(\small{ \ a-bi \ }\)の共役複素数は\(\small{ \ a+bi \ }\)になるから\(\small{ \ \overline{\bar{z}}=z \ }\)になるからね。

複素数の絶対値

原点\(\small{ \ \mathrm{O} \ }\)と点\(\small{ \ \mathrm{P}(z) \ }\)との距離を\(\small{ \ z \ }\)の絶対値って言って\(\small{ \ |z| \ }\)で表すんだ。

複素数\(\small{ \ z=a+bi \ }\)の絶対値は原点\(\small{ \ \mathrm{O} \ }\)と点\(\small{ \ \mathrm{P}(z) \ }\)の距離だから\(\small{ \ \mathrm{OP}=\sqrt{a^2+b^2} \ }\)になる。

だから\(\small{ \ z=a+bi \ }\)のとき\(\small{ \ |z|=\sqrt{a^2+b^2} \ }\)になるんだ。

ここで\(\small{ \ z=a+bi \ }\)のとき\(\small{ \ \bar{z}=a-bi \ }\)だから\(\small{ \ z\bar{z}=(a+bi)(a-bi)=a^2+b^2 \ }\)になる。
これって\(\small{ \ |z|^2 \ }\)だよね。

つまり\(\small{ \ |z|^2=z\bar{z} \ }\)になるんだ。この式ってかなり重要な式だから確実に覚えておこう。

複素数の計算と図形

・複素数の和と差
複素数\(\small{ \ \alpha=a+bi \ }\)と\(\small{ \ \beta=c+di \ }\)の計算（和・差）って数学IIで教わったと思うけど、
\(\small{ \ \alpha+\beta=(a+c)+(b+d)i \ }\)
\(\small{ \ \alpha-\beta=(a-c)+(b-d)i \ }\)
つまり実部同士、虚部同士を計算すればよかったよね。

これを図形的に考えてみよう。

点\(\small{ \ \mathrm{A}(\alpha) \ }\)と点\(\small{ \ \mathrm{B}(\beta) \ }\)に対して点\(\small{ \ \mathrm{C}(\alpha+\beta) \ }\)と点\(\small{ \ \mathrm{D}(\alpha-\beta) \ }\)は図の位置になる。

これってベクトルの考え方に似てるよね。平行四辺形を作って図示できるんだ。

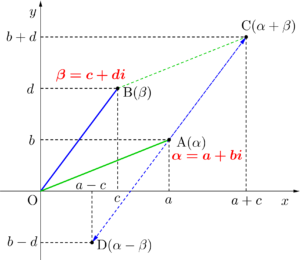
原点\(\small{ \ \mathrm{O} \ }\)と点\(\small{ \ \mathrm{C} \ }\)の距離が\(\small{ \ \alpha+\beta \ }\)の絶対値になるから
\(\small{ \ |\alpha+\beta|=\sqrt{(a+c)^2+(b+d)^2} \ }\)になる。

また、点\(\small{ \ \mathrm{A}(\alpha) \ }\)と点\(\small{ \ \mathrm{B}(\beta) \ }\)の距離は、原点\(\small{ \ \mathrm{O} \ }\)と点\(\small{ \ \mathrm{D}(\alpha-\beta) \ }\)の距離と等しいから
\(\small{ \ |\alpha-\beta|=\sqrt{(a-c)^2+(b-d)^2} \ }\)になる。

・同一直線上の複素数

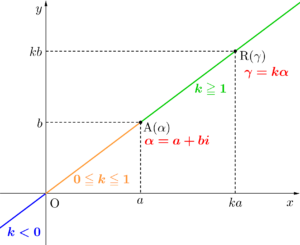
さらに複素数\(\small{ \ \alpha \ }\)を実数倍した\(\small{ \ \gamma=k\alpha \ }\)について考えてみよう。

これは、原点\(\small{ \ \mathrm{O} \ }\)と点\(\small{ \ \mathrm{A}(\alpha) \ }\)を結ぶ直線上にあることが言えるからね。

点\(\small{ \ \mathrm{R}(\gamma) \ }\)は\(\small{ \ 0\leqq k \leqq 1 \ }\)なら線分\(\small{ \ \mathrm{OA} \ }\)上の位置にあるし、\(\small{ \ k\lt0 \ }\)なら原点に関して点\(\small{ \ \mathrm{A} \ }\)と反対側、\(\small{ \ k\gt1 \ }\)なら点\(\small{ \ \mathrm{A} \ }\)に関して原点と反対側の位置にあるんだ。

原点\(\small{ \ \mathrm{O}(0) \ }\)と点\(\small{ \ \mathrm{A}(\alpha) \ }\)と点\(\small{ \ \mathrm{B}(\beta) \ }\)が同一直線上にあるとき\(\small{ \ \beta=k\alpha \ }\)（\(\small{ \ k \ }\)は実数）が成り立つってことだからね。

共役複素数の性質

\(\small{ \ \alpha=a+bi, \ \beta=c+di \ }\)とすると\(\small{ \ \bar{\alpha}=a-bi, \ \bar{\beta}=c-di \ }\)になる。
この共役複素数の性質について見ていこう。
\(\small{ \ \alpha+\beta=(a+c)+(b+d)i \ }\)だから\(\small{ \ \overline{\alpha+\beta}=(a+c)-(b+d)i \ }\)になる。
\(\small{ \ \bar{\alpha}=a-bi, \ \bar{\beta}=c-di \ }\)から
\(\small{ \ \bar{\alpha}+\bar{\beta}=(a+c)-(b+d)i \ }\)
つまり\(\small{ \ \overline{\alpha+\beta}=\bar{\alpha}+\bar{\beta} \ }\)が言えるよね。

同様に
\(\small{ \ \alpha-\beta=(a-c)+(b-d)i \ }\)だから\(\small{ \ \overline{\alpha-\beta}=(a-c)-(b-d)i \ }\)になる。
\(\small{ \ \bar{\alpha}=a-bi, \ \bar{\beta}=c-di \ }\)から\(\small{ \ \bar{\alpha}-\bar{\beta}=(a-c)+(-b+d)i \ }\)
つまり\(\small{ \ \overline{\alpha-\beta}=\bar{\alpha}-\bar{\beta} \ }\)も言える。

さらに
\(\small{ \ \alpha\beta=(ac-bd)+(ad+bc)i \ }\)だから\(\small{ \ \overline{\alpha\beta}=(ac-bd)-(ad+bc)i \ }\)になる。
ここで
\(\small{\begin{eqnarray} \ \bar{\alpha}\bar{\beta}&=&(a-bi)(c-di)\\[3pt]&=&(ac-bd)-(ad+bd)i \ \end{eqnarray}}\)
になるから\(\small{ \ \overline{\alpha\beta}=\bar{\alpha}\bar{\beta} \ }\)が言えるよね。

\(\small{ \ \displaystyle\frac{\alpha}{\beta}=\displaystyle\frac{a+bi}{c+di}=\displaystyle\frac{ac+bd+(bc-ad)i}{c^2+d^2} \ }\)だから\(\small{ \ \overline{\left(\displaystyle\frac{\alpha}{\beta}\right)}=\displaystyle\frac{ac+bd-(bc-ad)i}{c^2+d^2} \ }\)になる。
ここで\(\small{ \ \displaystyle\frac{\bar{\alpha}}{\bar{\beta}}=\displaystyle\frac{(a-bi)}{(c-di)}=\displaystyle\frac{ac+bd+(ad-bc)i}{c^2+d^2} \ }\)になるから
\(\small{ \ \overline{\left(\displaystyle\frac{\alpha}{\beta}\right)}=\displaystyle\frac{\bar{\alpha}}{\bar{\beta}} \ }\)が言える。

こんな証明が必要かというとそんなことはないけど、絶対覚えておいて欲しい性質だから、結果だけは確実に押さえておこう。

また、特に有名な性質として、
\(\small{ \ \alpha+\bar{\alpha}=a+bi+a-bi=2a \ }\)から
\(\small{ \ \alpha+\bar{\alpha} \ }\)は実数

\(\small{ \ \alpha-\bar{\alpha}=a+bi-(a-bi)=2bi \ }\)から
\(\small{ \ \alpha+\bar{\alpha} \ }\)は純虚数っていうのもある。

これも絶対覚えておいて欲しい性質になるからね。

複素数平面の考え方（計算・図形）

複素数の計算だけならゴリゴリ計算を進めればいいんだけど、それをわざわざ複素数平面にするってことは図形的性質を利用したいっていう側面もあるんだ。

さらにこの後学習する極形式っていう\(\small{ \ z=r(\cos \theta+i \sin \theta) \ }\)っていう表示形式もある。

だから数学Ⅲの複素数平面では一つの問題でも様々な解き方があるんだ。

次の例題を複数の解き方をしてどんな解き方があるか考えてみよう。

問題解答1解答2解答3解答4

\(\small{ \ 3z+\bar{z}=3-4i \ }\)を満たすとき、\(\small{ \ z \ }\)を求めよ。

両辺の共役を考えると
\(\small{ \ 3\bar{z}+z=3+4i \ }\)
連立して
\(\small{ \begin{eqnarray}
\left\{
\begin{array}{l}
3z+\bar{z}=3-4i\cdots①\\
z+3\bar{z}=3+4i\cdots②
\end{array}
\right.
\end{eqnarray} \ }\)
\(\small{ \ ①\times3-② \ }\)より
\(\small{ \ 8z=6-16i \ }\)
\(\small{ \ \therefore z=\displaystyle\frac{3}{4}-2i \ }\)

\(\small{ \ z=a+bi \ }\)（ \(\small{ \ a, \ b \ }\)は実数）とする。
\(\small{ \ \bar{z}=a-bi \ }\)より
\(\small{ \ 3(a+bi)+(a-bi)=3-4i \ }\)
\(\small{ \ 4a+2bi=3-4i \ }\)
両辺の実部と虚部を比較して
\(\small{ \ 4a=3 \ }\)\(\small{ \ a=\displaystyle\frac{3}{4} \ }\)
\(\small{ \ 2b=-4 \ }\)\(\small{ \ b=-2 \ }\)
\(\small{ \ \therefore z=\displaystyle\frac{3}{4}-2i \ }\)

\(\small{ \ 3z+\bar{z} \ }\)を\(\small{ \ 3z \ }\)と\(\small{ \ \bar{z} \ }\)にわけて複素数平面上で考えると図のようになる。
図より\(\small{ \ 3z+\bar{z} \ }\)の実部は\(\small{ \ z \ }\)の実部の\(\small{ \ 4 \ }\)倍
\(\small{ \ 3z+\bar{z} \ }\)の虚部は\(\small{ \ z \ }\)の虚部の\(\small{ \ 2 \ }\)倍

よって\(\small{ \ z=\displaystyle\frac{3}{4}-2i \ }\)

\(\small{ \ 3z+\bar{z}=3-4i \ }\)
この式を変形して
\(\small{ \ 2z+(z+\bar{z})=3-4i \ }\)
ここで\(\small{ \ z+\bar{z} \ }\)は実数になるから\(\small{ \ 2z \ }\)の虚部が\(\small{ \ -4 \ }\)である
よって\(\small{ \ z \ }\)の虚部は\(\small{ \ -2 \ }\)である
さらに式を次のように変形する
\(\small{ \ 4z-(z-\bar{z})=3-4i \ }\)
ここで\(\small{ \ z-\bar{z} \ }\)は純虚数になるから\(\small{ \ 4z \ }\)の実部が\(\small{ \ 3 \ }\)である
よって\(\small{ \ z \ }\)の実部は\(\small{ \ \displaystyle\frac{3}{4} \ }\)である
これより\(\small{ \ z=\displaystyle\frac{3}{4}-2i \ }\)

解答2はゴリゴリ計算する方法だよね。それに対して解答1と解答4は共役の性質を利用する方法。解答3は図形的性質を利用する方法。

こんな問題でも様々な解き方があるよね。計算して解くのか図形の性質を利用するか、どの解き方で解くのかっていうのは、問題によって解きやすさも変わってくる。

できればいろいろな方法で問題を解いて複素数平面の解き方、考え方をマスターしてほしい。

Point 複素数平面とその基本

①複素数の計算（絶対値や和差）をマスターする
②共役複素数の性質を覚える
③計算の利用や複素数平面の利用など解き方について考える

問題解答1解答2解答3解答4

複素数\(\small{ \ z_1, \ z_2 \ }\)が\(\small{ \ |z_1|=|z_2|=|z_1+z_2|=1 \ }\)を満たすとき、\(\small{ \ |z_1-z_2| \ }\)を求めよ。

\(\small{ \ |z_1|^2=z_1\bar{z_1}=1 \ }\)
\(\small{ \ |z_2|^2=z_2\bar{z_2}=1 \ }\)
\(\small{ \ |z_1+z_2|^2=(z_1+z_2)(\overline{z_1+z_2})=1 \ }\)
\(\small{ \ z_1\bar{z_1}+\ z_1\bar{z_2}+\ z_2\bar{z_1}+\ z_2\bar{z_2}=1 \ }\)
\(\small{ \ z_1\bar{z_2}+\ z_2\bar{z_1}=-1 \ }\)
\(\small{\begin{eqnarray} \ |z_1-z_2|^2&=&(z_1-z_2)(\overline{z_1-z_2})\\[3pt] &=&z_1\bar{z_1}-\ z_1\bar{z_2}-\ z_2\bar{z_1}+\ z_2\bar{z_2}\\[3pt] &=&3 \ \end{eqnarray}}\)
\(\small{ \ \therefore |z_1-z_2|=\sqrt{3} \ }\)

\(\small{ \ z_1=a+bi, \ z_2=c+di \ }\)とする
ただし、\(\small{ \ a, \ b, \ c, \ d \ }\)は実数とする
\(\small{ \ |z_1|^2=a^2+b^2=1 \ }\)
\(\small{ \ |z_2|^2=c^2+d^2=1 \ }\)
\(\small{ \ z_1+z_2=(a+c)+(b+d)i \ }\)より
\(\small{ \ |z_1+z_2|^2=(a+c)^2+(b+d)^2=1 \ }\)
\(\small{ \ a^2+b^2+c^2+d^2+2ac+2bd=1 \ }\)
\(\small{ \ 2ac+2bd=-1 \ }\)
\(\small{ \ z_1+z_2=(a-c)+(b-d)i \ }\)より

\(\small{\begin{eqnarray} \ |z_1-z_2|^2&=&(a-c)^2+(b-d)^2\\[3pt] &=&a^2+b^2+c^2+d^2-2ac-2bd\\[3pt] &=&3 \ \end{eqnarray}}\)

\(\small{ \ \therefore |z_1-z_2|=\sqrt{3} \ }\)

点\(\small{ \ \mathrm{A}(z_1) \ }\)、点\(\small{ \ \mathrm{B}(z_2) \ }\)、点\(\small{ \ \mathrm{C}(-z_1-z_2) \ }\)とする
\(\small{ \ |z_1|=|z_2|=|z_1+z_2|=1 \ }\)より
原点は\(\small{ \ \triangle \mathrm{ABC} \ }\)の外心になる
また\(\small{ \ \displaystyle\frac{z_1+z_2+(-z_1-z_2)}{3}=0 \ }\)より
原点は\(\small{ \ \triangle \mathrm{ABC} \ }\)の重心になる
よって\(\small{ \ \triangle \mathrm{ABC} \ }\)は原点を中心とする半径\(\small{ \ 1 \ }\)の円に内接する正三角形である

よって正弦定理から
\(\small{\begin{eqnarray} \ |z_1-z_2|&=&\mathrm{AB}\\[3pt] &=&2\sin 60^{\circ}\\[3pt] &=&\sqrt{3} \ \end{eqnarray}}\)

\(\small{ \ |z_1|=1 \ }\)より
原点を中心とする半径\(\small{ \ 1 \ }\)の円周上に点\(\small{ \ \mathrm{A}(z_1) \ }\)をとる
\(\small{ \ |z_1|=|z_2|=|z_1+z_2|=1 \ }\)より点\(\small{ \ \mathrm{B}(z_2) \ }\)と点\(\small{ \ \mathrm{C}(z_1+z_2) \ }\)も同じ円周上にある
よって四角形\(\small{ \ \mathrm{OACB} \ }\)は平行四辺形になる
点\(\small{ \ \mathrm{B}(z_2) \ }\)と点\(\small{ \ \mathrm{C}(z_1+z_2) \ }\)は点\(\small{ \ \mathrm{A}(z_1) \ }\)に対して、図のような位置関係になければならない。

余弦定理より
\(\small{\begin{eqnarray} \ |z_1-z_2|^2&=&\mathrm{AB}^2\\[3pt] &=&1^2+1^2-2\cdot1\cdot1\cos 120^{\circ}\\[3pt] &=&3 \ \end{eqnarray}}\)
\(\small{ \ \therefore |z_1-z_2|=\sqrt{3} \ }\)

複素数平面の問題は大きく分けて
①\(\small{ \ z \ }\)のまま解く
②\(\small{ \ z=a+bi \ }\)として解く
③極形式\(\small{ \ z=r(\cos \theta+i\sin \theta) \ }\)で解く
④座標を利用して解く
⑤図形を利用して解く
がある。
基本的な問題こそいろいろな解き方でチャレンジしてみよう。応用問題を解くときにそれが活かされるからね。