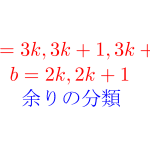こんにちは、リンス(@Lins016)です。
今回は倍数の証明について学習していこう。
倍数の証明方法
・\(\small{ \ n \ }\)が自然数のとき\(\small{ \ n(n+1)(2n+1) \ }\)は\(\small{ \ 6 \ }\)で割り切れることを証明せよ。
こんな感じの倍数の証明問題の基本的な考え方は\(\small{ \ 3 \ }\)つのパターンがある。どの証明の考え方も入試では絶対必要だから確実に押さえておこう。
①\(\small{ \ n \ }\)個の連続する自然数の積は\(\small{ \ n! \ }\)の倍数
②余りで分類してくくりだす
③合同式を利用する
連続する自然数の積
\(\small{ \ n \ }\)個の連続する自然数の積は\(\small{ \ n! \ }\)の倍数になるんだ。
これは以前の記事にしてるから、まずはこの記事を確認してほしい。
-

連続する自然数の積
連続する自然数の積がもつ因数の個数や性質などについて詳しく解説しています。
続きを見る
特に\(\small{ \ 3 \ }\)個の連続する自然数の積は\(\small{ \ 6 \ }\)の倍数になるってことはよく知られてるからね。
\(\small{ \ (n-1)n(n+1) \ }\)には少なくとも\(\small{ \ 1 \ }\)つは偶数が入っているし、\(\small{ \ 3 \ }\)の倍数も\(\small{ \ 1 \ }\)つあるからね。
倍数の問題では重要なヒントになるから確実に覚えておこう。
余りで分類する
例えば「ある\(\small{ \ n \ }\)の式\(\small{ \ f(n) \ }\)が\(\small{ \ 6 \ }\)の倍数であることを証明せよ。」って言われたら\(\small{ \ 6 \ }\)でくくって\(\small{ \ 6( \ \ \ \ \ \ \ ) \ }\)の形にして\(\small{ \ 6 \ }\)の倍数って証明したいよね。
でも\(\small{ \ 6 \ }\)でくくろうにも\(\small{ \ 6 \ }\)が出てこないとくくれないから、証明するの難しいよね。
だから\(\small{ \ 6 \ }\)を出しやすくするために、\(\small{ \ n \ }\)を\(\small{ \ 6 \ }\)で割った余りで分類するんだ。
\(\small{ \ n=6k \ }\),\(\small{ \ 6k+1 \ }\),\(\small{ \ 6k+2 \ }\),\(\small{ \ 6k+3 \ }\),\(\small{ \ 6k+4 \ }\),\(\small{ \ 6k+5 \ }\)ってすることで\(\small{ \ 6 \ }\)が出てくるから\(\small{ \ 6 \ }\)でくくりやすくなるよね。つまり\(\small{ \ 6 \ }\)の倍数って言いやすくなるんだ。
余りの分類については次の記事を確認しておこう。
-

整数の割り算と余りの分類
余りの分類を利用して整数を表す方法について詳しく解説しています。
続きを見る

合同式を利用する
余りで分類する方法と同じような考え方になるけど、合同式を利用して考える方法もある。
例えば倍数を証明したい\(\small{ \ n \ }\)の式が\(\small{ \ n^3-n \ }\)のような式なら余りで分類してもそこまで大変じゃないけど、\(\small{ \ n^5-n \ }\)なら\(\small{ \ 5 \ }\)乗するの大変だよね。だからそのときは合同式を使えば簡単に処理できる。
まずは合同式の使い方を次の記事で確認しておこう。
-

割り算の余りの性質と合同式
割り算の余りを利用した計算や合同式の基本について詳しく解説しています。
続きを見る
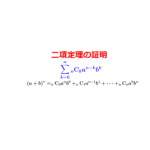
例えば、\(\small{ \ (6k+1)^5 \ }\)について考えてみよう。
これを展開すると
一番最後の項\(\small{ \ _{5}\mathrm{C}_{5}(6k)^{0}=1 \ }\)以外は\(\small{ \ 6 \ }\)の倍数だから\(\small{ \ (6k+1)^5 \ }\)を\(\small{ \ 6 \ }\)で割った余りは\(\small{ \ 1 \ }\)になるよね。
これを合同式で考えてみよう。
\(\small{ \ n=6k+1 \ }\)は\(\small{ \ n \equiv 1 \pmod 6 \ }\)になるよね。
だから\(\small{ \ n^3 \equiv 1^3\equiv 1 \pmod 6 \ }\)
合同式を使うことで簡単に計算できるってことを覚えておこう。

-

二項定理の証明
数学的帰納法を用いた二項定理の証明について詳しく解説しています。
続きを見る
\(\small{ \ n \ }\)が自然数のとき、\(\small{ \ n(n+1)(2n+1) \ }\)が\(\small{ \ 6 \ }\)の倍数であることを証明せよ。
\(\small{ \ 3 \ }\)つの連続する自然数の積は\(\small{ \ 6 \ }\)の倍数だから
\(\small{ \ n(n+1)(n+2) \ }\)も\(\small{ \ (n-1)n(n+1) \ }\)も\(\small{ \ 6 \ }\)の倍数である
よって\(\small{ \ n(n+1)(2n+1) \ }\)は\(\small{ \ 6 \ }\)の倍数である
\(\small{ \ n(n+1) \ }\)は連続する自然数の積だから\(\small{ \ 2 \ }\)の倍数である
よって\(\small{ \ n(n+1)(2n+1) \ }\)が\(\small{ \ 3 \ }\)の倍数になることを示せばよい。
(i)\(\small{ \ n=3k \ }\)のとき
\(\small{\begin{align}&n(n+1)(2n+1)\\[3pt]
&=3k(3k+1)(6k+1) \ \end{align}}\)
よって\(\small{ \ 3 \ }\)の倍数である。
(ii)\(\small{ \ n=3k+1 \ }\)のとき
\(\small{\begin{align} &n(n+1)(2n+1)\\[3pt]
&=(3k+1)(3k+2)(6k+3)\\[3pt]
&=3(3k+1)(3k+2)(2k+1) \ \end{align}}\)
よって\(\small{ \ 3 \ }\)の倍数である。
(ii)\(\small{ \ n=3k+2 \ }\)のとき
\(\small{\begin{align}&n(n+1)(2n+1)\\[3pt]
&=(3k+2)(3k+3)(6k+5)\\[3pt]
&=3(3k+2)(k+1)(6k+5) \ \end{align}}\)
よって\(\small{ \ 3 \ }\)の倍数である。
よって\(\small{ \ n(n+1)(2n+1) \ }\)は\(\small{ \ 6 \ }\)の倍数である
Point 倍数の証明
①連続する自然数の積を利用する
②余りの分類を利用する
③合同式を利用する
\(\small{ \ N \ }\)は十進法で表された\(\small{ \ 4 \ }\)桁の自然数であり、千の位の数が\(\small{ \ a \ }\)、百の位の数が\(\small{ \ b \ }\)、十の位の数が\(\small{ \ c \ }\)、一の位の数が\(\small{ \ d \ }\)である。
(1)\(\small{ \ a-b+c-d \ }\)が\(\small{ \ 11 \ }\)の倍数なら\(\small{ \ N \ }\)は\(\small{ \ 11 \ }\)の倍数であることを示せ。
(2)\(\small{ \ N \ }\)が\(\small{ \ 11 \ }\)の倍数なら\(\small{ \ N^5-N \ }\)は\(\small{ \ 55 \ }\)の倍数であることを示せ。
(1)
(ただし、\(\small{ \ K \ }\)は整数)
これより\(\small{ \ a-b+c-d \ }\)が\(\small{ \ 11 \ }\)の倍数なら\(\small{ \ N \ }\)は\(\small{ \ 11 \ }\)の倍数である
(2)
\(\small{ \ N \ }\)が\(\small{ \ 11 \ }\)の倍数のとき\(\small{ \ N^5-N=N(N^4-1) \ }\)より\(\small{ \ N^5-N \ }\)は\(\small{ \ 11 \ }\)の倍数である
よって\(\small{ \ N^5-N \ }\)が\(\small{ \ 55 \ }\)の倍数であることを示すには、\(\small{ \ N^5-N \ }\)が\(\small{ \ 5 \ }\)の倍数であることを示せばよい
ここで\(\small{ \ N^5-N=N(N-1)(N+1)(N^2+1) \ }\)と変形できる
\(\small{ \ N=11k \ }\)(\(\small{ \ k \ }\)は整数)とする
(i)\(\small{ \ k=5l \ }\)のとき
\(\small{ \ N \ }\)は\(\small{ \ 5 \ }\)の倍数だから\(\small{ \ N^5-N \ }\)は\(\small{ \ 5 \ }\)の倍数である
(ii)\(\small{ \ k=5l+1 \ }\)のとき
\(\small{\begin{eqnarray} \ N-1&=&11(5l+1)-1\\[3pt]
&=&55l-10 \ \end{eqnarray}}\)
これは\(\small{ \ 5 \ }\)の倍数だから\(\small{ \ N^5-N \ }\)は\(\small{ \ 5 \ }\)の倍数である
(iii)\(\small{ \ k=5l+2 \ }\)のとき
\(\small{\begin{eqnarray} \ N^2+1&=&11^2(5l+2)^2+1\\[3pt]
&=&11^2(25l^2+20l)+485 \ \end{eqnarray}}\)
これは\(\small{ \ 5 \ }\)の倍数だから\(\small{ \ N^5-N \ }\)は\(\small{ \ 5 \ }\)の倍数である
(iv)\(\small{ \ k=5l+3 \ }\)のとき
\(\small{\begin{eqnarray} \ N^2+1&=&11^2(5l+3)^2+1\\[3pt]
&=&11^2(25l^2+30l)+1090 \ \end{eqnarray}}\)
これは\(\small{ \ 5 \ }\)の倍数だから\(\small{ \ N^5-N \ }\)は\(\small{ \ 5 \ }\)の倍数である
(v)\(\small{ \ k=5l+4 \ }\)のとき
\(\small{\begin{eqnarray} \ N+1&=&11(5l+4)+1\\[3pt]
&=&55l+45 \ \end{eqnarray}}\)
これは\(\small{ \ 5 \ }\)の倍数だから\(\small{ \ N^5-N \ }\)は\(\small{ \ 5 \ }\)の倍数である
(i)〜(v)より\(\small{ \ N \ }\)が\(\small{ \ 11 \ }\)の倍数なら\(\small{ \ N^5-N \ }\)は\(\small{ \ 55 \ }\)の倍数である
(1)
\(\small{ \ N=10^3a+10^2b+10c+d \ }\)と表せる
ここで\(\small{ \ 10 \equiv -1 \pmod {11} \ }\)より
\(\small{ \ 10^3a \equiv (-1)^3a\equiv-a \pmod {11}\cdots① \ }\)
\(\small{ \ 10^2b \equiv (-1)^2b\equiv b \pmod {11}\cdots② \ }\)
\(\small{ \ 10c \equiv -c \pmod {11}\cdots③ \ }\)
\(\small{ \ d \equiv d \pmod {11}\cdots④ \ }\)
\(\small{ \ ①+②+③+④ \ }\)
\(\small{ \ 10^3a+10^2b+10c+d \equiv -a+b-c+d \pmod {11} \ }\)
つまり\(\small{ \ N \ }\)を\(\small{ \ 11 \ }\)で割った余りは\(\small{ \ -a+b-c+d \ }\)より
\(\small{ \ a-b+c-d \ }\)が\(\small{ \ 11 \ }\)の倍数なら\(\small{ \ N \ }\)は\(\small{ \ 11 \ }\)の倍数である
(2)
(i)\(\small{ \ N \equiv 0 \pmod 5 \ }\)のとき
\(\small{ \ N^5-N \equiv 0 \pmod 5 \ }\)より\(\small{ \ N^5-N \ }\)は\(\small{ \ 5 \ }\)の倍数
(ii)\(\small{ \ N \equiv 1 \pmod 5 \ }\)のとき
\(\small{ \ N^5 \equiv 1 \pmod 5 \ }\)
\(\small{ \ N^5-N \equiv 0 \pmod 5 \ }\)より\(\small{ \ N^5-N \ }\)は\(\small{ \ 5 \ }\)の倍数
(iii)\(\small{ \ N \equiv 2 \pmod 5 \ }\)のとき
\(\small{ \ N^5 \equiv 2^5 \equiv 2 \pmod 5 \ }\)
\(\small{ \ N^5-N \equiv 0 \pmod 5 \ }\)より\(\small{ \ N^5-N \ }\)は\(\small{ \ 5 \ }\)の倍数
(iv)\(\small{ \ N \equiv 3 \pmod 5 \ }\)のとき
\(\small{ \ N^2 \equiv 9 \equiv -1 \pmod 5 \ }\)
\(\small{ \ N^5 \equiv (-1)^2\cdot3 \equiv 3 \pmod 5 \ }\)
\(\small{ \ N^5-N \equiv 0 \pmod 5 \ }\)より\(\small{ \ N^5-N \ }\)は\(\small{ \ 5 \ }\)の倍数
(v)\(\small{ \ N \equiv 4 \pmod 5 \ }\)のとき
\(\small{ \ N \equiv 4 \equiv -1 \pmod 5 \ }\)
\(\small{ \ N^5 \equiv (-1)^5 \equiv -1\equiv 4 \pmod 5 \ }\)
\(\small{ \ N^5-N \equiv 0 \pmod 5 \ }\)より\(\small{ \ N^5-N \ }\)は\(\small{ \ 5 \ }\)の倍数
(i)~(v)より\(\small{ \ N^5-N \ }\)は\(\small{ \ 5 \ }\)の倍数である
また\(\small{ \ N^5-N=N(N^4-1) \ }\)と変形できるので\(\small{ \ N \ }\)が\(\small{ \ 11 \ }\)の倍数のとき\(\small{ \ N^5-N \ }\)は\(\small{ \ 55 \ }\)の倍数である