こんにちは、リンス(@Lins016)です。
今回は連続する自然数の積について学習していこう。
連続する自然数の積
連続する自然数の積の問題って実は結構あって、階乗を利用した\(\small{ \ n! \ }\)なんかも連続する\(\small{ \ n \ }\)個の自然数の積だからね。
今回はこの連続する自然数の積の問題を解く上で必要な知識について話をしていくよ。
①連続する\(\small{ \ n \ }\)個の自然数の積は\(\small{ \ n! \ }\)の倍数である
②\(\small{ \ n! \ }\)を素因数分解したとき素因数\(\small{ \ p \ }\)の数は\(\small{ \ n \ }\)を\(\small{ \ p, \ p^2, \ p^3,\cdots \ }\)で割った商をすべて足す
n個の連続する自然数の積
\(\small{ \ n \ }\)個の連続する自然数の積は\(\small{ \ n! \ }\)の倍数なんだ。
今回はこれについてを考えてみよう。
自然数\(\small{ \ m \ }\)から連続する\(\small{ \ n \ }\)個の自然数の積は
\(\small{ \ \overbrace{m\cdot(m+1)\cdot(m+2)\cdots\cdot(m+n-1)}^{ n個 } \ }\)になる。
これに\(\small{ \ (m-1)! \ }\)をかけると
=(m+n-1)! \ }\)
だから
ここで上の式を\(\small{ \ n! \ }\)で割ると
\(\small{\begin{array}{l} \ \displaystyle\frac{m\cdot(m+1)\cdot(m+2)\cdots\cdot(m+n-1)}{n!}\\
=\displaystyle\frac{(m+n-1)!}{n!(m-1)!}\\
= \ _{m+n-1}\mathrm{C}_{m-1}\\
= \ _{m+n-1}\mathrm{C}_{n} \ \end{array}}\)
右辺は\(\small{ \ m+n-1 \ }\)個の中から\(\small{ \ n \ }\)個選ぶ(または\(\small{ \ m-1 \ }\)個選ぶ)組合せの数だから自然数だよね。
だから\(\small{ \ \displaystyle\frac{m\cdot(m+1)\cdot(m+2)\cdots\cdot(m+n-1)}{n!} \ }\)は自然数になって、
\(\small{ \ m\cdot(m+1)\cdot(m+2)\cdots\cdot(m+n-1) \ }\)は\(\small{ \ n! \ }\)の倍数になるんだ。
(1)\(\small{ \ n \ }\)が整数のとき\(\small{ \ n(n-1)(2n-1) \ }\)は\(\small{ \ 6 \ }\)の倍数であることを証明せよ。
(2)\(\small{ \ 3 \ }\)つの連続する奇数の\(\small{ \ 2 \ }\)乗の和に\(\small{ \ 1 \ }\)を加えた数は\(\small{ \ 12 \ }\)の倍数であるが、\(\small{ \ 24 \ }\)の倍数でないことを証明せよ。
(1)
=n(n-1)(n+1+n-2)\\
=(n-1)n(n+1)+(n-2)(n-1)n \ \end{array}}\)
\(\small{ \ 3 \ }\)つの連続する自然数の積は\(\small{ \ 6 \ }\)の倍数より
\(\small{ \ n \ }\)が整数のとき\(\small{ \ n(n-1)(2n-1) \ }\)は\(\small{ \ 6 \ }\)の倍数である
(2)\(\small{ \ 3 \ }\)つの連続する奇数は整数\(\small{ \ k \ }\)を用いて\(\small{ \ 2k-1, \ 2k+1, \ 2k+3 \ }\)とおける
=12k^2+12k+12\\
=12(k^2+k+1)\\
=12\left\{k(k+1)+1\right\} \ \end{array}}\)
\(\small{ \ 2 \ }\)つの連続する自然数の積は\(\small{ \ 2 \ }\)の倍数より\(\small{ \ k(k+1)+1 \ }\)は奇数である
よって\(\small{ \ 3 \ }\)つの連続する奇数の\(\small{ \ 2 \ }\)乗の和に\(\small{ \ 1 \ }\)を加えた数は\(\small{ \ 12 \ }\)の倍数であるが、\(\small{ \ 24 \ }\)の倍数でない

確かに\(\small{ \ 2 \ }\)つの連続する自然数は奇数と偶数になるから積は偶数になるよね。\(\small{ \ 3 \ }\)つの連続する自然数も少なくとも\(\small{ \ 1 \ }\)つ\(\small{ \ 2 \ }\)の倍数が入ってるし、\(\small{ \ 1 \ }\)つ\(\small{ \ 3 \ }\)の倍数が入ってるから\(\small{ \ 6 \ }\)の倍数になるって言えるよね
\(\small{ \ 6 \ }\)の倍数であるって証明は、\(\small{ \ 6 \ }\)で割った余りで分類して証明することもできるけど、それだとあまりのパターンが\(\small{ \ 0~5 \ }\)まであってちょっと面倒だよね。
連続する自然数の積と素因数の個数
次に\(\small{ \ n! \ }\)の中に含まれる素因数の個数について考えていこう。
\(\small{ \ n! \ }\)のまま考えると分かりにくいから、具体的に\(\small{ \ 100! \ }\)を素因数分解したとき、素因数\(\small{ \ 2 \ }\)は何個あるか調べてみよう。
\(\small{ \ 1 \ }\)から\(\small{ \ 100 \ }\)までの\(\small{ \ 100 \ }\)個の整数のうち
①少なくとも\(\small{ \ 2 \ }\)で\(\small{ \ 1 \ }\)回割り切れるのは
\(\small{ \ 100\div2=50 \ }\)個
②少なくとも\(\small{ \ 2^2=4 \ }\)で\(\small{ \ 1 \ }\)回割り切れるのは
\(\small{ \ 100\div4=25 \ }\)個
③少なくとも\(\small{ \ 2^3=8 \ }\)で\(\small{ \ 1 \ }\)回割り切れるのは
\(\small{ \ 100\div8=12 \ }\)あまり\(\small{ \ 4 \ }\)より\(\small{ \ 12 \ }\)個
④少なくとも\(\small{ \ 2^4=16 \ }\)で\(\small{ \ 1 \ }\)回割り切れるのは
\(\small{ \ 100\div16=6 \ }\)あまり\(\small{ \ 4 \ }\)より\(\small{ \ 6 \ }\)個
⑤少なくとも\(\small{ \ 2^5=32 \ }\)で\(\small{ \ 1 \ }\)回割り切れるのは
\(\small{ \ 100\div32=3 \ }\)あまり\(\small{ \ 4 \ }\)より\(\small{ \ 3 \ }\)個
⑥少なくとも\(\small{ \ 2^6=64 \ }\)で\(\small{ \ 1 \ }\)回割り切れるのは
\(\small{ \ 100\div64=1 \ }\)あまり\(\small{ \ 36 \ }\)より\(\small{ \ 1 \ }\)個
①~⑥より\(\small{ \ 100! \ }\)は素因数\(\small{ \ 2 \ }\)を
\(\small{ \ 50+25+12+6+3+1=97 \ }\)個持つっていえるんだ。
これは下の図をみてもらうといいかな。
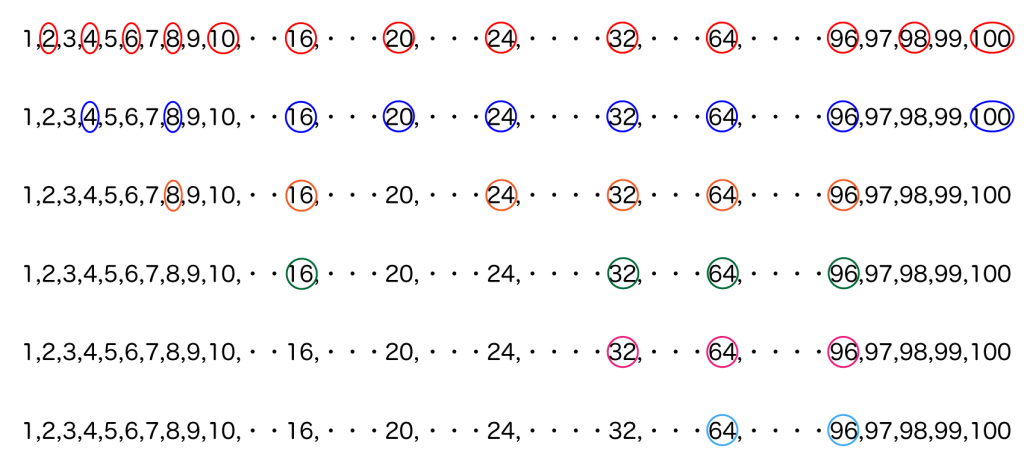
例えば\(\small{ \ 16 \ }\)は\(\small{ \ 2^4 \ }\)だから素因数\(\small{ \ 2 \ }\)を\(\small{ \ 4 \ }\)個持つって言えるよね。
この\(\small{ \ 4 \ }\)個は①の\(\small{ \ 2 \ }\)で\(\small{ \ 1 \ }\)回割れる\(\small{ \ 50 \ }\)個(赤〇で囲まれた数)のうちの\(\small{ \ 1 \ }\)個と、②の\(\small{ \ 2^2 \ }\)で\(\small{ \ 1 \ }\)回割れる\(\small{ \ 25 \ }\)個(青〇で囲まれた数)のうちの\(\small{ \ 1 \ }\)個と、③の\(\small{ \ 2^3 \ }\)で\(\small{ \ 1 \ }\)回割れる\(\small{ \ 12 \ }\)個(オレンジ〇で囲まれた数)のうちの\(\small{ \ 1 \ }\)個と、④の\(\small{ \ 2^4 \ }\)で\(\small{ \ 1 \ }\)回割れる\(\small{ \ 6 \ }\)個(緑〇で囲まれた数)のうちの\(\small{ \ 1 \ }\)個の合計\(\small{ \ 4 \ }\)個っていう風に数えているんだ。
だから\(\small{ \ 2^1 \ }\)から\(\small{ \ 2^2, \ 2^3,\cdots \ }\)って順に指数を大きくして\(\small{ \ 100 \ }\)を割ったときの商を足せば素因数\(\small{ \ 2 \ }\)の個数になるんだ。
つまり上の図の〇の数が素因数\(\small{ \ 2 \ }\)の個数ってことだからね。
\(\small{ \ 1 \ }\)から\(\small{ \ 300 \ }\)までの\(\small{ \ 300 \ }\)個の自然数の積\(\small{ \ N=1\cdot2\cdot3\cdots299\cdot300 \ }\)を計算すると末尾には\(\small{ \ 0 \ }\)が連続して何個並ぶか答えよ。
\(\small{ \ N \ }\)の末尾にいくつ続けて\(\small{ \ 0 \ }\)が並ぶかは、\(\small{ \ N \ }\)を因数分解したとき、因数\(\small{ \ 10 \ }\)を何個持つかということで、\(\small{ \ 10=2\times5 \ }\)より\(\small{ \ N \ }\)を素因数分解したとき、素因数\(\small{ \ 5 \ }\)を何個持つかを調べればよい。
\(\small{ \ 300\div5=60 \ }\)
\(\small{ \ 300\div5^2=12 \ }\)
\(\small{ \ 300\div5^3=2 \ }\)あまり\(\small{ \ 50 \ }\)
よって\(\small{ \ 60+12+2=74 \ }\)個連続で\(\small{ \ 0 \ }\)が並ぶ

Point 連続する自然数の積
①連続する\(\small{ \ n \ }\)個の自然数の積は\(\small{ \ n! \ }\)の倍数である
②\(\small{ \ n! \ }\)を素因数分解したとき素因数\(\small{ \ p \ }\)の数は\(\small{ \ n \ }\)を\(\small{ \ p, \ p^2, \ p^3,\cdots \ }\)で割った商をすべて足した数になる
\(\small{ \ 30! \ }\)について答えよ。
(1)\(\small{ \ 30! \ }\)の一の位は\(\small{ \ 0 \ }\)である。ここから始めて十の位、百の位と順に左に見ていく。最初に\(\small{ \ 0 \ }\)でない数字が現れるまでに連続していくつの\(\small{ \ 0 \ }\)が並ぶか答えよ。
(2)(1)において、最初に現れる\(\small{ \ 0 \ }\)でない数字はいくつであるか理由とともに答えよ。
\(\small{ \ 30! \ }\)の末尾にいくつ続けて\(\small{ \ 0 \ }\)が並ぶかは、\(\small{ \ 30! \ }\)を素因数分解したとき素因数\(\small{ \ 5 \ }\)を何個持つかを調べればよい。
\(\small{ \ 30\div5=6 \ }\)
\(\small{ \ 30\div5^2=1 \ }\)あまり\(\small{ \ 5 \ }\)
よって\(\small{ \ 6+1=7 \ }\)個連続で\(\small{ \ 0 \ }\)が並ぶ
(2)\(\small{ \ 30! \ }\)を素因数分解すると
となる。
(1)より\(\small{ \ c=7 \ }\)
\(\small{ \ a \ }\)について
\(\small{ \ 30\div2=15 \ }\)
\(\small{ \ 30\div2^2=7 \ }\)あまり\(\small{ \ 2 \ }\)
\(\small{ \ 30\div2^3=3 \ }\)あまり\(\small{ \ 6 \ }\)
\(\small{ \ 30\div2^4=1 \ }\)あまり\(\small{ \ 14 \ }\)
よって\(\small{ \ a=15+7+3+1=26 \ }\)
\(\small{ \ b \ }\)について
\(\small{ \ 30\div3=10 \ }\)
\(\small{ \ 30\div3^2=3 \ }\)あまり\(\small{ \ 3 \ }\)
\(\small{ \ 30\div3^3=1 \ }\)あまり\(\small{ \ 3 \ }\)
よって\(\small{ \ b=10+3+1=14 \ }\)
\(\small{ \ d \ }\)について
\(\small{ \ 30\div7=4 \ }\)あまり\(\small{ \ 2 \ }\)
よって\(\small{ \ d=4 \ }\)
\(\small{ \ e \ }\)について
\(\small{ \ 30\div11=2 \ }\)あまり\(\small{ \ 8 \ }\)
よって\(\small{ \ e=2 \ }\)
\(\small{ \ f \ }\)について
\(\small{ \ 30\div13=2 \ }\)あまり\(\small{ \ 4 \ }\)
よって\(\small{ \ f=2 \ }\)
\(\small{ \ g \ }\)について
\(\small{ \ 30\div17=1 \ }\)あまり\(\small{ \ 13 \ }\)
よって\(\small{ \ g=1 \ }\)
\(\small{ \ h \ }\)について
\(\small{ \ 30\div19=1 \ }\)あまり\(\small{ \ 11 \ }\)
よって\(\small{ \ h=1 \ }\)
\(\small{ \ i \ }\)について
\(\small{ \ 30\div23=1 \ }\)あまり\(\small{ \ 7 \ }\)
よって\(\small{ \ h=1 \ }\)
\(\small{ \ j \ }\)について
\(\small{ \ 30\div29=1 \ }\)あまり\(\small{ \ 1 \ }\)
よって\(\small{ \ h=1 \ }\)
&=&10^7\times2^{19}\times3^{14}\times7^{4}\times11^2\times13^2\times17\times19\times23\times29 \ \end{eqnarray}}\)
ここで
\(\small{ \ 2^n \ }\)の下一桁は\(\small{ \ 2, \ 4, \ 8, \ 6 \ }\)の繰り返しだから\(\small{ \ 2^{19} \ }\)の下一桁は\(\small{ \ 8 \ }\)
\(\small{ \ 3^n \ }\)の下一桁は\(\small{ \ 3, \ 9, \ 7, \ 1 \ }\)の繰り返しだから\(\small{ \ 3^{14} \ }\)の下一桁は\(\small{ \ 9 \ }\)
\(\small{ \ 7^n \ }\)の下一桁は\(\small{ \ 7, \ 9, \ 3, \ 1 \ }\)の繰り返しだから\(\small{ \ 7^{4} \ }\)の下一桁は\(\small{ \ 1 \ }\)
よって
の下一桁の数は
\(\small{ \ 8\times9\times1\times1\times9\times7\times9\times3\times9 \ }\)の下一桁の数に等しい
よって求める数は\(\small{ \ 8 \ }\)である


