こんにちは、リンス(@Lins016)です。
今回はユークリッドの互除法と一次不定方程式について学習していこう。
ユークリッドの互除法と一次不定方程式
ユークリッドの互除法については前回学習したから、それは理解しているって前提で進めていくね。だからユークリッドの互除法についての記事を確認していない人は一度確認してから勉強するようにしよう。
方程式っていうと解を求める式のことだよね。これに不定って漢字をつけて、不定方程式って言われると不定って漢字から何か定まらないのかなって思うよね。
まさにその通りで、不定方程式っていうのは式の数より未知数の数が多い方程式のことで、未知数の方が多いから解が一つに定まらないよね。
ただ「整数を解に持つ」って条件がつくと未知数の方が多くても解を求めることができるんだ。
特に高校数学ではこの整数を未知数に持つ方程式のことを不定方程式って呼んでる。
一次不定方程式っていうのは求める解の文字(未知数)が\(\small{ \ 1 \ }\)次の項になっている不定方程式のことだからね。
自然数\(\small{ \ a, \ b \ }\)が互いに素なら
\(\small{ \ ax+by=1 \ }\)を満たす整数\(\small{ \ x, \ y \ }\)が存在する。
したがって任意の整数\(\small{ \ c \ }\)について
\(\small{ \ ax+by=c \ }\)を満たす整数\(\small{ \ x, \ y \ }\)が存在する。
ユークリッドの互除法と互いに素
\(\small{ \ ax+by=1 \ }\)の形の一次不定方程式を解くとき、\(\small{ \ x, \ y \ }\)が整数なら\(\small{ \ a \ }\)と\(\small{ \ b \ }\)が互いに素じゃないといけないんだ。大切なことだから覚えておこう。
例えば\(\small{ \ a=2, \ b=4 \ }\)だと\(\small{ \ 2x+4y=1 \ }\)になって左辺は\(\small{ \ 2(x+2y) \ }\)って\(\small{ \ a=2 \ }\)と\(\small{ \ b=4 \ }\)の最大公約数\(\small{ \ 2 \ }\)でくくれるから\(\small{ \ x, \ y \ }\)が整数のとき\(\small{ \ 2 \ }\)の倍数になるよね。
でも右辺は\(\small{ \ 1 \ }\)だから、これを満たす整数\(\small{ \ x, \ y \ }\)は存在しないんだ。
一般化すると\(\small{ \ a, \ b \ }\)の最大公約数を\(\small{ \ g \ }\)とすると\(\small{ \ a=a'g, \ b=b'g \ }\)(ただし、\(\small{ \ a', \ b' \ }\)は互いに素)っておけて、\(\small{ \ ax+by=1 \ }\)は\(\small{ \ a'gx+b'gy=1 \ }\)になるから\(\small{ \ g(a'x+b'y)=1 \ }\)
つまり\(\small{ \ x, \ y \ }\)が整数だと\(\small{ \ a'x+b'y \ }\)も\(\small{ \ g \ }\)も整数だから、\(\small{ \ g=1 \ }\)じゃないと成り立たないよね。
だから\(\small{ \ ax+by=1 \ }\)の一次不定方程式を解くとき、\(\small{ \ x, \ y \ }\)が整数なら\(\small{ \ a \ }\)と\(\small{ \ b \ }\)が互いに素じゃないといけないんだ。
ユークリッドの互除法を利用した一次不定方程式の解の求め方
じゃあ次に「\(\small{ \ 36x+25y=1 \ }\)を満たす整数\(\small{ \ x, \ y \ }\)を求めよ。」って問題を解く方法を見ながらユークリッドの互除法を使う方法を学習しよう。
\(\small{ \ 36 \ }\)と\(\small{ \ 25 \ }\)は互いに素だよね。\(\small{ \ 36=2^2\cdot3^2 \ }\)だし、\(\small{ \ 25=5^2 \ }\)だもんね。これは見てすぐ分かるよね。
まずは、この\(\small{ \ 36 \ }\)と\(\small{ \ 25 \ }\)をユークリッドの互除法を使って最大公約数が\(\small{ \ 1 \ }\)ってことを表してみよう。
ユークリッドの互除法より
\(\small{\begin{eqnarray} \ 36&=&25\times1+11\\
25&=&11\times2+3 \\
11&=&3\times3+2\\
3&=&2\times1+1\\
2&=&1\times2 \ \end{eqnarray}}\)
互いに素っていうのは最大公約数が\(\small{ \ 1 \ }\)になるってことなんだけど、余りが\(\small{ \ 1 \ }\)になればいいから実際最後の行まで計算しなくても\(\small{ \ 3=2\times1+1 \ }\)のところまで計算すればいいからね。
この互除法を利用して、この一次不定方程式を解いてみよう。
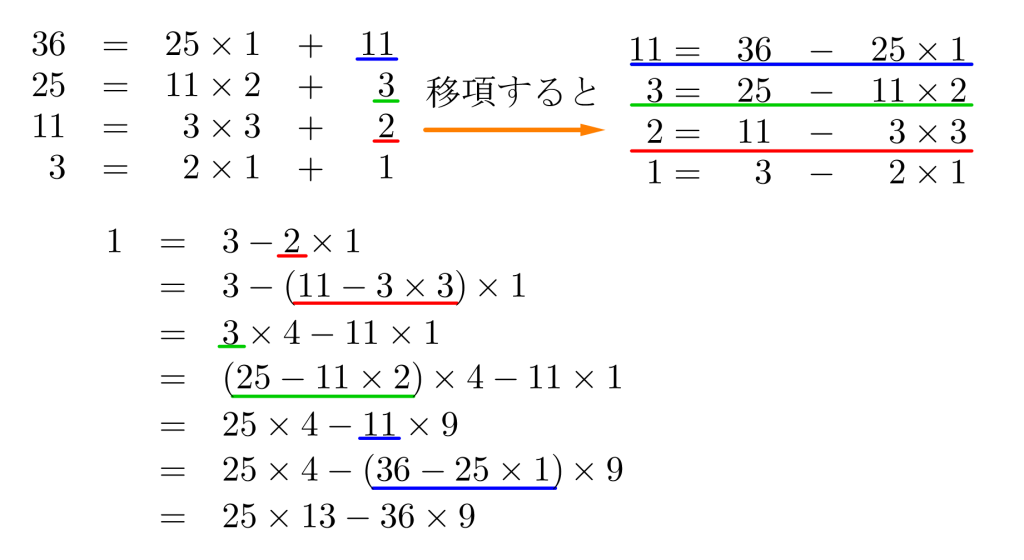
ユークリッドの互除法の式を移項して式をそれを逆にたどっていくんだ。
このときのコツはどの数を残したいかってことなんだ。\(\small{ \ 3 \ }\)と\(\small{ \ 11 \ }\)での組み合わせを\(\small{ \ 11 \ }\)と\(\small{ \ 25 \ }\)の組み合わせに変形する部分で確認してみよう。
\(\small{ \ 3 \ }\)を\(\small{ \ 11 \ }\)と\(\small{ \ 25 \ }\)で表すように変形したいから、\(\small{ \ 11 \ }\)と\(\small{ \ 25 \ }\)の係数に当たる\(\small{ \ 1 \ }\)と\(\small{ \ 2 \ }\)を\(\small{ \ 4 \ }\)倍するんだ。上の式変形では省略してるけど、丁寧に書くともっと計算する行は多くなるからね。
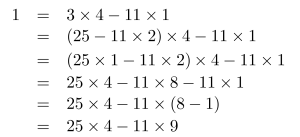
あとこの式は計算すると常に\(\small{ \ 1 \ }\)になるから式変形して整理した段階(\(\small{ \ 3\times4-11\times1 \ }\)や\(\small{ \ 25\times4-11\times9 \ }\))で\(\small{ \ 1 \ }\)になってるか確認しながら進めていこう。
一次不定方程式の応用
ユークリッドの互除法を使うと\(\small{ \ ax+by=1 \ }\)の形の一次不定方程式の\(\small{ \ 1 \ }\)つの解を求めることができたよね。だから次は少しこれを発展させた問題を考えてみよう。
まずは\(\small{ \ 36x+25y=3 \ }\)を満たす整数\(\small{ \ x, \ y \ }\)について考えてみよう。
\(\small{ \ x, \ y \ }\)の係数は互いに素だけど、右辺が\(\small{ \ 1 \ }\)じゃないタイプの問題ね。
この問題の場合もまずは\(\small{ \ 36x+25y=1 \ }\)について考えよう。
ユークリッドの互除法を利用して\(\small{ \ 36(-9)+25\cdot13=1 \ }\)になるのはさっき求めたよね。
\(\small{ \ 36x+25y=3 \ }\)は右辺が\(\small{ \ 3 \ }\)になっているから\(\small{ \ 36(-9)+25\cdot13=1 \ }\)を\(\small{ \ 3 \ }\)倍すればいいんだ。
ここで注意しておきたいのが\(\small{ \ x, \ y \ }\)の部分にあたる数を\(\small{ \ 3 \ }\)倍するってことなんだ。
つまり\(\small{ \ 36(-9)+25\cdot13=1 \ }\)を\(\small{ \ 3 \ }\)倍して\(\small{ \ 36(-27)+25\cdot39=3 \ }\)って変形するんだ。
これで\(\small{ \ x=-27, \ y=39 \ }\)って求めることができるよね。
間違えて\(\small{ \ x, \ y \ }\)の係数の\(\small{ \ 36 \ }\)や\(\small{ \ 25 \ }\)を\(\small{ \ 3 \ }\)倍しないように注意しよう。
次に\(\small{ \ 72x+50y=6 \ }\)について考えてみよう。まずは\(\small{ \ 72 \ }\)と\(\small{ \ 50 \ }\)が互いに素じゃないよね。でも右辺が\(\small{ \ 1 \ }\)じゃなくてこの\(\small{ \ 72 \ }\)と\(\small{ \ 50 \ }\)の最大公約数\(\small{ \ 2 \ }\)で\(\small{ \ 6 \ }\)も割れるからこの場合解になる整数\(\small{ \ x, \ y \ }\)は存在するんだ。
\(\small{ \ 72x+50y=6 \ }\)を両辺\(\small{ \ 2 \ }\)で割ると\(\small{ \ 36x+25y=3 \ }\)になるからさっきと同じで\(\small{ \ 36x+25y=1 \ }\)を求めて、解を出せばいいよね。つまりこの問題も結局は\(\small{ \ 36x+25y=3 \ }\)だから\(\small{ \ x=-27, \ y=39 \ }\)になるんだ。
\(\small{ \ ax+by=c \ }\)は\(\small{ \ a,b \ }\)の最大公約数を\(\small{ \ c \ }\)が約数に持てば整数\(\small{ \ x, \ y \ }\)が存在するって言えるからね。
次の式を満たす整数解を\(\small{ \ 1 \ }\)つ求めよ。
(1)\(\small{ \ 23x+41y=1 \ }\)
(2)\(\small{ \ 14x+16y=6 \ }\)
(3)\(\small{ \ 9x-13y=7 \ }\)
(1)ユークリッドの互除法より
\(\small{\begin{eqnarray} \ 41&=&23+18\\
23&=&18+5\\
18&=&3\times5+3\\
5&=&3+2\\
3&=&2+1 \ \end{eqnarray}}\)
これより
\(\small{\begin{eqnarray} \ 1&=&3-2\\
&=&3-(5-3)\\
&=&2\times3-5\\
&=&2\times(18-3\times5)-5\\
&=&2\times18-7\times5\\
&=&2\times18-7(23-18)\\
&=&9\times18-7\times23\\
&=&9(41-23)-7\times23\\
&=&9\times41-16\times23 \ \end{eqnarray}}\)
\(\small{ \ 23x+41y=1 \ }\)より
\(\small{ \ x=-16, \ y=9 \ }\)
(2)\(\small{ \ 14x+16y=6 \ }\)
両辺を\(\small{ \ 2 \ }\)で割ると
\(\small{ \ 7x+8y=3 \ }\)
\(\small{ \ 8=7+1 \ }\)より
\(\small{ \ 8\times1-7\times1=1 \ }\)
両辺を\(\small{ \ 3 \ }\)倍すると
\(\small{ \ 8\times3-7\times3=3 \ }\)
\(\small{ \ 7x+8y=3 \ }\)より
\(\small{ \ x=-3, \ y=3 \ }\)
(3)ユークリッドの互除法より
\(\small{\begin{eqnarray}13&=&9+4\\
9&=&2\times4+1 \ \end{eqnarray}}\)
これより
\(\small{\begin{eqnarray} \ 1&=&9-2\times4\\
&=&9-2(13-9)\\
&=&3\times9-2\times13 \ \end{eqnarray}}\)
\(\small{ \ \therefore9\times3+13\times(-2)=1 \ }\)
両辺を\(\small{ \ 7 \ }\)倍して
\(\small{ \ 9\times21+13\times(-14)=7 \ }\)
\(\small{ \ 9x-13y=7 \ }\)より
\(\small{ \ x=21, \ y=14 \ }\)

一次不定方程式の解き方
ユークリッドの互除法を利用して一次不定方程式の解を\(\small{ \ 1 \ }\)つ見つけることができるようになったけど、一次不定方程式の解は\(\small{ \ 1 \ }\)つじゃないんだ。
\(\small{ \ 36x+25y=1 \ }\)のすべての解について考えてみよう。
この式は\(\small{ \ y=-\displaystyle\frac{36}{25}x+\displaystyle\frac{1}{25} \ }\)って変形できるよね。
これって座標平面上でみると傾き\(\small{ \ -\displaystyle\frac{36}{25} \ }\)の直線だよね。
さっきユークリッドの互除法を利用して\(\small{ \ (x, \ y)=(-9, \ 13) \ }\)を求めたよね。だから直線\(\small{ \ y=-\displaystyle\frac{36}{25}x+\displaystyle\frac{1}{25} \ }\)は\(\small{ \ (x, \ y)=(-9, \ 13) \ }\)を通るって言えるよね。
そうなるとこの直線は傾き\(\small{ \ -\displaystyle\frac{36}{25} \ }\)だから\(\small{ \ x \ }\)軸方向に\(\small{ \ 25 \ }\)進めると\(\small{ \ y \ }\)軸方向に\(\small{ \ -36 \ }\)下がるってことになるよね。
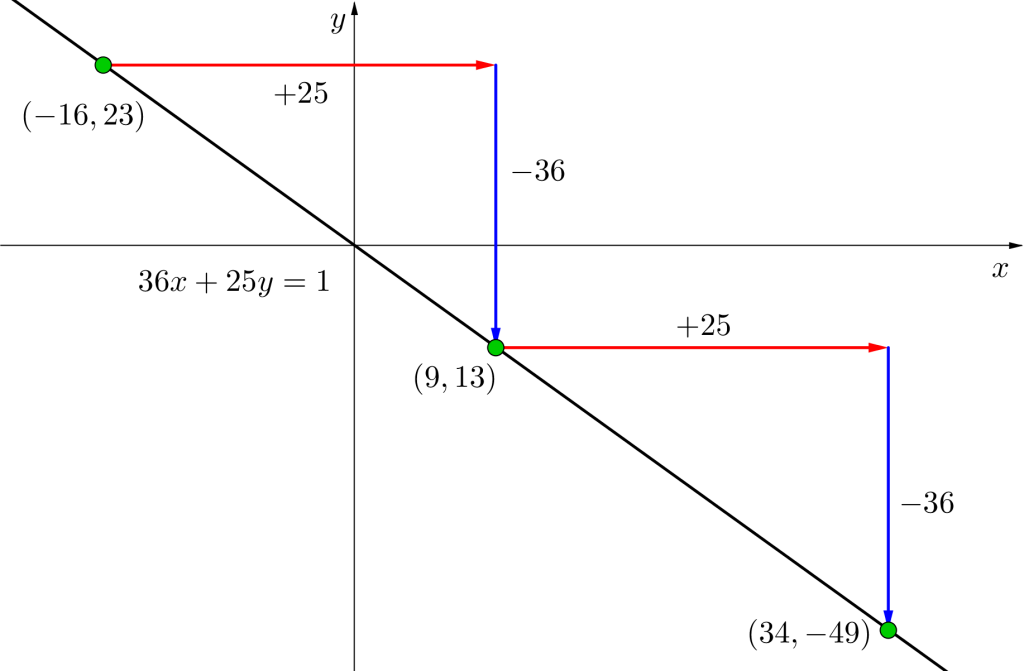
つまり格子点(\(\small{ \ x, \ y \ }\)ともに整数の点)は\(\small{ \ x \ }\)軸方向に\(\small{ \ 25 \ }\)ずつずれるたびに格子点が存在するって言えるんだ。
ってことはこの\(\small{ \ 36x+25y=1 \ }\)の解は無数にあるってことになるよね。
それじゃ\(\small{ \ 36x+25y=1 \ }\)を満たす無数の解を求めてみよう。まずはユークリッドの互除法を利用して解を一つ求めよう。
\(\small{ \ 36x+25y=1 \ }\)の場合は上で求めた\(\small{ \ 36\cdot(-9)+25\cdot13=1 \ }\)ってことね。
これを縦に並べて引くんだ。
\(\small{\begin{eqnarray} \ &&36x&+&25y&=&1\\
&-)&36\cdot(-9)&+&25\cdot13&=&1\\
\hline
&&36(x+9)&+&25(y-13)&=&0 \ \end{eqnarray}}\)
これを移行して
\(\small{ \ 36(x+9)=-25(y-13) \ }\)
ここで\(\small{ \ 36 \ }\)と\(\small{ \ 25 \ }\)は互いに素だから\(\small{ \ x+9 \ }\)は\(\small{ \ -25 \ }\)の倍数で、\(\small{ \ -(y-13) \ }\)は\(\small{ \ 36 \ }\)の倍数になるよね。つまり整数\(\small{ \ k \ }\)を利用すると
\(\small{ \ \begin{eqnarray}
\left\{
\begin{array}{l}
x+9=25k\\
-(y-13)=36k
\end{array}
\right.
\end{eqnarray} \ }\)
を満たすから
\(\small{ \ \begin{eqnarray}
\left\{
\begin{array}{l}
x=25k-9\\
y=-36k+13
\end{array}
\right.
\end{eqnarray} \ }\)
これが\(\small{ \ 36x+25y=1 \ }\)を満たすすべての整数解になるんだ。
\(\small{ \ 36(x+9)=-25(y-3) \ }\)の式を\(\small{ \ 36(x+9)=-25(y-3)=36\times25k \ }\)っておいて
\(\small{ \ \begin{eqnarray}
\left\{
\begin{array}{l}36(x+9)=36\times25k\\
-25(y-3)=36\times25k \end{array}
\right.
\end{eqnarray} \ }\)
から
\(\small{ \ \begin{eqnarray}
\left\{
\begin{array}{l}
x=25k-9\\
y=-36k+13
\end{array}
\right.
\end{eqnarray} \ }\)
を導いてもいいからね。
一次不定方程式の応用
次は右辺が\(\small{ \ 1 \ }\)じゃない\(\small{ \ 36x+25y=3 \ }\)を満たすすべての整数について考えてみよう。
これもまずはユークリッドの互除法を利用して\(\small{ \ 36x+25y=1 \ }\)を満たす整数解を\(\small{ \ 1 \ }\)つ求めよう。
\(\small{ \ 36x+25y=1 \ }\)の場合は上で求めた\(\small{ \ 36\cdot(-9)+25\cdot13=1 \ }\)ってことね。この式を右辺の\(\small{ \ 3 \ }\)に合わせるように\(\small{ \ 3 \ }\)倍して
\(\small{ \ 36\cdot(-27)+25\cdot39=3 \ }\)
これを元の式と縦に並べて引くと
\(\small{\begin{eqnarray} \ &&36x&+&25y&=&3\\
&-)&36\cdot(-27)&+&25\cdot39&=&3\\
\hline
&&36(x+27)&+&25(y-39)&=&0 \ \end{eqnarray}}\)
これを移行して
\(\small{ \ 36(x+27)=-25(y-39) \ }\)
これもさっきと同じで\(\small{ \ 36 \ }\)と\(\small{ \ 25 \ }\)は互いに素だから\(\small{ \ x+27 \ }\)は\(\small{ \ -25 \ }\)の倍数で、\(\small{ \ y-39 \ }\)は\(\small{ \ 36 \ }\)の倍数になるから整数\(\small{ \ k \ }\)を利用して
\(\small{ \ \begin{eqnarray}
\left\{
\begin{array}{l}
x+27=25k\\
-(y-39)=36k
\end{array}
\right.
\end{eqnarray} \ }\)
を満たすから
\(\small{ \ \begin{eqnarray}
\left\{
\begin{array}{l}
x=25k-27\\
y=-36k+39
\end{array}
\right.
\end{eqnarray} \ }\)
これが\(\small{ \ 36x+25y=3 \ }\)を満たすすべての整数解になるんだ。
次の式を満たす整数解を\(\small{ \ 1 \ }\)つ求めよ。
(1)\(\small{ \ 23x+41y=1 \ }\)
(2)\(\small{ \ 14x+16y=6 \ }\)
(3)\(\small{ \ 9x-13y=7 \ }\)
(1)ユークリッドの互除法より
\(\small{\begin{eqnarray} \ 41&=&23+18\\
23&=&18+5\\
18&=&3\times5+3\\
5&=&3+2\\
3&=&2+1 \ \end{eqnarray}}\)
これより
\(\small{\begin{eqnarray} \ 1&=&3-2\\
&=&3-(5-3)\\
&=&2\times3-5\\
&=&2\times(18-3\times5)-5\\
&=&2\times18-7\times5\\
&=&2\times18-7(23-18)\\
&=&9\times18-7\times23\\
&=&9(41-23)-7\times23\\
&=&9\times41-16\times23 \ \end{eqnarray}}\)
\(\small{\begin{eqnarray} \ &&23x&+&41y&=&1\\
&-)&23\cdot(-16)&+&41\cdot9&=&1\\
\hline
&&23(x+16)&+&41(y-9)&=&0 \ \end{eqnarray}}\)
\(\small{ \ \begin{eqnarray}
\left\{
\begin{array}{l}
x+16=41k\\
-(y-9)=23k
\end{array}
\right.
\end{eqnarray} \ }\)
(ただし、\(\small{ \ k \ }\)は整数)
を満たすから
\(\small{ \ \begin{eqnarray}
\left\{
\begin{array}{l}
x=41k-16\\
y=-23k+9
\end{array}
\right.
\end{eqnarray} \ }\)
(2)\(\small{ \ 14x+16y=6 \ }\)
両辺を\(\small{ \ 2 \ }\)で割ると
\(\small{ \ 7x+8y=3 \ }\)
\(\small{ \ 8=7+1 \ }\)より
\(\small{ \ 8\times1-7\times1=1 \ }\)
両辺を\(\small{ \ 3 \ }\)倍すると
\(\small{ \ 8\times3-7\times3=3 \ }\)
\(\small{\begin{eqnarray} \ &&7x&+&8y&=&3\\
&-)&7\cdot(-3)&+&8\cdot3&=&3\\
\hline
&&7(x+3)&+&8(y-3)&=&0 \ \end{eqnarray}}\)
\(\small{ \ \begin{eqnarray}
\left\{
\begin{array}{l}
x+3=8k\\
-(y-3)=7k
\end{array}
\right.
\end{eqnarray} \ }\)
(ただし、\(\small{ \ k \ }\)は整数)
を満たすから
\(\small{ \ \begin{eqnarray}
\left\{
\begin{array}{l}
x=8k-3\\
y=-7k+3
\end{array}
\right.
\end{eqnarray} \ }\)
(3)ユークリッドの互除法より
\(\small{\begin{eqnarray}13&=&9+4\\
9&=&2\times4+1 \ \end{eqnarray}}\)
これより
\(\small{\begin{eqnarray} \ 1&=&9-2\times4\\
&=&9-2(13-9)\\
&=&3\times9-2\times13 \ \end{eqnarray}}\)
\(\small{ \ \therefore9\times3+13\times(-2)=1 \ }\)
両辺を\(\small{ \ 7 \ }\)倍して
\(\small{ \ 9\times21+13\times(-14)=7 \ }\)
\(\small{\begin{eqnarray} \ &&9x&+&13y&=&7\\
&-)&9\cdot21&+&13\cdot(-14)&=&7\\
\hline
&&9(x-21)&+&13(y+14)&=&0 \ \end{eqnarray}}\)
\(\small{ \ \begin{eqnarray}
\left\{
\begin{array}{l}
x-21=13k\\
-(y+14)=9k
\end{array}
\right.
\end{eqnarray} \ }\)
(ただし、\(\small{ \ k \ }\)は整数)
を満たすから
\(\small{ \ \begin{eqnarray}
\left\{
\begin{array}{l}
x=13k+21\\
y=-9k-14
\end{array}
\right.
\end{eqnarray} \ }\)

Point ユークリッドの互除法と一次不定方程式
①ユークリッドの互除法を利用して整数解を一つ求める
②元の式と互除法を利用した式を引いてすべての解を求める

