ユークリッドの互除法と最大公約数

こんにちは、リンス(@Lins016)です。
今回はユークリッドの互除法について学習していこう。

ユークリッドの互除法と最大公約数

前に最大公約数について勉強したけど、そのときは素数で割り続ける連除法で、素因数分解してから最大公約数を求めたよね。

でも割れる素数（素因数）が大きい数の場合、簡単にその素因数を見つけることができないから、簡単に素因数分解できないんだ。

だから素因数分解をせずに最大公約数を見つける方法があるんだ。それをユークリッドの互除法っていうから、確実にこの方法を覚えよう。

ユークリッドの互除法の証明

自然数\(\small{ \ a, \ b \ }\)について\(\small{ \ a \ }\)を\(\small{ \ b \ }\)割ったときの商を\(\small{ \ q \ }\)余りを\(\small{ \ r \ }\)とすると\(\small{ \ a=bq+r \ }\)が成り立つよね。

これを前提にまずは\(\small{ \ a \ }\)と\(\small{ \ b \ }\)の最大公約数を\(\small{ \ g \ }\)とすると、\(\small{ \ a=a'g \ }\)、\(\small{ \ b=b'g \ }\)（\(\small{ \ a' \ }\)と\(\small{ \ b' \ }\)は互いに素）っておけるよね。

これを\(\small{ \ a=bq+r \ }\)に代入すると\(\small{ \ a'g=b'gq+r \ }\)ってなるから\(\small{ \ r=b'gq-a'g \ }\)って変形できるよね。

これを共通因数の\(\small{ \ g \ }\)でくくり出すと\(\small{ \ r=g(b'q-a') \ }\)ってなる。\(\small{ \ a', \ b', \ q \ }\)は自然数だから\(\small{ \ r \ }\)は\(\small{ \ g \ }\)を約数に持つって言えるよね。
つまりこれは\(\small{ \ a \ }\)と\(\small{ \ b \ }\)の最大公約数を\(\small{ \ \mathrm{gcd}(a,b) \ }\)って表すことにすると
\(\small{ \ \mathrm{gcd}(a,b)\leqq\mathrm{gcd}(b,r)\cdots① \ }\)ってことになるんだ。

今度は\(\small{ \ b \ }\)と\(\small{ \ r \ }\)の最大公約数を\(\small{ \ G \ }\)とすると、\(\small{ \ b=BG \ }\)、\(\small{ \ r=RG \ }\)（\(\small{ \ B \ }\)と\(\small{ \ R \ }\)は互いに素）っておけるよね。

これを\(\small{ \ a=bq+r \ }\)に代入すると\(\small{ \ a=BGq+RG \ }\)ってなるから\(\small{ \ a=G(Bq+R) \ }\)って変形できるよね。

\(\small{ \ B, \ R, \ q \ }\)は自然数だから\(\small{ \ a \ }\)は\(\small{ \ G \ }\)を約数に持つって言えるよね。
\(\small{ \ \mathrm{gcd}(a,b)\geqq\mathrm{gcd}(b,r)\cdots② \ }\)ってことになるんだ。
\(\small{ \ ①, \ ② \ }\)から\(\small{ \ \mathrm{gcd}(a,b)=\mathrm{gcd}(b,r) \ }\)になるよね。

つまり「\(\small{ \ a \ }\)と\(\small{ \ b \ }\)の最大公約数を\(\small{ \ g \ }\)とすると余り\(\small{ \ r \ }\)も\(\small{ \ g \ }\)を約数に持つ」と「\(\small{ \ b \ }\)と\(\small{ \ r \ }\)の最大公約数を\(\small{ \ G \ }\)とすると\(\small{ \ a \ }\)も\(\small{ \ G \ }\)を約数に持つ」を整理して、\(\small{ \ a \ }\)と\(\small{ \ b \ }\)の最大公約数と\(\small{ \ b \ }\)と\(\small{ \ r \ }\)の最大公約数は等しいってことになるんだ。

\(\small{ \ a \ }\)と\(\small{ \ b \ }\)の最大公約数を考えるより、\(\small{ \ b \ }\)と\(\small{ \ r \ }\)の最大公約数を考えるほうが楽だよね。だって\(\small{ \ a, \ b \ }\)に比べると\(\small{ \ b, \ r \ }\)の方が数が小さいからね。

むしろもっと考えてみると\(\small{ \ b \ }\)を\(\small{ \ r \ }\)割ったときの商を\(\small{ \ k \ }\)余りを\(\small{ \ s \ }\)とすると\(\small{ \ b=rk+s \ }\)が成り立つんだから、\(\small{ \ b \ }\)と\(\small{ \ r \ }\)の最大公約数を考えるより、\(\small{ \ r \ }\)と\(\small{ \ s \ }\)の最大公約数を考えるほうが楽だよね。つまりこの割り算を繰り返せば繰り返すほど、最大公約数を見つけたい\(\small{ \ 2 \ }\)つの数が小さくなっていくんだ。

最終的には余りがなくなるまで割り算をすれば、それが最大公約数になるんだ。

このやり方をユークリッドの互除法って言うから覚えておこう。

ユークリッドの互除法の計算

じゃあ次は実際にユークリッドの互除法を利用して最大公約数を求めてみよう。
\(\small{ \ 340 \ }\)と\(\small{ \ 265 \ }\)ぐらいのそこまで大きくない数だと連除法を使えばいいから、今回は\(\small{ \ 3059 \ }\)と\(\small{ \ 2337 \ }\)の最大公約数を考えていこう。
とにかく「大きい数を小さい数で割って、その余りでさらに小さい数を割る」を繰り返せばいいから

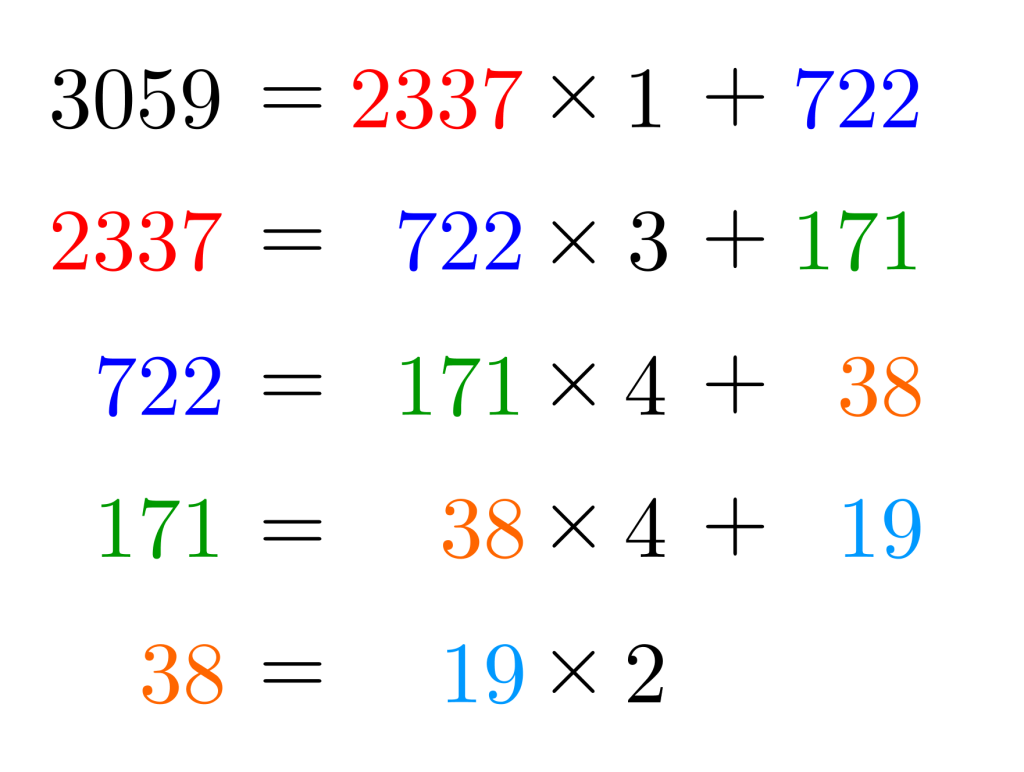
こうなるよね。
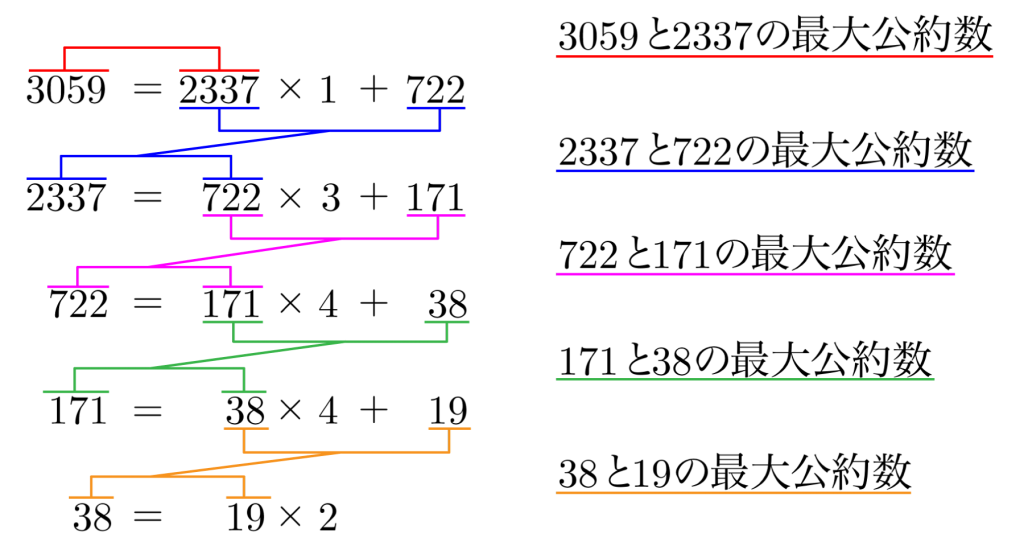
つまり最後に余りがなくなったその数が最大公約数ってことになるから、最大公約数は\(\small{ \ 19 \ }\)になるんだ。

つまり割り算をすることで、最大公約数を求める\(\small{ \ 2 \ }\)つの数を小さくしていくってことになるからね。

文字を含んだユークリッドの互除法

ユークリッドの互除法で最大公約数を求めることができるってことがわかったけど、次に\(\small{ \ n \ }\)を含む自然数の最大公約数について考えてみよう。

例えば\(\small{ \ 5n+40 \ }\)と\(\small{ \ 2n+19 \ }\)の最大公約数についてもユークリッドの互除法で考えることができるんだ。

といってもこの\(\small{ \ n \ }\)を含んだまま答えを出すっていうのじゃなくて、問題は「\(\small{ \ 5n+40 \ }\)と\(\small{ \ 2n+19 \ }\)の最大公約数が\(\small{ \ 5 \ }\)になるような\(\small{ \ 20 \ }\)以下の自然数\(\small{ \ n \ }\)を求めよ」のように\(\small{ \ n \ }\)に制限をつけた問題になってる。制限がないとめちゃくちゃあって大変だからね。

割り算を繰り返すと
\(\small{ \ 5n+40=2(2n+19)+n+2 \ }\)
\(\small{ \ 2n+19=2(n+2)+15 \ }\)
ってなって、ユークリッドの互除法から\(\small{ \ 5n+40 \ }\)と\(\small{ \ 2n+19 \ }\)の最大公約数は\(\small{ \ n+2 \ }\)と\(\small{ \ 15 \ }\)の最大公約数に等しいよね。

だから\(\small{ \ n+2 \ }\)と\(\small{ \ 15 \ }\)の最大公約数が\(\small{ \ 5 \ }\)になればいいから、\(\small{ \ n+2 \ }\)が\(\small{ \ 5 \ }\)の倍数で\(\small{ \ 3 \ }\)の倍数じゃないってこと。
つまりこれから\(\small{ \ n+2=5, \ 10, \ 20, \ 25, \ 35, \ 40,cdots \ }\)ってなって、\(\small{ \ n \ }\)は\(\small{ \ 20 \ }\)以下の自然数だから1\(\small{ \ n=3, \ 8, \ 18 \ }\)が求める値になるんだ。

ユークリッドの互除法は文字を含んだ式でも利用できるってことを覚えておこう。

文字を含む式を割り算していくと、この例題みたいに余りが負の数になることがあるけど、負の数の絶対値をとった正の数との最大公約数を求めよう。

Point ユークリッドの互除法と最大公約数

①最大公約数を求めるのは連除法かユークリッドの互除法
②ユークリッドの互除法は割れなくなるまで繰り返す