中国剰余定理

こんにちは、リンス(@Lins016)です。
今回は中国剰余定理について学習していこう。

中国剰余定理とは

中国の算術書「孫子算経」に「\(\small{ \ 3 \ }\)で割ると\(\small{ \ 2 \ }\)余り、\(\small{ \ 5 \ }\)で割ると\(\small{ \ 3 \ }\)余り、\(\small{ \ 7 \ }\)で割ると\(\small{ \ 2 \ }\)余る数は何か」という問題とその解法が書かれていた。

これを他の整数についても解けるように一般化したものが中国剰余定理と呼ばれるものなんだ。名前の由来はもちろん中国の算術書から。

この定理が高校数学ですごく有名ってことではなくて、この問題を合同式や\(\small{ \ 1 \ }\)次不定方程式を利用して考えてみようってことで今回は記事を書いてるからね。

だから中国剰余定理の証明については書いてない。記事の最後に他サイトのリンクを貼ってるから証明について知りたい人はそっちを確認してほしい。

だから今回は孫子算経に載っているその問題を考えてみよう。

この問題を解く前に

という問題とは違うことを認識しておこう。
これを満たす数を\(\small{ \ n \ }\)とすると\(\small{ \ n+2 \ }\)は\(\small{ \ 3 \ }\)でも\(\small{ \ 5 \ }\)でも\(\small{ \ 7 \ }\)でも割り切れるよね。この問題みたいにある数をたすと割り切れるっていう風にはならないからね。

合同式の利用

合同式を利用して解いてみよう。
まずは合同式について復習しておこう。

\(\small{\begin{eqnarray}
\left\{
\begin{array}{l}
x \equiv 2 \pmod 3\cdots① \\
x \equiv 3 \pmod 5\cdots②\\
x \equiv 2 \pmod 7\cdots③
\end{array}
\right.
\end{eqnarray}
\ }\)
\(\small{ \ ①}\)より\(\small{ \ x=3k_1+2 \ (k_1\in\mathbb{Z})\cdots④}\)
これを\(\small{ ②}\)に代入すると
\(\small{ \ 3k_1+2 \equiv 3 \pmod 5 \ }\)
\(\small{ \ 3k_1 \equiv 1 \pmod 5 \ }\)
\(\small{ \ 3k_1 \equiv 6 \pmod 5 \ }\)
\(\small{ \ k_1 \equiv 2 \pmod 5 \ }\)
\(\small{ \ \therefore k_1=5k_2+2 \ (k_2\in\mathbb{Z}) \ }\)
これを\(\small{④}\)に代入して
\(\small{\begin{eqnarray} \ x&=&3k_1+2\\
&=&15k_2+8\cdots⑤ \end{eqnarray}}\)
これを\(\small{③}\)すると
\(\small{ \ 15k_2+8 \equiv 2 \pmod 7 \ }\)
\(\small{ \ 15k_2 \equiv -6 \pmod 7 \ }\)
\(\small{ \ 15k_2 \equiv 1 \pmod 7 \ }\)
\(\small{ \ 15k_2 \equiv 15 \pmod 7 \ }\)
\(\small{ \ k_2 \equiv 1 \pmod 7 \ }\)
\(\small{ \ \therefore k_2=7k_3+1 \ (k_3\in\mathbb{Z}) \ }\)
これを\(\small{⑤}\)に代入して
\(\small{\begin{eqnarray} \ x&=&15k_2+8\\[3pt] &=&105k_3+23 \ \end{eqnarray}}\)
よって求める答えは
\(\small{ \ 105k+23 \ (k\in\mathbb{Z})}\)

一次不定方程式の利用

次に一次不定方程式を使って解いてみよう。
一次不定方程式については次の記事を確認しておこう。

\(\small{\begin{eqnarray}
\left\{
\begin{array}{l}
x=3k_1+2\cdots① \\
x=5k_2+3\cdots②\\
x=7k_3+2\cdots③
\end{array}
\right.
\end{eqnarray} \ }\)
とおく
ただし、\(\small{ \ k_i\in\mathbb{Z}, \ i=1, \ 2, \ 3, \ 4, \ 5, \ 6 \ }\)
\(\small{ \ 3k_1+2=5k_2+3 \ }\)
\(\small{ \ 3k_1-5k_2=1 \ }\)
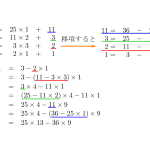
\(\small{ \ 5=3\cdot1+2 \ }\)
\(\small{ \ 3=2\cdot1+1 \ }\)より
\(\small{\begin{eqnarray} \ 1&=&3-2\cdot1\\[3pt] &=&3-(5-3\cdot1)\\[3pt] &=&3\cdot2-5\cdot1 \ \end{eqnarray}}\)
\(\small{\begin{eqnarray} \ &&3k_1&-&5k_2&=&1\\[3pt] &-)&3\cdot2&-&5\cdot1&=&1\\[3pt] \hline
&&3(k_1-2)&-&5(k_2-1)&=&0 \ \end{eqnarray}}\)
\(\small{ \ 3(k_1-2)=5(k_2-1) \ }\)
\(\small{\begin{eqnarray}
\left\{
\begin{array}{l}
k_1=5k_4+2\cdots④ \\
k_2=3k_4+1\cdots⑤
\end{array}
\right.
\end{eqnarray} \ }\)
\(\small{ \ ②, \ ③ \ }\)より
\(\small{ \ 3k_1+2=7k_3+2 \ }\)
\(\small{ \ ④}\)を代入し
\(\small{ \ 3(5k_4+2)+2=7k_3+2 \ }\)
\(\small{ \ 15k_4-7k_3=-6 \ }\)
\(\small{ \ 15=7\cdot2+1 \ }\)より
\(\small{ \ 1=15-7\cdot2 \ }\)
\(\small{\begin{eqnarray} \ &&15k_4&-&7k_3&=&-6\\[3pt] &-)&15\cdot(-6)&-&7\cdot(-12)&=&-6\\[3pt] \hline
&&15(k_4+6)&-&7(k_3+12)&=&0 \ \end{eqnarray}}\)
\(\small{ \ 15(k_4+6)=7(k_3+12) \ }\)
\(\small{\begin{eqnarray}
\left\{
\begin{array}{l}
k_4=7k_5-6\cdots⑥\\
k_3=15k_5-12\cdots⑦
\end{array}
\right.
\end{eqnarray} \ }\)
\(\small{ \ ④, \ ⑥ \ }\)より
\(\small{\begin{eqnarray} \ k_1=5(7k_5-6)+2\\
=35k_5-28 \ \end{eqnarray}}\)
\(\small{ \ ① \ }\)より
\(\small{\begin{eqnarray} \ x&=&3(35k_5-28)+2\\
&=&105k_5-82\\
&=&105k_6+23 \ \end{eqnarray}}\)
よって求める答えは
\(\small{ \ 105k+23 \ (k\in\mathbb{Z})}\)

項の和を利用

次はあらかじめそれぞれの割った余りの項を作ってそれを足す方法を考えてみよう。
\(\small{ \ 5\times7\times a \ }\)を\(\small{ \ 3 \ }\)で割ると\(\small{ \ 2 \ }\)余る
\(\small{ \ 3\times7\times b \ }\)を\(\small{ \ 5 \ }\)で割ると\(\small{ \ 3 \ }\)余る
\(\small{ \ 3\times5\times c \ }\)を\(\small{ \ 7 \ }\)で割ると\(\small{ \ 2 \ }\)余る
これらを満たす数をそれぞれ求めると
\(\small{ \ a=1, \ b=3, \ c=2 \ }\)

\(\small{ \ 3\times7\times b \ }\)を\(\small{ \ 5 \ }\)で割った余りを考えるとき、\(\small{ \ 3\times7 \ }\)を\(\small{ \ 5 \ }\)で割った余りは\(\small{ \ 1 \ }\)だから、これを\(\small{ \ b \ }\)倍したとき割った余りは\(\small{ \ b \ }\)を割った余りと同じになるよね。だから\(\small{ \ 5 \ }\)で割った余りが\(\small{ \ 3 \ }\)になるのは\(\small{ \ b=3 \ }\)なんだ。

この\(\small{ \ 3 \ }\)つを足すと

これは\(\small{ \ 3 \ }\)で割ると\(\small{ \ 2 \ }\)余り、\(\small{ \ 5 \ }\)で割ると\(\small{ \ 3 \ }\)余り、\(\small{ \ 7 \ }\)で割ると\(\small{ \ 2 \ }\)余る数になるよね。
だってこの数は後ろに\(\small{ \ 2 \ }\)つの項は\(\small{ \ 3 \ }\)で割り切れるから、\(\small{ \ 3 \ }\)で割った余りは最初の項を\(\small{ \ 3 \ }\)で割った余りと同じになるよね。\(\small{ \ 5 \ }\)で割ったとき、\(\small{ \ 7 \ }\)で割ったときも同じように言えるよね。

これを満たす数は\(\small{ \ 3\times5\times7=105 \ }\)を\(\small{ \ 1 \ }\)周期として繰り返すから、\(\small{ \ k, \ l \ }\)を用いて（\(\small{ \ k\in\mathbb{Z}, \ l\in\mathbb{Z} \ }\)）
\(\small{ \ 105k+128=105l+23 \ }\)とかけるんだ。

ただ、「\(\small{ \ 3\times5\times7=105 \ }\)を\(\small{ \ 1 \ }\)周期として繰り返す」とき、「\(\small{ \ 3 \ }\)で割ると\(\small{ \ 2 \ }\)余り、\(\small{ \ 5 \ }\)で割ると\(\small{ \ 3 \ }\)余り、\(\small{ \ 7 \ }\)で割ると\(\small{ \ 2 \ }\)余る数」が\(\small{ \ 1 \ }\)周期に\(\small{ \ 1 \ }\)つしかないことを言わないといけない。

\(\small{ \ 3 \ }\)で割った余りは\(\small{ \ 0, \ 1, \ 2 \ }\)の\(\small{ \ 3 \ }\)通り。
\(\small{ \ 5 \ }\)で割った余りは\(\small{ \ 0, \ 1, \ 2, \ 3, \ 4}\)の\(\small{ \ 5 \ }\)通り
\(\small{ \ 7 \ }\)で割った余りは\(\small{ \ 0, \ 1, \ 2, \ 3, \ 4, \ 5, \ 6}\)の\(\small{ \ 7 \ }\)通り
だから余りの組み合わせは\(\small{ \ 3\times5\times7=105 \ }\)通りになる。
だから\(\small{ \ 1 \ }\)周期に「\(\small{ \ 3 \ }\)で割ると\(\small{ \ 2 \ }\)余り、\(\small{ \ 5 \ }\)で割ると\(\small{ \ 3 \ }\)余り、\(\small{ \ 7 \ }\)で割ると\(\small{ \ 2 \ }\)余る数」は\(\small{ \ 1 \ }\)つしか存在しない。

ちなみに\(\small{ \ 3 \ }\)で割ると\(\small{ \ 2 \ }\)余り、\(\small{ \ 5 \ }\)で割ると\(\small{ \ 3 \ }\)余り、\(\small{ \ 7 \ }\)で割ると\(\small{ \ 2 \ }\)余る数が\(\small{ \ 1〜105 \ }\)の中に\(\small{ \ 2 \ }\)つあるとして、その数を\(\small{ \ P, \ Q \ }\)としてみよう。\(\small{ \ P-Q \ }\)は\(\small{ \ 3 \ }\)でも\(\small{ \ 5 \ }\)でも\(\small{ \ 7 \ }\)でも割り切れるよね。
だから\(\small{ \ P-Q \ }\)は\(\small{ \ 3 \ }\)の倍数でもあるし、\(\small{ \ 5 \ }\)の倍数でもあるし、\(\small{ \ 7 \ }\)の倍数でもあるから、\(\small{ \ 105 \ }\)の倍数ってことになる。

でも\(\small{ \ P, \ Q \ }\)はどちらも\(\small{ \ 105 \ }\)以下の数だから矛盾する。だから\(\small{ \ 2 \ }\)つは存在しないことも言えるよね。

おまけ

ちなみに孫子算経の本文はこれ。

ちなみに和算では未知の数を\(\small{ \ 3, \ 5, \ 7 \ }\)でそれぞれ割った余りから元の数を求める計算を\(\small{ \ 3\times5\times7=105 \ }\)から百五減算って読んでる。

中国剰余定理についてもっと詳しく知りたい人は次のページとか見てみるといいかも

Point 中国剰余定理

①余りの問題は合同式や一次方程式を利用する