こんにちは、リンス(@Lins016)です。
今回は複素数平面上での回転移動の応用について学習していこう。
回転移動とその応用
複素数平面上の点\(\small{ \ \mathrm{P}(z) \ }\)に\(\small{ \ \cos \theta+i\sin \theta \ }\)をかけると、原点を中心として\(\small{ \ \theta \ }\)回転するんだったよね。
このことを忘れているなら、まずは次の記事を確認しておこう。今回の内容はこの応用になるからね。
-

複素数の極形式と乗法・除法
極形式への変形や複素数の乗法・除法による複素数平面上での移動について詳しく解説しています。
続きを見る
回転移動をさらに応用していろいろな問題を考えてみよう。
・原点以外の点まわりの回転移動
点\(\small{ \ \mathrm{Q}(\beta) \ }\)を点\(\small{ \ \mathrm{P}(\alpha) \ }\)まわりに\(\small{ \ \theta \ }\)回転させた点\(\small{ \ \mathrm{R}(\gamma) \ }\)とする
\(\small{ \ \displaystyle\frac{\gamma-\alpha}{\beta-\alpha}=\cos \theta+i\sin \theta \ }\)
特に\(\small{ \ \mathrm{P, \ Q, \ R} \ }\)が同一直線上の場合
\(\small{ \ \displaystyle\frac{\gamma-\alpha}{\beta-\alpha}=\overline{\displaystyle\frac{\gamma-\alpha}{\beta-\alpha}} \ }\)
・直線OAに関する対称移動
原点\(\small{ \ \mathrm{O} \ }\)と点\(\small{ \ \mathrm{A}(\alpha) \ }\)を結んだ直線に関して点\(\small{ \ \mathrm{P}(z) \ }\)を対称移動した点を\(\small{ \ \mathrm{Q}(\omega) \ }\)とするとき
\(\small{ \ \omega=\alpha\overline{\left(\displaystyle\frac{z}{\alpha}\right)}=\displaystyle\frac{\alpha}{\overline{\alpha}}\overline{z}=\alpha^2z \ }\)
ただし\(\small{ \ |\alpha|=1 \ }\)
原点以外の点まわりの回転移動
点\(\small{ \ \mathrm{Q}(\beta) \ }\)を点\(\small{ \ \mathrm{P}(\alpha) \ }\)まわりに\(\small{ \ \theta \ }\)回転した点\(\small{ \ \mathrm{R}(\gamma) \ }\)について考えてみよう。
回転については前に学習したように\(\small{ \ \cos\theta+i\sin\theta \ }\)をかけたら原点まわりに\(\small{ \ \theta \ }\)回転できるんだったよね。原点以外の点のまわりの回転についても、やっぱりこれを利用したいんだ。
だから平行移動して考えよう。点\(\small{ \ \mathrm{P}(\alpha) \ }\)を原点に移動しよう。それと同じように点\(\small{ \ \mathrm{Q}(\beta) \ }\)と点\(\small{ \ \mathrm{R}(\gamma) \ }\)も平行移動する。
この移動した点を\(\small{ \ \mathrm{Q', \ R'} \ }\)とすると\(\small{ \ \mathrm{Q'}(\beta-\alpha) \ }\)、\(\small{ \ \mathrm{R'}(\gamma-\alpha) \ }\)になるよね。まずはこの\(\small{ \ \mathrm{Q'} \ }\)を原点まわりに\(\small{ \ \theta \ }\)回転させよう。
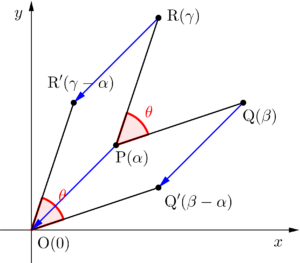
\(\small{ \ \mathrm{Q'} \ }\)を原点まわりに\(\small{ \ \theta \ }\)回転させた点が\(\small{ \ \mathrm{R'} \ }\)になるから、\(\small{ \ \gamma-\alpha=(\beta-\alpha)(\cos\theta+i\sin\theta) \ }\)になるよね。
つまり点\(\small{ \ \mathrm{R}(\gamma) \ }\)はこの式を整理して、\(\small{ \ \gamma=(\beta-\alpha)(\cos\theta+i\sin\theta)+\alpha \ }\)になるんだ。
これって\(\small{ \ \mathrm{R'} \ }\)を\(\small{ \ \mathrm{R} \ }\)に平行移動した式ってみることができるよね。
参考書とかだと\(\small{ \ \displaystyle\frac{\gamma-\alpha}{\beta-\alpha}=\cos\theta+i\sin\theta \ }\)って書いてあることが多いけど、回転した点\(\small{ \ \mathrm{R}(\gamma) \ }\)を求めるなら、\(\small{ \ \gamma=(\beta-\alpha)(\cos\theta+i\sin\theta)+\alpha \ }\)まで変形しないといけないからね。
ちなみにこれは単純に回転させた式だったけど、回転して拡大(縮小)するなら \(\small{ \ \gamma=(\beta-\alpha)\times r(\cos\theta+i\sin\theta)+\alpha \ }\)って回転を表す複素数\(\small{ \ \cos\theta+i\sin\theta \ }\)を\(\small{ \ r \ }\)倍すればいいからね。
\(\small{ \ \alpha=2-\sqrt{3}i, \ \beta=4+\sqrt{3}i \ }\)について、点\(\small{ \ \beta \ }\)を点\(\small{ \ \alpha \ }\)の周りに\(\small{ \ \displaystyle\frac{\pi}{3} \ }\)回転した点を表す複素数を求めよ。
\(\small{ \ \beta-\alpha=2+2\sqrt{3}i \ }\)
\(\small{ \ (2+2\sqrt{3}i)\left(\cos \displaystyle\frac{\pi}{3}+i\sin \displaystyle\frac{\pi}{3}\right)\\[3pt]
=\displaystyle\frac{1}{2}(2+2\sqrt{3}i)(1+\sqrt{3}i)\\[3pt]
=\displaystyle\frac{1}{2}(-4+4\sqrt{3}i)\\[3pt]
=-2+2\sqrt{3}i \ }\)
よって求める答えは
\(\small{ \ -2+2\sqrt{3}i+2-\sqrt{3}i =\sqrt{3}i \ }\)
同一直線上の複素数
三点\(\small{ \ \mathrm{P}(\alpha), \ \mathrm{Q}(\beta), \ \mathrm{R}(\gamma) \ }\)が同一直線上にある条件について考えてみよう。
同一直線上にあるっていうのは回転の応用でみると点\(\small{ \ \mathrm{Q}(\beta) \ }\)を点\(\small{ \ \mathrm{P}(\alpha) \ }\)まわりに\(\small{ \ 180^{\circ} \ }\)または\(\small{ \ 360^{\circ} \ }\)回転した点\(\small{ \ \mathrm{R}(\gamma) \ }\)ってみることができるよね。(もちろん\(\small{ \ 360^{\circ} \ }\)じゃなくて\(\small{ \ 0^{\circ} \ }\)でもいいよね)。
当然\(\small{ \ 360^{\circ} \ }\)以上回転してもいいから「\(\small{ \ 180^{\circ} \times \ }\)整数」回転させることで同一直線上を表すことができる。

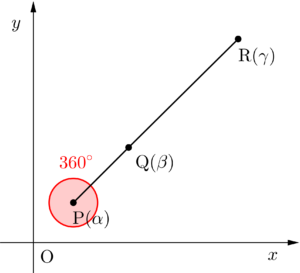
このとき回転する角は弧度法を使って\(\small{ \ \theta=n\pi \ }\)(\(\small{ \ n \ }\)は整数)になるから
ってことになるよね。
つまり\(\small{ \ r(\cos\theta+i\sin\theta) \ }\)は実数になるんだ。
ちなみに複素数\(\small{ \ z \ }\)が実数のとき\(\small{ \ z=\bar{z} \ }\)が成り立つんだったよね。
だから\(\small{ \ \mathrm{P}(\alpha) \ }\)、\(\small{ \ \mathrm{Q}(\beta) \ }\)、\(\small{ \ \mathrm{R}(\gamma) \ }\)が同一直線上にあるとき
\(\small{ \ \displaystyle\frac{\gamma-\alpha}{\beta-\alpha}=\overline{\displaystyle\frac{\gamma-\alpha}{\beta-\alpha}} \ }\)が成り立つんだ。
\(\small{ \ \mathrm{A}(5-4i) \ }\)、\(\small{ \ \mathrm{B}(3-2i) \ }\)、\(\small{ \ \mathrm{C}(x-i) \ }\)が一直線上にあるとき、実数\(\small{ \ x \ }\)の値を求めよ。
\(\small{ \ \displaystyle\frac{(x-i)-(5-4i)}{(3-2i)-(5-4i)} \ }\)
\(\small{ \ =\displaystyle\frac{x-5+3i}{-2+2i} \ }\)
\(\small{ \ =\displaystyle\frac{(x-5+3i)(-2-2i)}{(-2+2i)(-2-2i)} \ }\)
\(\small{ \ =\displaystyle\frac{(-2x+6)+(-2x+4)i}{8} \ }\)
\(\small{ \ =\displaystyle\frac{(-x+3)+(-x+2)i}{4} \ }\)
三点が一直線上にあるとき、これが実数になるので
\(\small{ \ -x+2=0 \ }\)
\(\small{ \ \therefore x=2 \ }\)
複素数平面を座標平面にして考えると
\(\small{ \ \mathrm{A}(5, \ -4) \ }\)、\(\small{ \ \mathrm{B}(3, \ -2) \ }\)、\(\small{ \ \mathrm{C}(x, \ -1) \ }\)
三点が一直線上にあるとき、この直線の傾きは等しいので
\(\small{ \ \displaystyle\frac{-1-(-4)}{x-5}=\displaystyle\frac{-2-(-4)}{3-5} \ }\)
\(\small{ \ \displaystyle\frac{3}{x-5}=-1 \ }\)
\(\small{ \ x-5=-3 \ }\)
\(\small{ \ \therefore x=2 \ }\)

複素数平面は『横軸が実軸、縦軸が虚軸で複素数\(\small{ \ z=a+bi \ }\)を座標で表すことができる平面』のこと。
これに対して、図形と方程式や、二次関数等で使う\(\small{ \ xy \ }\)平面(座標平面)は実数\(\small{ \ (x, \ y) \ }\)を座標で表したもので、複素数は出てこないからね。
ただ、複素数\(\small{ \ a+bi \ }\)を座標平面\(\small{ \ (a, \ b) \ }\)に対応させたものが複素数平面ってことだから、ほとんど同じに見えるけどね。
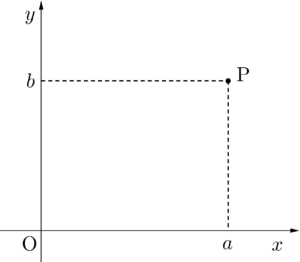
平面上に\(\small{ \ \mathrm{P}(a, \ b) \ }\)って書いてれば座標平面、\(\small{ \ \mathrm{P}(a+bi) \ }\)って書いてれば複素数平面ってことになるよね。
直線に関しての対称移動
原点\(\small{ \ \mathrm{O} \ }\)と点\(\small{ \ \mathrm{A} \ }\)と点\(\small{ \ \mathrm{P} \ }\)があるとき、直線\(\small{ \ \mathrm{OA} \ }\)に関して点\(\small{ \ \mathrm{P} \ }\)を対称移動した点\(\small{ \ \mathrm{Q} \ }\)について考えてみよう。
\(\small{ \ \mathrm{A} \ }\)を表す複素数が\(\small{ \ r(\cos \theta+i\sin \theta) \ }\)だとすると、まずはすべての点を原点を中心に\(\small{ \ -\theta \ }\)回転させよう。
この回転を考えるとき、\(\small{ \ \mathrm{A} \ }\)を表す複素数をそのまま使うと、\(\small{ \ r \ }\)が入って単純な回転にならない(\(\small{ \ r \ }\)倍拡大または縮小される)から、今回は図形的にわかりやすいように\(\small{ \ \mathrm{OA} \ }\)上にある大きさ\(\small{ \ 1 \ }\)の複素数\(\small{ \ \alpha \ }\)を別にとって\(\small{ \ \alpha=\cos \theta+i\sin \theta \ }\)として回転を考えよう。
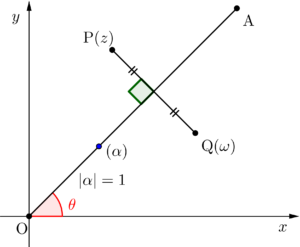
点\(\small{ \ \mathrm{P}(z) \ }\)を\(\small{ \ -\theta \ }\)回転移動させた点を\(\small{ \ \mathrm{P'} \ }\)とすると点\(\small{ \ \mathrm{P'}\left(\displaystyle\frac{z}{\alpha}\right) \ }\)になる。
これを\(\small{ \ x \ }\)軸に対称移動させた\(\small{ \ \mathrm{Q'} \ }\)は点\(\small{ \ \mathrm{P'}\left(\displaystyle\frac{z}{\alpha}\right) \ }\)の共役だから\(\small{ \ \mathrm{Q'}\overline{\left(\displaystyle\frac{z}{\alpha}\right)} \ }\)になるよね。
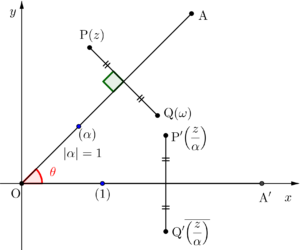
後はこれをもう一度\(\small{ \ \theta \ }\)回転移動させれば点\(\small{ \ \mathrm{Q} \ }\)になるんだ。
点\(\small{ \ \mathrm{Q} \ }\)を表す複素数を\(\small{ \ \omega \ }\)とすると\(\small{ \ \omega=\overline{\left(\displaystyle\frac{z}{\alpha}\right)}\alpha \ }\)になる。
これを式変形すると
\(\small{\begin{eqnarray} \ \omega&=&\overline{\left(\displaystyle\frac{z}{\alpha}\right)}\alpha\\[3pt]
&=&\displaystyle\frac{\alpha}{\bar{\alpha}}\bar{z} \ \end{eqnarray}}\)
ここで\(\small{ \ \mathrm{arg} \ \bar{\alpha}=-\theta \ }\)かつ\(\small{ \ \left|\bar{\alpha}\right|=1 \ }\)だから\(\small{ \ \displaystyle\frac{\alpha}{\bar{\alpha}} \ }\)は\(\small{ \ \alpha \ }\)を原点を中心に\(\small{ \ -\theta \ }\)逆に回転する、つまり原点を中心に\(\small{ \ \theta \ }\)回転することになる。
さらに\(\small{ \ \mathrm{arg} \ \alpha=\theta \ }\)より\(\small{ \ \displaystyle\frac{\alpha}{\bar{\alpha}}=\cos 2\theta+i\sin2\theta \ }\)になるんだ。だから\(\small{ \ \displaystyle\frac{\alpha}{\bar{\alpha}}\bar{z} \ }\)は点\(\small{ \ \mathrm{R}(\bar{z}) \ }\)を原点まわりに\(\small{ \ 2\theta \ }\)回転させた点になるんだ。
確かに図形的に見てもそうなってそうだよね。
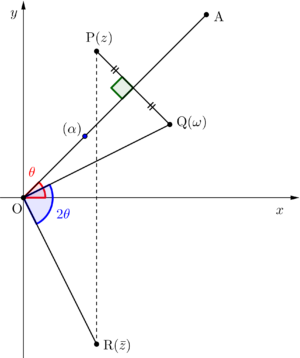

\(\small{ \ \mathrm{A}(z_\mathrm{A}) \ }\)の複素数を\(\small{ \ z_\mathrm{A}=r(\cos\theta+i\sin \theta) \ }\)として上の式をそのまま使うと
つまり\(\small{ \ \bar{z} \ }\)を\(\small{ \ 2\theta \ }\)回転させた点を表すってことがわかるよね。
ちなみに\(\small{ \ |\alpha|=1 \ }\)なら\(\small{ \ \alpha\bar{\alpha}=1 \ }\)を使って
\(\small{\begin{eqnarray} \ \omega&=&\overline{\left(\displaystyle\frac{z}{\alpha}\right)}\alpha\\[3pt]
&=&\displaystyle\frac{\alpha}{\bar{\alpha}}\bar{z}\\[3pt]
&=&\alpha^2z \ \end{eqnarray}}\)
まで変形できるんだ。
Point 複素数平面上での回転移動の応用
①原点以外の点まわりの回転移動の式\(\small{ \ \displaystyle\frac{\gamma-\alpha}{\beta-\alpha}=\cos\theta+i\sin\theta \ }\)を覚える
②三点が同一直線上は回転の式が実数になる\(\small{ \ \displaystyle\frac{\gamma-\alpha}{\beta-\alpha}=\overline{\displaystyle\frac{\gamma-\alpha}{\beta-\alpha}} \ }\)
③線対称の移動の式\(\small{ \ \omega=\overline{\left(\displaystyle\frac{z}{\alpha}\right)}\alpha \ }\)を覚える
複素数平面上で原点\(\small{ \ \mathrm{O} \ }\)と二点\(\small{ \ \mathrm{A}(\alpha), \ \mathrm{B}(\beta) \ }\)を頂点とする\(\small{ \ \triangle \mathrm{OAB} \ }\)がある。直線\(\small{ \ \mathrm{OB} \ }\)に関して点\(\small{ \ \mathrm{A} \ }\)と対称な点\(\small{ \ \mathrm{C} \ }\)、直線\(\small{ \ \mathrm{OA} \ }\) に関して点\(\small{ \ \mathrm{B} \ }\)と対称な点を\(\small{ \ \mathrm{D} \ }\)とするとき、次の問いに答えよ。
(1)点\(\small{ \ \mathrm{C}(\gamma) \ }\)とするとき、\(\small{ \ \gamma=\overline{\left(\displaystyle\frac{\alpha}{\beta}\right)}\beta \ }\)であることを示せ。
(2)辺\(\small{ \ \mathrm{AB} \ }\)と直線\(\small{ \ \mathrm{DC} \ }\)が平行なとき、\(\small{ \ \triangle \mathrm{OAB} \ }\)はどのような三角形か。
\(\small{ \ \mathrm{O}, \ \mathrm{A}(\alpha), \ \mathrm{B}(\beta) \ }\)は三角形の頂点だから
\(\small{ \ \alpha\neq0, \ \beta\neq0, \ \alpha\neq\beta \ }\)
\(\small{ \ \mathrm{arg} \ \displaystyle\frac{\beta}{\alpha}=\mathrm{arg} \ \displaystyle\frac{\gamma}{\beta}=\theta \ }\)とおくと
\(\small{ \ \gamma=\displaystyle\frac{|\gamma|}{|\beta|}(\cos \theta+i\sin \theta)\beta\cdots① \ }\)
また\(\small{ \ \mathrm{arg} \ \displaystyle\frac{\alpha}{\beta}=-\theta \ }\)だから
\(\small{\begin{eqnarray} \ \displaystyle\frac{\alpha}{\beta}&=&\displaystyle\frac{|\alpha|}{|\beta|}\left\{\cos \left(-\theta\right)+i\sin \left(-\theta\right)\right\}\\[3pt]
&=&\displaystyle\frac{|\alpha|}{|\beta|}\left(\cos\theta-i\sin\theta\right) \ \end{eqnarray}}\)
\(\small{ \ \therefore \overline{\left(\displaystyle\frac{\alpha}{\beta}\right)}=\displaystyle\frac{|\alpha|}{|\beta|}\left(\cos\theta+i\sin\theta\right) \ }\)
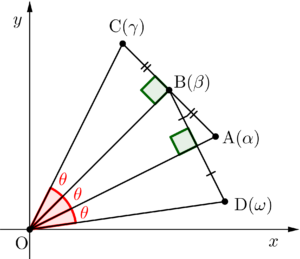
これと\(\small{ \ ①}\)より
\(\small{\begin{eqnarray} \ \gamma&=&\displaystyle\frac{|\gamma|}{|\beta|}\cdot\displaystyle\frac{|\beta|}{|\alpha|}\overline{\left(\displaystyle\frac{\alpha}{\beta}\right)}\beta\\[3pt]
&=&\displaystyle\frac{|\gamma|}{|\alpha|}\overline{\left(\displaystyle\frac{\alpha}{\beta}\right)}\beta \ \end{eqnarray}}\)
\(\small{ \ \mathrm{OA=OC} \ }\)より\(\small{ \ |\alpha|=|\gamma| \ }\)
よって\(\small{ \ \gamma=\overline{\left(\displaystyle\frac{\alpha}{\beta}\right)}\beta \ }\)
(2)点\(\small{ \ \mathrm{D}(\omega) \ }\)とすると、\(\small{ \ \mathrm{arg} \ \displaystyle\frac{\omega}{\alpha}=-\theta \ }\)
\(\small{\begin{eqnarray} \ \omega&=&\displaystyle\frac{|\omega|}{|\alpha|}\left\{\cos \left(-\theta\right)+i\sin \left(-\theta\right)\right\}\alpha\\[3pt]
&=&\displaystyle\frac{|\omega|}{|\alpha|}\left(\cos \theta-i\sin\theta\right)\alpha \ \end{eqnarray}}\)
また
\(\small{ \ \displaystyle\frac{\beta}{\alpha}=\displaystyle\frac{|\beta|}{|\alpha|}(\cos \theta+i\sin\theta) \ }\)より
\(\small{ \ \overline{\left(\displaystyle\frac{\beta}{\alpha}\right)}=\displaystyle\frac{|\beta|}{|\alpha|}(\cos \theta-i\sin\theta) \ }\)
よって
\(\small{\begin{eqnarray} \ \omega&=&\displaystyle\frac{|\omega|}{|\alpha|}\cdot\displaystyle\frac{|\alpha|}{|\beta|}\overline{\left(\displaystyle\frac{\beta}{\alpha}\right)}\alpha \\[3pt]
&=&\displaystyle\frac{|\omega|}{|\beta|}\overline{\left(\displaystyle\frac{\beta}{\alpha}\right)}\alpha \ \end{eqnarray}}\)
\(\small{ \ \mathrm{OB=OD} \ }\)より\(\small{ \ |\beta|=|\omega| \ }\)より
\(\small{ \ \omega=\overline{\left(\displaystyle\frac{\beta}{\alpha}\right)}\alpha \ }\)
辺\(\small{ \ \mathrm{AB} \ }\)と直線\(\small{ \ \mathrm{DC} \ }\)が平行なとき、\(\small{ \ \displaystyle\frac{\gamma-\omega}{\beta-\alpha} \ }\)は実数であるから
\(\small{ \ \displaystyle\frac{\gamma-\omega}{\beta-\alpha}=\overline{\displaystyle\frac{\gamma-\omega}{\beta-\alpha}} \ }\)
\(\small{ \ \displaystyle\frac{\gamma-\omega}{\beta-\alpha}=\displaystyle\frac{\bar{\gamma}-\bar{\omega}}{\bar{\beta}-\bar{\alpha}} \ }\)
\(\small{ \ \left\{\overline{\left(\displaystyle\frac{\alpha}{\beta}\right)}\beta-\overline{\left(\displaystyle\frac{\beta}{\alpha}\right)}\alpha\right\}\left(\bar{\beta}-\bar{\alpha}\right)= \left\{\left(\displaystyle\frac{\alpha}{\beta}\right)\bar{\beta}-\left(\displaystyle\frac{\beta}{\alpha}\right)\bar{\alpha}\right\}\left(\beta-\alpha\right) \ }\)
これを展開して整理すると
\(\small{ \ \left\{\displaystyle\frac{\beta}{\alpha}-\overline{\left(\displaystyle\frac{\alpha}{\beta}\right)}\right\}\bar{\alpha}\beta+\left\{\displaystyle\frac{\alpha}{\beta}-\overline{\left(\displaystyle\frac{\beta}{\alpha}\right)}\right\}\alpha\bar{\beta}=0 \ }\)
\(\small{ \ \displaystyle\frac{|\beta|^2-|\alpha|^2}{\alpha\bar{\beta}}\bar{\alpha}\beta+\displaystyle\frac{|\alpha|^2-|\beta|^2}{\bar{\alpha}\beta}\alpha\bar{\beta}=0 \ }\)
\(\small{ \ \left(|\beta|^2-|\alpha|^2\right)\left(\displaystyle\frac{\bar{\alpha}\beta}{\alpha\bar{\beta}}-\displaystyle\frac{\alpha\bar{\beta}}{\bar{\alpha}\beta}\right)=0 \ }\)
よって\(\small{ \ |\alpha|^2=|\beta|^2 \ }\)または\(\small{ \ \displaystyle\frac{\bar{\alpha}\beta}{\alpha\bar{\beta}}=\displaystyle\frac{\alpha\bar{\beta}}{\bar{\alpha}\beta} \ }\)
(i)\(\small{ \ |\alpha|^2=|\beta|^2 \ }\)のとき
\(\small{ \ \mathrm{OA}=\mathrm{OB} \ }\)
よって\(\small{ \ \mathrm{OA}=\mathrm{OB} \ }\)の二等辺三角形
(ii)\(\small{ \ \displaystyle\frac{\bar{\alpha}\beta}{\alpha\bar{\beta}}=\displaystyle\frac{\alpha\bar{\beta}}{\bar{\alpha}\beta} \ }\)のとき
\(\small{ \ \left(\displaystyle\frac{\beta}{\alpha}\right)^2=\left\{\overline{\left(\displaystyle\frac{\beta}{\alpha}\right)}\right\}^2 \ }\)より
\(\small{ \ \displaystyle\frac{\beta}{\alpha}=\overline{\left(\displaystyle\frac{\beta}{\alpha}\right)} \ }\)または\(\small{ \ \displaystyle\frac{\beta}{\alpha}=-\overline{\left(\displaystyle\frac{\beta}{\alpha}\right)} \ }\)
よって\(\small{ \ \displaystyle\frac{\beta}{\alpha} \ }\)は実数または純虚数である
\(\small{ \ \displaystyle\frac{\beta}{\alpha} \ }\)が実数のとき、三点\(\small{ \ \mathrm{O, \ A, \ B} \ }\)は同一直線上にあるため不適
\(\small{ \ \displaystyle\frac{\beta}{\alpha} \ }\)が純虚数のとき、\(\small{ \ \mathrm{OA} \ }\)と\(\small{ \ \mathrm{OB} \ }\)は直交する
よって\(\small{ \ \angle \mathrm{AOB}=90^{\circ} \ }\)の直角三角形
(i)(ii)より\(\small{ \ \triangle \mathrm{OAB} \ }\)は\(\small{ \ \mathrm{OA}=\mathrm{OB} \ }\)の二等辺三角形か\(\small{ \ \angle \mathrm{AOB}=90^{\circ} \ }\)の直角三角形である


