点の移動

こんにちは、リンス(@Lins016)です。
今回は点の移動について学習していこう。

点の移動

高校数学では座標で考えることって、とても多い。
「図形と方程式」や「ベクトル」「複素数平面」だってそうだよね。

もっと考えると、いろんな関数や微分積分だって\(\small{ \ xy \ }\)平面にグラフを書き込んだりするよね。
今回はそんな\(\small{ \ xy \ }\)平面上での点の移動について考えてみよう。

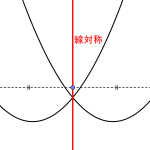
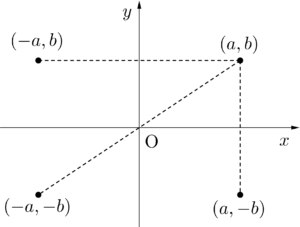
x軸・y軸・原点対称移動

\(\small{ \ x \ }\)軸に関して対称、\(\small{ \ y \ }\)軸に関して対称、原点に関して対称っていうのは図を見れば明らかだよね。

つまり座標の符号が反転するってことになる。

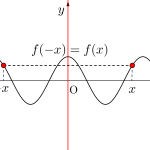
これはあくまで点の移動だけど、関数の表すグラフの曲線も点の集まりだから、あるグラフ上の点を対称移動させることを考えれば、そのグラフを対称移動させることになるよね。

だから\(\small{ \ y=f(x) \ }\)のグラフを\(\small{ \ y=f(-x) \ }\)にすれば\(\small{ \ y \ }\)軸に関して対称なグラフになるし、\(\small{ \ -y=f(x) \ }\)にすれば\(\small{ \ x \ }\)軸に関して対称なグラフになるんだ。

この軸に対称なグラフは、二次関数の定期試験に出題されるよね。

さらに深く考えると、\(\small{ \ y \ }\)軸対称の偶関数や原点対称の奇関数ってことにもつながっていくよね。

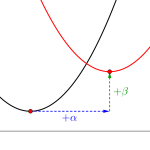
平行移動

\(\small{ \ (a, \ b) \ }\)を\(\small{ \ x \ }\)軸方向に\(\small{ \ +\alpha \ }\)、\(\small{ \ y \ }\)軸方向に\(\small{ \ +\beta \ }\)平行移動させると\(\small{ \ (a+\alpha, \ b+\beta) \ }\)になる。

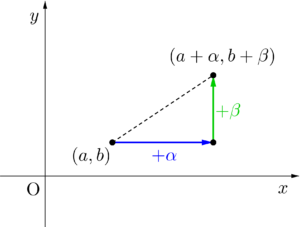
点だけならこれで終わりだけど、これを関数まで発展させてみよう。

移動した点を\(\small{ \ (x, \ y) \ }\)とすると
\(\small{ \begin{eqnarray}
\left\{
\begin{array}{l}
x=a+\alpha \\
y=b+\beta
\end{array}
\right.
\end{eqnarray}
\ }\)
これを変形すると
\(\small{ \begin{eqnarray}
\left\{
\begin{array}{l}
a=x-\alpha \\
b=y-\beta
\end{array}
\right.
\end{eqnarray}
\cdots① \ }\)
になる。

\(\small{ \ y=f(x) \ }\)上に\(\small{ \ (a, \ b) \ }\)があるとすると\(\small{ \ b=f(a) \ }\)
これに\(\small{ \ ①}\)を代入すると
\(\small{ \ y-\beta=f(x-\alpha) \ }\)

この式が\(\small{ \ y=f(x) \ }\) を\(\small{ \ x \ }\)軸方向に\(\small{ \ +\alpha \ }\)、\(\small{ \ y \ }\)軸方向に\(\small{ \ +\beta \ }\)平行移動した式になるんだ。

これは二次関数をはじめ、三角関数や指数関数でもよく使われる式だよね。

y=xに関して対称移動

\(\small{ \ (a, \ b) \ }\)と\(\small{ \ (p, \ q) \ }\)が\(\small{ \ y=x \ }\)に関して対称なら、二点を結ぶ線分と\(\small{ \ y=x \ }\)は垂直に交わるし、二点の中点は\(\small{ \ y=x \ }\)上にあるから
\(\small{ \begin{eqnarray}
\left\{
\begin{array}{l}
\displaystyle\frac{b-q}{a-p}\cdot1=-1\\
\displaystyle\frac{b+q}{2}=\displaystyle\frac{a+p}{2}
\end{array}
\right.
\end{eqnarray}\ }\)

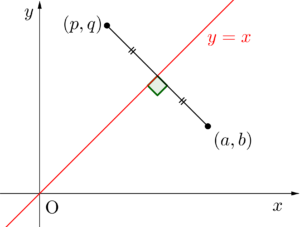
これを式変形すると
\(\small{ \begin{eqnarray}
\left\{
\begin{array}{l}
p+q=a+b \\
p-q=-a+b
\end{array}
\right.
\end{eqnarray} \ }\)
これを解いて、\(\small{ \ (p, \ q)=(b, a ) \ }\)になる。

つまり\(\small{ \ x \ }\)座標と\(\small{ \ y \ }\)座標を入れ替えたら\(\small{ \ y=x \ }\)に関して対称移動するんだ。

これを関数に発展させると\(\small{ \ y=f(x) \ }\)を\(\small{ \ y=x \ }\)に関して対称移動した関数は\(\small{ \ x=f(y) \ }\)になるんだ。

数学Ⅲまで勉強している人はあわせて逆関数のことまで思い出してほしいな。

数学Ⅱなら\(\small{ \ y=2^x \ }\)と\(\small{ \ y=\log_2x \ }\)が\(\small{ \ y=x \ }\)に対称だよね。

y=-xに関して対称移動

\(\small{ \ y=x \ }\)に関して対称移動と同じように\(\small{ \ (a, \ b) \ }\)と\(\small{ \ (p, \ q) \ }\)が\(\small{ \ y=-x \ }\)に関して対称なら、二点を結ぶ線分と\(\small{ \ y=-x \ }\)は垂直に交わるし、二点の中点は\(\small{ \ y=x \ }\)上にあるから
\(\small{ \begin{eqnarray}
\left\{
\begin{array}{l}
\displaystyle\frac{b-q}{a-p}\cdot(-1)=-1\\
\displaystyle\frac{b+q}{2}=-\displaystyle\frac{a+p}{2}
\end{array}
\right.
\end{eqnarray}\ }\)

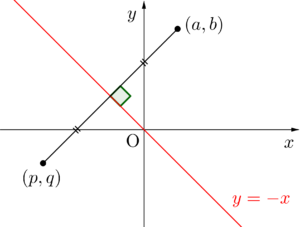
これを式変形すると
\(\small{ \begin{eqnarray}
\left\{
\begin{array}{l}
p-q=a-b \\
-p-q=a+b
\end{array}
\right.
\end{eqnarray} \ }\)
これを解いて、\(\small{ \ (p, \ q)=(-b, -a ) \ }\)になる。

つまり\(\small{ \ x \ }\)座標と\(\small{ \ y \ }\)座標を入れ替えて、符号を反転させたら\(\small{ \ y=-x \ }\)に関して対称移動するんだ。

これを関数に発展させると\(\small{ \ y=f(x) \ }\)を\(\small{ \ y=-x \ }\)に関して対称移動した関数は\(\small{ \ -x=f(-y) \ }\)になるんだ。

原点周りに回転移動

次は点\(\small{ \ \mathrm{A}(a, \ b) \ }\)を原点周りに\(\small{ \ \theta \ }\)回転させる移動について考えていこう。

原点\(\small{ \ \mathrm{O} \ }\)と点\(\small{ \ \mathrm{A}(a, \ b) \ }\)を結ぶ線分\(\small{ \ \mathrm{OA} \ }\)と\(\small{ \ x \ }\)軸のなす角を\(\small{ \ \alpha \ }\)とすると
\(\small{ \ \cos \alpha=\displaystyle\frac{a}{\mathrm{OA}}=\displaystyle\frac{a}{\sqrt{a^2+b^2}} \ }\)
\(\small{ \ \sin \alpha=\displaystyle\frac{b}{\mathrm{OA}}=\displaystyle\frac{b}{\sqrt{a^2+b^2}} \ }\)

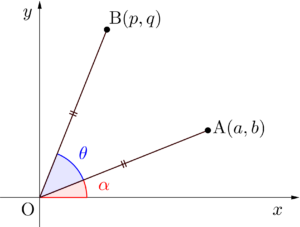
点\(\small{ \ \mathrm{A}(a, \ b) \ }\)を原点周りに\(\small{ \ \theta \ }\)回転させた点を\(\small{ \ \mathrm{B}(p, \ q) \ }\)とすると
\(\small{ \ p=\sqrt{a^2+b^2}\cos \left(\theta+\alpha\right) \ }\)
\(\small{ \ q=\sqrt{a^2+b^2}\sin \left(\theta+\alpha\right) \ }\)
になる。

さらに

つまり\(\small{ \ (a, \ b) \ }\)を原点周りに\(\small{ \ \theta \ }\)回転させた点\(\small{ \ (p, \ q) \ }\)は

になるんだ。

回転については複素数平面（数学Ⅲ）で考えると

\(\small{\begin{eqnarray} \ p+qi&=&(a+bi)(\cos \theta+i\sin \theta)\\[3pt] &=&a\cos \theta-b\sin \theta+(a\sin \theta+b\cos \theta)i \ \end{eqnarray}}\)

って簡単に求めることもできるからね。

Point 点の移動

①点の移動の式を導けるようにする
②関数への発展を考える