こんにちは、リンス(@Lins016)です。
今回はガウス記号について学習していこう。
ガウス記号って何?
ガウス記号って聞いたことある人もいると思うけど、どんな記号かというと\(\small{ \ \lbrack x \rbrack \ }\)って書いて、\(\small{ \ x \ }\)を超えない最大の整数を表すんだ。
この括弧で表された記号のことをガウス記号っていうんだ。
つまり\(\small{ \ \lbrack 2.1 \rbrack=2 \ }\)、\(\small{ \ \lbrack 2 \rbrack=2 \ }\)、\(\small{ \ \lbrack 1.9 \rbrack=1 \ }\)になるんだ。
ガウス記号
\(\small{ \ x \ }\)を超えない最大の整数を\(\small{ \ \lbrack x \rbrack \ }\)と表す
ガウス記号の性質
\(\small{ \ \lbrack x \rbrack=n \ }\)のとき (ただし、\(\small{ \ n \ }\)は整数)
\(\small{ \ n \leqq x \lt n+1\Leftrightarrow \lbrack x \rbrack \leqq x \lt \lbrack x \rbrack+1 \ }\)
\(\small{ \ x-1\lt n \leqq x\Leftrightarrow x-1\lt \lbrack x \rbrack \leqq x \ }\)
\(\small{ \ \lbrack x+y \rbrack\geqq \lbrack x \rbrack+\lbrack y \rbrack \ }\)
ガウス記号の不等式
まずはガウス記号の性質について考えてみよう。
\(\small{ \ \lbrack x \rbrack \ }\)は\(\small{ \ x \ }\)を超えない最大の整数を表すんだから、\(\small{ \ \lbrack x \rbrack=2 \ }\)なら\(\small{ \ 2\leqq x \lt 3 \ }\)が言えるよね。
つまり一般化すると\(\small{ \ \lbrack x \rbrack=n \ }\)なら\(\small{ \ n\leqq x \lt n+1 \ }\)が言える。
\(\small{ \ n=\lbrack x \rbrack \ }\)だから\(\small{ \ \lbrack x \rbrack\leqq x \lt \lbrack x \rbrack+1 \ }\)になるよね。
次にこの不等式を変形してみよう。
\(\small{ \ n \ }\)を基準にすると\(\small{ \ \lbrack x \rbrack=n \ }\)は\(\small{ \ x-1\lt n \leqq x \ }\)になるんだ。
さっきと同じように\(\small{ \ n=\lbrack x \rbrack \ }\)だから\(\small{ \ x-1\lt \lbrack x \rbrack \leqq x \ }\)になるよね。
これは\(\small{ \ \lbrack x \rbrack=n \ }\)の\(\small{ \ x \ }\)を基準にするか\(\small{ \ n \ }\)を基準にするかの違いだけど、よく出題されるからどちらの不等式も覚えておこう。
ガウス記号の小数部分
\(\small{ \ \lbrack x \rbrack=n \ }\)のとき\(\small{ \ n \ }\)は\(\small{ \ x \ }\)の整数部分になる。だから\(\small{ \ x \ }\)の小数部分は\(\small{ \ x-\lbrack x \rbrack \ }\)って書けるよね。
入試では「\(\small{ \ x \ }\)の小数部分を\(\small{ \ \langle x \rangle \ }\)とする」ってなって、記号で小数部分を定義する問題もあるけど、これもガウス記号を使うと\(\small{ \ x-\lbrack x \rbrack \ }\)って書けるからガウス記号の問題として考えられるよね。
ちなみにこの整数部分、小数部分って「\(\small{ \ N=\displaystyle\frac{1}{3-\sqrt{5}} \ }\)の整数部分を\(\small{ \ a \ }\)、小数部分を\(\small{ \ b \ }\)とする」って問題に似ているよね。
\(\small{ \ N=a+b \ }\)だし、\(\small{ \ x=\lbrack x \rbrack+\langle x \rangle \ }\)だもんね。
ガウス記号とグラフ
ガウス記号のグラフについて考えてみよう。
とにかく\(\small{ \ \lbrack x \rbrack \ }\)は\(\small{ \ x \ }\)を超えない最大の整数なんだから、\(\small{ \ \lbrack 2.1 \rbrack=\lbrack 2.2 \rbrack=\lbrack 2.3 \rbrack=2 \ }\)のように整数部分が変化しなかったら常に一定の値になるんだ。
だからそのことを考慮してグラフを書いてみよう。
まずはガウス記号を外したグラフ(\(\small{ \ y=\lbrack x \rbrack \ }\)なら\(\small{ \ y=x \ }\))を薄く鉛筆で書いて(または破線でも)、\(\small{ \ y \ }\)座標の整数部分が変化する点に注意してグラフを書こう。
ガウス記号がどんなグラフを描くのかってことはきちんとおさえておこう。
\(\small{ \ y=\lbrack x \rbrack \ }\)
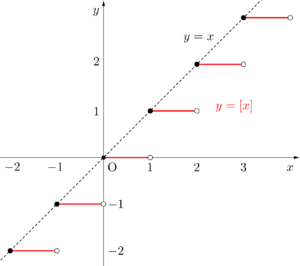
\(\small{ \ y=\lbrack 2x \rbrack \ }\)
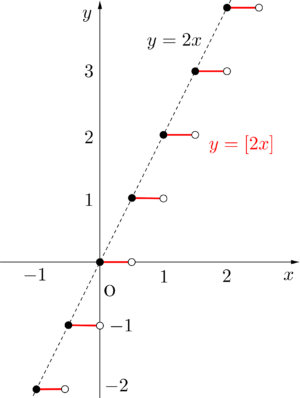
\(\small{ \ y=\lbrack x^2 \rbrack \ }\)
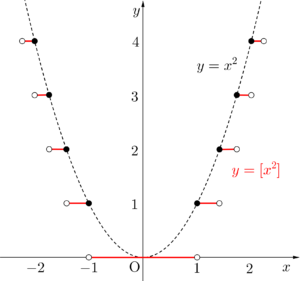
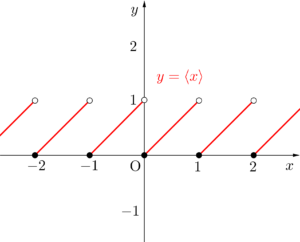
小数部分のグラフは次のようになるからね。
\(\small{\begin{eqnarray} \ y&=&\langle x \rangle\\[3pt] &=&x-\lbrack x \rbrack \ \end{eqnarray}}\)
(1)\(\small{ \ \lbrack 2x+1 \rbrack=4 \ }\)を満たす\(\small{ \ x \ }\)の範囲を求めよ。
(2)\(\small{ \ \lbrack x+1 \rbrack=\displaystyle\frac{1}{2}x+3 \ }\)を解け。
(1)\(\small{ \ \lbrack 2x+1 \rbrack=4 \ }\)より\(\small{ \ 4\leqq 2x+1 \lt 5 \ }\)
これを解いて\(\small{ \ \displaystyle\frac{3}{2}\leqq x \lt 2 \ }\)
(2)\(\small{ \ \lbrack x+1 \rbrack \ }\)は\(\small{ \ x \lt \lbrack x+1 \rbrack \leqq x+1 \ }\)より
\(\small{ \ x \lt \displaystyle\frac{1}{2}x+3 \leqq x+1 \ }\)
これを解くと\(\small{ \ 4\leqq x \lt 6 \ }\)
(i)\(\small{ \ 4\leqq x \lt 5 \ }\)のとき\(\small{ \ \lbrack x+1 \rbrack=5 \ }\)
\(\small{ \ \displaystyle\frac{1}{2}x+3=5 \ }\)
\(\small{ \ \therefore x=4 \ }\)
(ii)\(\small{ \ 5\leqq x \lt 6 \ }\)のとき\(\small{ \ \lbrack x+1 \rbrack=6 \ }\)
\(\small{ \ \displaystyle\frac{1}{2}x+3=6 \ }\)
\(\small{ \ x=6 \ }\) \(\small{ \ 5\leqq x \lt 6 \ }\)より不適
(i)(ii)より\(\small{ \ x=4 \ }\)

Point ガウス記号
①ガウス記号の性質をおさえる
②二つの不等式を導ける
③ガウス記号のグラフを覚える
正の数\(\small{ \ p \ }\)に対して、\(\small{ \ p \ }\)の整数部分、小数部分をそれぞれ\(\small{ \ \lbrack p \rbrack, \ \langle x \rangle \ }\)とする。
例えば\(\small{ \ \lbrack 3.14\rbrack=3, \ \langle 3.14 \rangle=0.14 \ }\)である。
自然数\(\small{ \ n \ }\)に対して、\(\small{ \ x \ }\)の二次方程式\(\small{ \ x^2-nx-1=0 \ }\)の解で正のものを\(\small{ \ \alpha \ }\)とする。\(\small{ \ n^2\lt n^2+4 \lt n^2+4n+4 \ }\)である。
このとき次の値を求めよ。
(1)\(\small{ \ \alpha \ }\)
(2)\(\small{ \ \lbrack \alpha \rbrack \ }\)
(3)\(\small{ \ \langle \alpha \rangle \ }\)
(4)\(\small{ \ \lbrack \displaystyle\frac{1}{\alpha} \rbrack \ }\)
(5)\(\small{ \ \langle \displaystyle\frac{1}{\alpha} \rangle \ }\)
(6)\(\small{ \ \lbrack \displaystyle\frac{1}{\langle \alpha \rangle} \rbrack \ }\)
(7)\(\small{ \ \langle \displaystyle\frac{1}{\langle \alpha \rangle} \rangle \ }\)
(1)
\(\small{ \ x^2-nx-1=0 \ }\)
\(\small{ \ \alpha\gt0 \ }\)より\(\small{ \ x=\displaystyle\frac{n+\sqrt{n^2+4}}{2} \ }\)
(2)
\(\small{ \ n^2\lt n^2+4 \lt n^2+4n+4 \ }\)
\(\small{ \ n\lt \sqrt{n^2+4}\lt n+2 \ }\)
\(\small{ \ n\lt \displaystyle\frac{n+\sqrt{n^2+4}}{2}\lt n+1 \ }\)
\(\small{\begin{eqnarray} \ \lbrack \alpha \rbrack&=&\lbrack \displaystyle\frac{n+\sqrt{n^2+4}}{2} \rbrack\\[3pt]
&=&n \ \end{eqnarray}}\)
(3)
\(\small{ \ \langle \alpha \rangle=\alpha-\lbrack \alpha \rbrack \ }\)より
\(\small{\begin{eqnarray} \ \langle \alpha \rangle&=&\displaystyle\frac{n+\sqrt{n^2+4}}{2}-n\\[3pt]
&=&\displaystyle\frac{\sqrt{n^2+4}-n}{2} \ \end{eqnarray}}\)
(4)
\(\small{\begin{eqnarray} \ \displaystyle\frac{1}{\alpha}&=&\displaystyle\frac{2}{n+\sqrt{n^2+4}}\\[3pt]
&=&\displaystyle\frac{2(n-\sqrt{n^2+4})}{(n+\sqrt{n^2+4})(n-\sqrt{n^2+4})}\\[3pt]
&=&\displaystyle\frac{\sqrt{n^2+4}-n}{2} \ \end{eqnarray}}\)
ここで
\(\small{ \ 0\lt \sqrt{n^2+4}-n \lt 2 \ }\)より
\(\small{ \ 0\lt \displaystyle\frac{\sqrt{n^2+4}-n}{2}\lt 1 \ }\)
\(\small{\begin{eqnarray} \ \lbrack \displaystyle\frac{1}{\alpha} \rbrack&=&\lbrack \displaystyle\frac{\sqrt{n^2+4}-n}{2} \rbrack\\[3pt]
&=&0 \ \end{eqnarray}}\)
(5)
\(\small{\begin{eqnarray} \ \langle \displaystyle\frac{1}{\alpha} \rangle&=&\displaystyle\frac{1}{\alpha}-\lbrack \displaystyle\frac{1}{\alpha} \rbrack\\[3pt]
&=&\displaystyle\frac{\sqrt{n^2+4}-n}{2} \ \end{eqnarray}}\)
(6)
\(\small{\begin{eqnarray} \ \lbrack \displaystyle\frac{1}{\langle \alpha \rangle}\rbrack&=&\lbrack \displaystyle\frac{2}{\sqrt{n^2+4}- n}\rbrack\\[3pt]
&=&\lbrack \displaystyle\frac{\sqrt{n^2+4}+n}{2}\rbrack\\[3pt]
&=&n \ \end{eqnarray}}\)
(7)
\(\small{\begin{eqnarray} \ \langle \displaystyle\frac{1}{\langle \alpha \rangle}\rangle&=&\displaystyle\frac{1}{\langle \alpha \rangle}-\lbrack \displaystyle\frac{1}{\langle \alpha \rangle}\rbrack\\[3pt]
&=&\displaystyle\frac{\sqrt{n^2+4}+n}{2}-n\\[3pt]
&=&\displaystyle\frac{\sqrt{n^2+4}-n}{2} \ \end{eqnarray}}\)

