定積分と不等式

こんにちは、リンス(@Lins016)です。
今回は定積分と不等式について学習していこう。

定積分と不等式の解き方

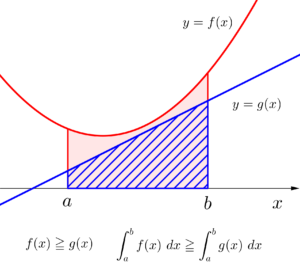
定積分が面積を表すとき、面積の大きさを比較して不等式を作ることが可能だよね。

区間\(\small{ \ [a, \ b] \ }\)で\(\small{ \ f(x)\geqq0 \ }\)なら\(\small{ \ \displaystyle\int_{a}^{b} \ f(x) \ dx\geqq0 \ }\)が言えるし、\(\small{ \ f(x)\geqq g(x) \ }\)なら\(\small{ \ \displaystyle\int_{a}^{b}f(x) \ dx\geqq \displaystyle\int_{a}^{b}g(x) \ dx \ }\)が言えるんだ。

特にこの\(\small{ \ \displaystyle\int_{a}^{b}f(x) \ dx\geqq \displaystyle\int_{a}^{b}g(x) \ dx \ }\)は入試でも使うから確実におさえておこう。

定積分と不等式

区間\(\small{ \ [a, \ b] \ }\)で\(\small{ \ f(x)\geqq0 \ }\)なら\(\small{ \ \displaystyle\int_{a}^{b} \ f(x) \ dx\geqq0 \ }\)

区間\(\small{ \ [a, \ b] \ }\)で\(\small{ \ f(x)\gt g(x) \ }\)なら\(\small{ \ \displaystyle\int_{a}^{b} \ f(x) \ dx \gt \displaystyle\int_{a}^{b} g(x) \ dx \ }\)

\(\small{ \ f(x) \ }\)が減少関数のとき
\(\small{ \ f(k+1) \lt \displaystyle\int_{k}^{k+1}f(x) \ dx\lt f(k) \ }\)

\(\small{ \ \displaystyle\int_{1}^{n+1}f(x) \ dx\lt f(1)+f(2)+\cdots+f(n)\lt \displaystyle\int_{0}^{n}f(x) \ dx \ }\)

\(\small{ \ f(x) \ }\)が増加関数のとき
\(\small{ \ f(k) \lt \displaystyle\int_{k}^{k+1}f(x) \ dx\lt f(k+1) \ }\)

\(\small{ \ \displaystyle\int_{0}^{n}f(x) \ dx\lt f(1)+f(2)+\cdots+f(n)\lt \displaystyle\int_{1}^{n+1}f(x) \ dx \ }\)

面積による比較

定積分の不等式は面積を利用した比較が一番簡単。

例えば、区間\(\small{ \ [a, \ b] \ }\)で\(\small{ \ f(x)\geqq g(x) \ }\)なら\(\small{ \ \displaystyle\int_{a}^{b} \ f(x) \ dx\geqq \displaystyle\int_{a}^{b} g(x) \ dx \ }\)になる。
これって面積を見たら明らかだよね。

「積分区間が同じとき」ってのも重要だから注意しよう。

定積分の和と不等式

定積分の面積を利用して不等式が作れるっていうのがわかったよね。今度はこれを応用した不等式の問題について考えてみよう。

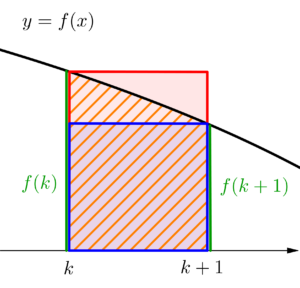
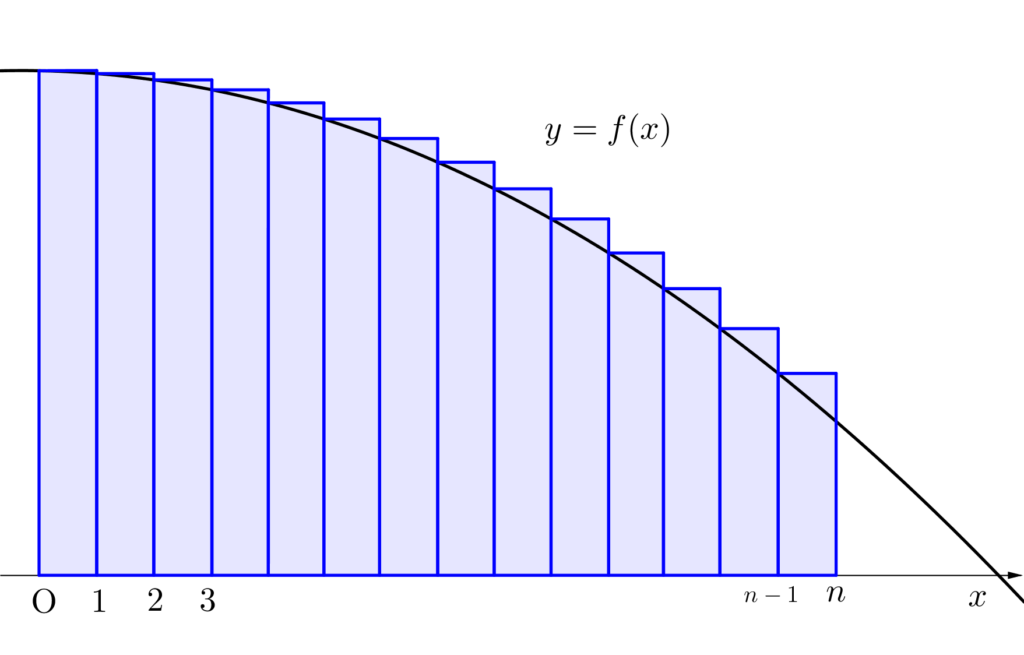
例えば、減少関数\(\small{ \ y=f(x) \ }\)があるとする。（減少関数っていうのは\(\small{ \ x \ }\)が増加すると\(\small{ \ y \ }\)が減少する関数のことね。）

自然数\(\small{ \ k \ }\)に対して\(\small{ \ k\leqq x \leqq k+1 \ }\)のとき、\(\small{ \ f(k+1)\leqq f(x) \leqq f(k) \ }\)が成り立つよね。

つまり、区間\(\small{ \ [k, \ k+1] \ }\)で\(\small{ \ f(k+1)\leqq f(x) \leqq f(k) \ }\)が成り立つから

\(\small{ \ \displaystyle\int_{k}^{k+1}f(k+1) \ dx\leqq \displaystyle\int_{k}^{k+1}f(x) \ dx\leqq\displaystyle\int_{k}^{k+1}f(k) \ dx \ }\)

が成り立つ。

しかも常に\(\small{ \ f(k)=f(x)=f(k+1) \ }\)が成り立つわけじゃないから

\(\small{ \ \displaystyle\int_{k}^{k+1}f(k+1) \ dx\lt \displaystyle\int_{k}^{k+1}f(x) \ dx\lt\displaystyle\int_{k}^{k+1}f(k) \ dx \ }\)

になるんだ。

ちなみに\(\small{ \ \displaystyle\int_{k}^{k+1}f(k) \ dx=f(k) \ }\)（赤枠の長方形）だし、\(\small{ \ \displaystyle\int_{k}^{k+1}f(k+1) \ dx=f(k+1) \ }\)（青枠の長方形）だから\(\small{ \ f(k+1)\lt \displaystyle\int_{k}^{k+1}f(x) \ dx\lt f(k) \ }\)ってことになる。
\(\small{ \ \displaystyle\int_{k}^{k+1}f(x) \ dx \ }\)はオレンジの斜線部分ね。

これって図から考えても明らかだよね。

この不等式\(\small{ \ f(k+1)\lt \displaystyle\int_{k}^{k+1}f(x) \ dx\lt f(k) \ }\)を
\(\small{ \ \begin{eqnarray}
\left\{
\begin{array}{l}
\displaystyle\int_{k}^{k+1}f(x) \ dx\lt f(k)\cdots①\\
\displaystyle\int_{k}^{k+1}f(x) \ dx\gt f(k+1)\cdots②
\end{array}
\right.
\end{eqnarray} \ }\)
に分けて考えていこう。

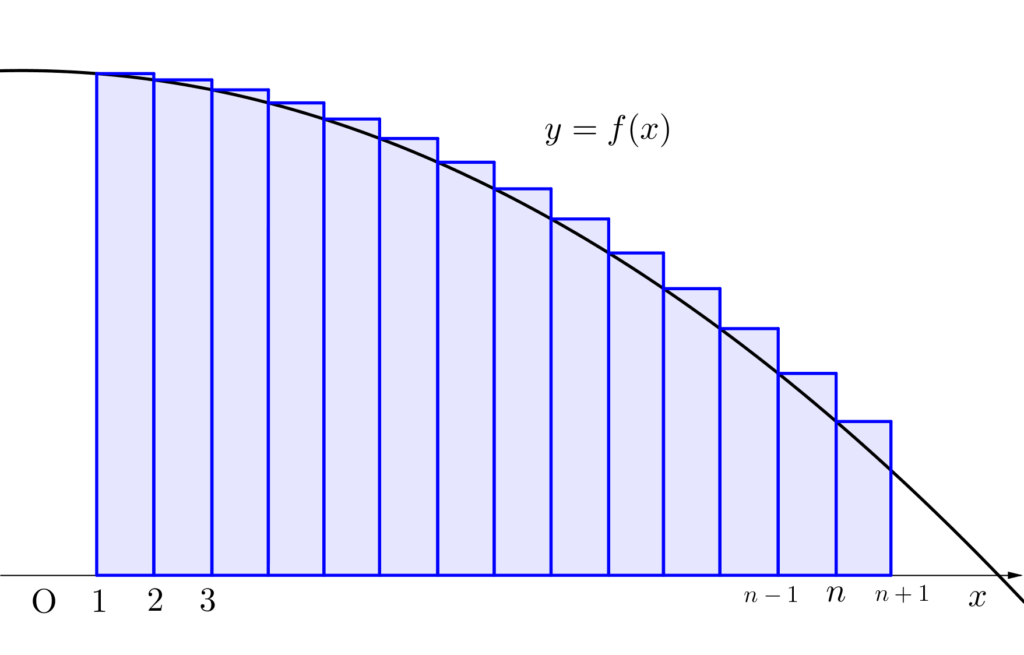
まずは\(\small{①}\)の\(\small{ \ \displaystyle\int_{k}^{k+1}f(x) \ dx\lt f(k) \ }\)の\(\small{ \ k \ }\)に\(\small{ \ k=1, \ 2, \ 3\cdots, \ n \ }\)を代入してみよう。
\(\small{\begin{array}{r} \ \displaystyle\int_{1}^{2}f(x) \ dx&\lt f(1)\\[3pt] \displaystyle\int_{2}^{3}f(x) \ dx&\lt f(2)\\[3pt] \displaystyle\int_{3}^{4}f(x) \ dx&\lt f(3)\\[3pt] \vdots&\\[3pt] \displaystyle\int_{n}^{n+1}f(x) \ dx&\lt f(n)\end{array}}\)

次にこの式を辺々加えてみよう。

\(\small{ \ \displaystyle\int_{1}^{2}f(x) \ dx +\displaystyle\int_{2}^{3}f(x) \ dx+\displaystyle\int_{3}^{4}f(x) \ dx+\cdots+\displaystyle\int_{n}^{n+1}f(x) \ dx\lt f(1)+f(2)+(3)+\cdots+f(n) \ }\)

このとき右辺に注目すると

\(\small{ \ \displaystyle\int_{1}^{2}f(x) \ dx +\displaystyle\int_{2}^{3}f(x) \ dx+\displaystyle\int_{3}^{4}f(x) \ dx+\cdots+\displaystyle\int_{n}^{n+1}f(x) \ dx=\displaystyle\int_{1}^{n+1}f(x) \ dx \ }\)

になるから

\(\small{ \ \displaystyle\int_{1}^{n+1}f(x) \ dx\lt f(1)+f(2)+(3)+\cdots+f(n)\cdots③ \ }\)

が言えるんだ。この\(\small{ \ ③}\)の式って下の図で成り立つのが確認できるよね。

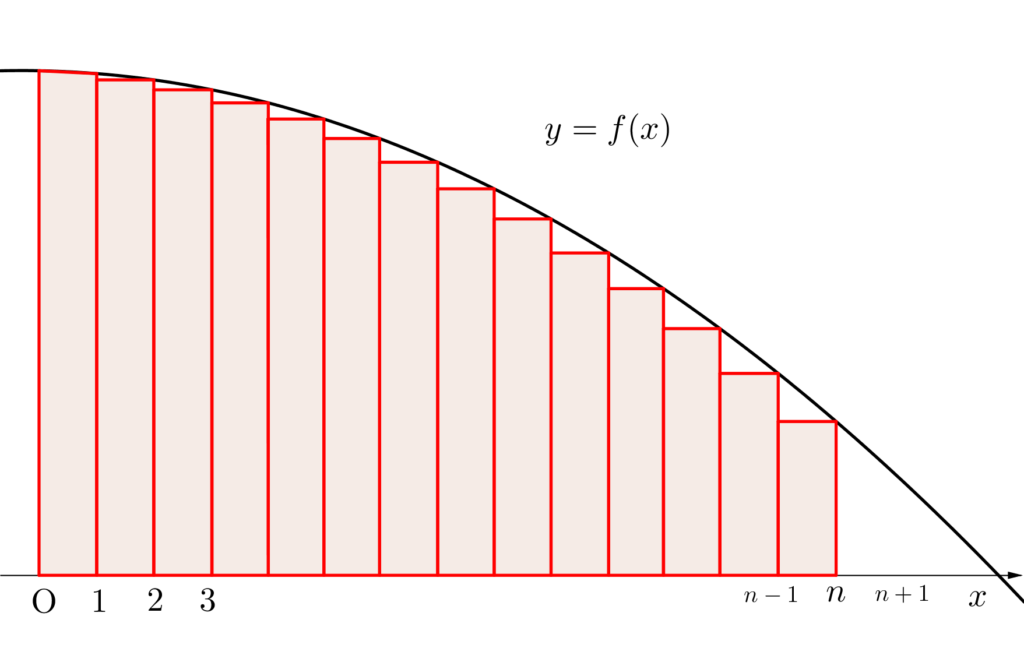
次は\(\small{②}\)の\(\small{ \ \displaystyle\int_{k}^{k+1}f(x) \ dx\gt f(k+1) \ }\)の\(\small{ \ k \ }\)に\(\small{ \ k=0, \ 1, \ 2\cdots, \ n-1 \ }\)を代入してみよう。
\(\small{\begin{array}{r} \ \displaystyle\int_{0}^{1}f(x) \ dx&\gt f(1)\\[3pt] \displaystyle\int_{1}^{2}f(x) \ dx&\gt f(2)\\[3pt] \displaystyle\int_{2}^{3}f(x) \ dx&\gt f(3)\\[3pt] \vdots&\\[3pt] \displaystyle\int_{n-1}^{n}f(x) \ dx&\gt f(n) \ \end{array}}\)

次にこの式を辺々加えてみよう。

\(\small{ \ \displaystyle\int_{0}^{1}f(x) \ dx +\displaystyle\int_{1}^{2}f(x) \ dx+\displaystyle\int_{2}^{3}f(x) \ dx+\cdots+\displaystyle\int_{n-1}^{n}f(x) \ dx\gt f(1)+f(2)+(3)+\cdots+f(n) \ }\)

このとき右辺に注目すると

\(\small{ \ \displaystyle\int_{1}^{2}f(x) \ dx +\displaystyle\int_{2}^{3}f(x) \ dx+\displaystyle\int_{3}^{4}f(x) \ dx+\cdots+\displaystyle\int_{n-1}^{n}f(x) \ dx=\displaystyle\int_{0}^{n}f(x) \ dx \ }\)

になるから

\(\small{ \ \displaystyle\int_{0}^{n}f(x) \ dx\gt f(1)+f(2)+(3)+\cdots+f(n)\cdots④ \ }\)

が言えるんだ。

この\(\small{ \ ④}\)の式って下の図で成り立つのが確認できるよね。

つまり\(\small{ \ ③, \ ④ \ }\)から

\(\small{ \ \displaystyle\int_{1}^{n+1}f(x) \ dx\lt f(1)+f(2)+(3)+\cdots+f(n)\lt \displaystyle\int_{0}^{n}f(x) \ dx \ }\)

が言えるんだ。

これが面積を利用した不等式の証明になる。

一つ注意しておきたいのが
\(\small{ \ f(k+1)\leqq f(x) \leqq f(k)\cdots① \ }\)の式から

\(\small{ \ \displaystyle\int_{k}^{k+1}f(k+1) \ dx\lt \displaystyle\int_{k}^{k+1}f(x) \ dx\lt\displaystyle\int_{k}^{k+1}f(k) \ dx\cdots② \ }\)

を導いて

\(\small{ \ \displaystyle\int_{1}^{n+1}f(x) \ dx\lt f(1)+f(2)+(3)+\cdots+f(n)\lt \displaystyle\int_{0}^{n}f(x) \ dx\cdots④ \ }\)

を証明するんだけど、
\(\small{ \ ② \ }\)の不等式の形を保って\(\small{ \ ③ \ }\)を導いたわけじゃないんだ。\(\small{ \ ② \ }\)の式を\(\small{ \ 2 \ }\)つに分解するってところがポイントだからね。

この不等式は減少関数を利用した証明だったけど、もちろん関数が増加関数の場合も同じような形で証明出来る。だけど関数が増加したり減少したりする関数だと同じような証明はできないから注意しよう。だって
\(\small{ \ \displaystyle\int_{0}^{1}f(x) \ dx\lt f(1) \ }\)
\(\small{ \ \displaystyle\int_{1}^{2}f(x) \ dx\gt f(2) \ }\)
って不等号の向きが逆になったりすると辺々足したときどっちが大きくなるかわからないからね。

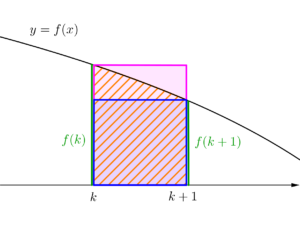
同じ区間での面積の比較

上の方法は

\(\small{ \ \displaystyle\int_{1}^{n+1}f(x) \ dx\lt f(1)+f(2)+(3)+\cdots+f(n)\lt \displaystyle\int_{0}^{n}f(x) \ dx \ }\)

って長方形の和を基準（不等式の真ん中）にして証明したけど、今度は積分の方を基準に考えてみよう。

さっきと同じ減少関数の場合、下図を考えると

\(\small{ \ f(1)+f(2)+(3)+\cdots+f(n)\lt \displaystyle\int_{0}^{n}f(x) \ dx \lt f(0)+f(1)+(2)+\cdots+f(n-1) \ }\)

が言えるよね。

下の図なら

\(\small{ \ f(2)+f(3)+(4)+\cdots+f(n+1)\lt \displaystyle\int_{1}^{n+1}f(x) \ dx \lt f(1)+f(2)+(3)+\cdots+f(n) \ }\)

が言えるよね。

\(\small{ \ f(k+1)\lt \displaystyle\int_{k}^{k+1}f(x) \ dx\lt f(k) \ }\)の式に\(\small{ \ k=0,1,2\cdots,n-1 \ }\)を代入した式を足したものが

\(\small{ \ f(1)+f(2)+(3)+\cdots+f(n)\lt \displaystyle\int_{0}^{n}f(x) \ dx \lt f(0)+f(1)+(2)+\cdots+f(n-1) \ }\)

になるし、\(\small{ \ k=1,2,3\cdots,n \ }\)を代入したものが

\(\small{ \ f(2)+f(3)+(4)+\cdots+f(n+1)\lt \displaystyle\int_{1}^{n+1}f(x) \ dx \lt f(1)+f(2)+(3)+\cdots+f(n) \ }\)

になるんだ。

最初の不等式を分けて考えるより、単に代入するだけで済むこっちの方が簡単だって思ったかもしれないけど、実際の問題は長方形の和が不等式の基準（不等式の真ん中）になってることが多いから、こんな単純に\(\small{ \ k \ }\)に値を代入して比較できる問題はあまりないんだ。

でもこの考え方もきちんとマスターしておこう。
さらにこの\(\small{ \ 2 \ }\)つの考え方を図にすると次の図になるから覚えておこう。

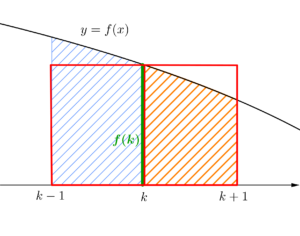
曲線の面積を長方形の面積で比較
\(\small{ \ f(k+1)\lt\displaystyle\int_{k}^{k+1}f(x) \ dx \lt f(k) \ }\)

長方形の面積を曲線の面積で比較
\(\small{ \ \displaystyle\int_{k}^{k+1}f(x) \ dx\lt f(k) \lt\displaystyle\int_{k-1}^{k}f(x) \ dx \ }\)

例題を確認

問題解答

次の不等式を証明せよ。

\(\small{ \ 2(\sqrt{n+1}-1)\lt1+\displaystyle\frac{1}{\sqrt{2}}+\cdots+\displaystyle\frac{1}{\sqrt{n}}\leqq 2\sqrt{n}-1 \ }\)

自然数\(\small{ \ k \ }\)に対して\(\small{ \ k\leqq x \leqq k+1 \ }\)のとき、\(\small{ \ y=\displaystyle\frac{1}{\sqrt{x}} \ }\)は減少関数より
\(\small{ \ \displaystyle\frac{1}{\sqrt{k+1}}\leqq \displaystyle\frac{1}{\sqrt{x}} \leqq \displaystyle\frac{1}{\sqrt{k}} \ }\)

\(\small{ \ \displaystyle\int_{k}^{k+1}\displaystyle\frac{1}{\sqrt{k+1}} \ dx \leqq \displaystyle\int_{k}^{k+1} \displaystyle\frac{1}{\sqrt{x}} \ dx \leqq \displaystyle\int_{k}^{k+1}\displaystyle\frac{1}{\sqrt{k}} \ dx \ }\)

\(\small{ \ \therefore \displaystyle\frac{1}{\sqrt{k+1}}\leqq \displaystyle\int_{k}^{k+1} \displaystyle\frac{1}{\sqrt{x}} \ dx \leqq \displaystyle\frac{1}{\sqrt{k}} \ }\)
しかも\(\small{ \ \displaystyle\frac{1}{\sqrt{x}}=\displaystyle\frac{1}{\sqrt{k}}=\displaystyle\frac{1}{\sqrt{k+1}} \ }\)は常に成り立つわけじゃないから
\(\small{ \ \displaystyle\frac{1}{\sqrt{k+1}}\lt \displaystyle\int_{k}^{k+1} \displaystyle\frac{1}{\sqrt{x}} \ dx \lt \displaystyle\frac{1}{\sqrt{k}} \ }\)
\(\small{ \ \begin{eqnarray}
\left\{
\begin{array}{l}
\displaystyle\frac{1}{\sqrt{k+1}}\lt \displaystyle\int_{k}^{k+1} \displaystyle\frac{1}{\sqrt{x}} \ dx\cdots① \\
\displaystyle\frac{1}{\sqrt{k}}\gt \displaystyle\int_{k}^{k+1} \displaystyle\frac{1}{\sqrt{x}} \ dx\cdots②
\end{array}
\right.
\end{eqnarray} \ }\)
\(\small{①}\)に\(\small{ \ k=1, \ 2, \ \cdots, \ n-1 \ }\)を代入した式を辺々加えると

\(\small{ \ \displaystyle\frac{1}{\sqrt{2}}+\displaystyle\frac{1}{\sqrt{3}}+\cdots+\displaystyle\frac{1}{\sqrt{n}}\lt \displaystyle\int_{1}^{2} \displaystyle\frac{1}{\sqrt{x}} \ dx+\displaystyle\int_{2}^{3} \displaystyle\frac{1}{\sqrt{x}} \ dx+\cdots+\displaystyle\int_{n-1}^{n} \displaystyle\frac{1}{\sqrt{x}} \ dx \ }\)

ここで

\(\small{ \ \displaystyle\int_{1}^{2} \displaystyle\frac{1}{\sqrt{x}} \ dx+\displaystyle\int_{2}^{3} \displaystyle\frac{1}{\sqrt{x}} \ dx+\cdots+\displaystyle\int_{n-1}^{n} \displaystyle\frac{1}{\sqrt{x}} \ dx=\displaystyle\int_{1}^{n}\displaystyle\frac{1}{\sqrt{x}} dx \ }\)

\(\small{\begin{eqnarray} \ \displaystyle\int_{1}^{n}\displaystyle\frac{1}{\sqrt{x}} dx&=&\displaystyle\int_{1}^{n} x^{-\textstyle\frac{1}{2}}dx\\[3pt] &=&\left[2\sqrt{x}\right]_{1}^{n}\\[3pt] &=&2(\sqrt{n}-1) \ \end{eqnarray}}\)
よって

\(\small{ \ \displaystyle\frac{1}{\sqrt{2}}+\displaystyle\frac{1}{\sqrt{3}}+\cdots+\displaystyle\frac{1}{\sqrt{n}}\lt 2(\sqrt{n}-1) \ }\)ただし、\(\small{ \ n\geqq2 \ }\)

両辺に\(\small{ \ 1 \ }\)を加えると

\(\small{ \ 1+\displaystyle\frac{1}{\sqrt{2}}+\displaystyle\frac{1}{\sqrt{3}}+\cdots+\displaystyle\frac{1}{\sqrt{n}}\lt 2\sqrt{n}-1 \ }\)

\(\small{ \ n=1 \ }\)のとき左辺＝右辺が成り立つので

\(\small{ \ 1+\displaystyle\frac{1}{\sqrt{2}}+\displaystyle\frac{1}{\sqrt{3}}+\cdots+\displaystyle\frac{1}{\sqrt{n}}\leqq 2\sqrt{n}-1 \ }\)

ただし等号成立は\(\small{ \ n=1 \ }\)のとき
\(\small{②}\)に\(\small{ \ k=1, \ 2, \ \cdots, \ n \ }\)を代入した式を辺々加えると

\(\small{ \ 1+\displaystyle\frac{1}{\sqrt{2}}+\cdots+\displaystyle\frac{1}{\sqrt{n}}\gt \displaystyle\int_{1}^{2} \displaystyle\frac{1}{\sqrt{x}} \ dx+\displaystyle\int_{2}^{3} \displaystyle\frac{1}{\sqrt{x}} \ dx+\cdots+\displaystyle\int_{n}^{n+1} \displaystyle\frac{1}{\sqrt{x}} \ dx \ }\)

ここで

\(\small{ \ \displaystyle\int_{1}^{2} \displaystyle\frac{1}{\sqrt{x}} \ dx+\displaystyle\int_{2}^{3} \displaystyle\frac{1}{\sqrt{x}} \ dx+\cdots+\displaystyle\int_{n}^{n+1} \displaystyle\frac{1}{\sqrt{x}} \ dx=\displaystyle\int_{1}^{n}\displaystyle\frac{1}{\sqrt{x}} dx \ }\)

\(\small{ \ 1+\displaystyle\frac{1}{\sqrt{2}}+\cdots+\displaystyle\frac{1}{\sqrt{n}}\gt 2(\sqrt{n}-1) \ }\)

\(\small{ \ ③, \ ④ \ }\)より

\(\small{ \ 2(\sqrt{n+1}-1)\lt1+\displaystyle\frac{1}{\sqrt{2}}+\cdots+\displaystyle\frac{1}{\sqrt{n}}\leqq 2\sqrt{n}-1 \ }\)

は成り立つ

\(\small{ \ y=\displaystyle\frac{1}{\sqrt{x}} \ }\)を積分するとき積分区間を\(\small{ \ [0, \ n] \ }\)にはできないよね。だってこの関数の定義域は\(\small{ \ x \gt0 \ }\)だよね。だから積分区間は\(\small{ \ [1, \ n] \ }\)にしないといけない。
例えば\(\small{ \ y= \log x \ }\)も真数条件から \(\small{ \ x\gt0 \ }\)だから積分区間を\(\small{ \ [0, \ n] \ }\)にはできない。
\(\small{ \ [0, \ n] \ }\)で比較したい場合は\(\small{ \ [1, \ n] \ }\)で計算して、両辺に\(\small{ \ 1 \ }\)を加えたりして証明したい式と同じ形にしよう。

Point 定積分と不等式

①面積を利用して不等式を作る
②曲線で囲まれた面積と長方形の面積どちらを基準にするか考える

それじゃあ次は入試レベルの問題にチャレンジしてみよう。

入試レベルにチャレンジ

問題解答

正の整数\(\small{ \ n \ }\)の階乗の桁数を\(\small{ \ T(n) \ }\)とする。例えば\(\small{ \ n=5 \ }\)のとき、\(\small{ \ n!=120 \ }\)より\(\small{ \ T(5)=3 \ }\)とする。
(1)\(\small{ \ T(n) \ }\)を\(\small{ \ [\log_{10}n!] \ }\)を用いた式で表せ。ただし、実数\(\small{ \ x \ }\)に対し、\(\small{ \ [x] \ }\)は\(\small{ \ x \ }\)を超えない最大の整数を表す。
(2)任意の正の整数\(\small{ \ n \ }\)に対し、

\(\small{ \ \displaystyle\int_1^n \log_{10}x \ dx\lt T(n) \lt\displaystyle\int_1^{n+1}\log_{10}x \ dx +1 \ }\)

が成り立つことを示せ。
(3)\(\small{ \ \displaystyle\lim_{n\to \infty}\displaystyle\frac{T(n)}{n\log_{10}n} \ }\)を求めよ。

(1)\(\small{ \ n! \ }\)の桁数を\(\small{ \ p \ }\)とすると\(\small{ \ 10^{p-1}\leqq n! \lt 10^{p} \ }\)
底\(\small{ \ 10 \ }\)の対数をとると、
\(\small{ \ p-1\leqq \log_{10}n! \lt p \ }\)
\(\small{ \ \therefore [\log_{10}n!]=p-1 \ }\)
\(\small{ \ T(n)=p \ }\)より\(\small{ \ T(n)=[\log_{10}n!]+1 \ }\)

(2)

\(\small{ \ \log_{10}n!=\log_{10}1+\log_{10}2+\log_{10}3+\cdots+\log_{10}n \ }\)

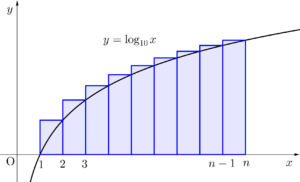
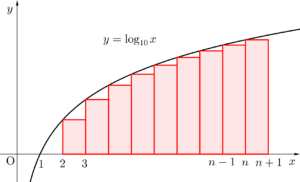
\(\small{ \ k \ }\)を正の自然数とすると\(\small{ \ y=\log_{10}x \ }\)は単調増加より
\(\small{ \ \log_{10}k\lt \displaystyle\int_k^{k+1}\log_{10}x \ dx \lt\log_{10}(k+1) \ }\)

\(\small{ \ \displaystyle\int_k^{k+1}\log_{10}x \ dx \lt \log_{10}(k+1) \ }\)
\(\small{ \ k=1,2,3,\cdots,n-1 \ }\)まで代入した式を辺々加えると
\(\small{ \ \displaystyle\int_1^{n}\log_{10}x \ dx \lt \log_{10}n! \ }\)
\(\small{ \ n=1 \ }\)のとき左辺＝右辺が成り立つから
\(\small{ \ \displaystyle\int_1^{n}\log_{10}x \ dx \leqq \log_{10}n! \ }\)

\(\small{ \ 0\leqq \log_{10}n!-[\log_{10}n!]\lt 1 \ }\)より
\(\small{ \ \log_{10}n!\lt [\log_{10}n!]+1 \ }\)
\(\small{ \ \therefore \displaystyle\int_1^{n}\log_{10}x \ dx \lt T(n) \ }\)

\(\small{ \ \log_{10}k\lt \displaystyle\int_k^{k+1}\log_{10}x \ dx \ }\)
\(\small{ \ k=1,2,3,\cdots,n \ }\)まで代入した式を辺々加えると
\(\small{ \ \log_{10}n!\lt \displaystyle\int_1^{n+1}\log_{10}x \ dx \ }\)

両辺に\(\small{ \ 1 \ }\)を加えて
\(\small{ \ \log_{10}n!+1\lt \displaystyle\int_1^{n+1}\log_{10}x \ dx+1 \ }\)
\(\small{ \ [\log_{10}n!]+1\lt \log_{10}n!+1 \ }\)より
\(\small{ \ T(n)\lt \log_{10}n!+1 \ }\)
\(\small{ \ \therefore T(n)\lt \displaystyle\int_1^{n+1}\log_{10}x \ dx+1 \ }\)
よって

\(\small{ \ \displaystyle\int_1^n \log_{10}x \ dx\lt T(n) \lt \displaystyle\int_1^{n+1}\log_{10}x \ dx +1 \ }\)

が成り立つ。

(3)

\(\small{ \ \displaystyle\int_{1}^{n} \log_{10}x \ dx\lt T(n) \lt \displaystyle\int_{1}^{n+1}\log_{10}x \ dx+1 \ }\)
\(\small{ \ \displaystyle\frac{\displaystyle\int_{1}^{n} \log_{10}x \ dx}{n\log_{10}n}\lt \displaystyle\frac{T(n)}{n\log_{10}n} \lt \displaystyle\frac{\displaystyle\int_{1}^{n+1}\log_{10}x \ dx+1}{n\log_{10}n} \ }\)

\(\small{ \ \displaystyle\frac{\displaystyle\int_{1}^{n} \log_{10}x \ dx}{n\log_{10}n}\\[3pt] =\displaystyle\frac{1}{n\log_{10}n}\displaystyle\int_{1}^{n} \log_{10}x \ dx\\[3pt] =\displaystyle\frac{\log 10}{n\log n} \displaystyle\int_{1}^{n} \displaystyle\frac{\log x}{\log 10} \ dx\\[3pt] =\displaystyle\frac{1}{n\log n}\left[x\log x-x\right]_1^n\\[3pt] = \displaystyle\frac{n\log n-n+1}{n\log n} \ }\)
\(\small{ \ \displaystyle\frac{\displaystyle\int_{1}^{n+1} \log_{10}x+1 \ dx}{n\log_{10}n}\\[3pt] =\displaystyle\frac{1}{n\log_{10}n} \left(\displaystyle\int_{1}^{n+1}\log_{10}x+1\right) \ dx\\[3pt] =\displaystyle\frac{\log 10}{n\log n} \left(\displaystyle\int_{1}^{n+1} \displaystyle\frac{\log x}{\log 10}+1\right) \ dx\\[3pt] =\displaystyle\frac{1}{n\log n}\left(\left[x\log x-x\right]_1^{n+1}+\log10\right)\\[3pt] = \displaystyle\frac{(n+1)\log (n+1)-n+\log10}{n\log n} \ }\)
よって
\(\small{ \ \displaystyle\lim_{n\to \infty}\displaystyle\frac{\displaystyle\int_{1}^{n} \log_{10}x \ dx}{n\log_{10}n}\\[3pt] = \displaystyle\lim_{n\to \infty} \displaystyle\frac{n\log n-n+1}{n\log n}\\[3pt] =1 \ }\)
\(\small{ \ \displaystyle\lim_{n\to \infty}\displaystyle\frac{\displaystyle\int_{1}^{n+1} \log_{10}x \ dx+1}{n\log_{10}n}\\[3pt] = \displaystyle\lim_{n\to \infty} \displaystyle\frac{(n+1)\log (n+1)-n+\log10}{n\log n}\\[3pt] =1 \ }\)
はさみうちの原理より
\(\small{ \ \displaystyle\lim_{n\to \infty}T(n)=1 \ }\)

\(\small{ \ x \ }\)を超えない最大の整数を\(\small{ \ [x] \ }\)で表す括弧の記号はガウス記号っていうんだったよね。教科書や定期試験にはあまり出題されないけど入試問題だと出題されるから確実におさえておこう。

CHECK

: ガウス記号
ガウス記号の性質やグラフ、小数部分の取り扱いについて詳しく解説しています。
続きを見る