こんにちは、リンス(@Lins016)です。
今回は高校数学と置換について学習していこう。
高校数学と置換
高校数学では置換して二次関数や三次関数、二次方程式や二次不等式、三次方程式に変形して問題を解くっていうのが、色々な単元で出題されるんだ。今回はどんな置換があるのか話していこう。
・二次関数
\(\small{ \ t=x^2 \ }\)
\(\small{ \ t=x^2-2x \ }\)
・三角関数
\(\small{ \ t=\sin \theta \ }\)
\(\small{ \ t=\sin \theta+\cos \theta \ }\)
・指数関数
\(\small{ \ t=a^x \ }\)
\(\small{ \ t=a^x+a^{-x} \ }\)
・対数関数
\(\small{ \ t=\log_a x \ }\)
置換と範囲(重要)
高校数学では『\(\small{ \ t=f(x) \ }\)とおく』ことで与えられた式が簡単に解けるようになったりする。高校\(\small{ \ 2 \ }\)年生以上だと、一度はおいたことあるよね。他の文字でおく置換について考えていこう。
まずどんな文字を置換するのか考える前に、一つ重要なことを覚えておこう。
それは「高校数学では置換したら、置換した文字の範囲を必ず考えないといけない」ってこと。つまり『\(\small{ \ t=x \ }\)の式』って置換したら\(\small{ \ t \ }\)には範囲が存在することになるんだ。
\(\small{ \ x \ }\)がすべての実数の範囲をとっても、\(\small{ \ t \ }\)は全ての実数の範囲をとるわけじゃない。
だから『\(\small{ \ t=x \ }\)の式とおく』って書いたら必ず\(\small{ \ t \ }\)の取りうる範囲を考えよう。\(\small{ \ t \ }\)の範囲を考えなくていい問題なんて\(\small{ \ 1 \ }\)つもないからね。
四次関数の置換
四次関数を置換する問題は\(\small{ \ 2 \ }\)つある。
それは「①\(\small{ \ x^4+x^2+1 \ }\)」と「②\(\small{ \ (x^2-2x)^2+4(x^2-2x)+3 \ }\)」の形の問題。
どちらも四次式だけど、置換することで二次式に変更することが出来るんだ。
①は\(\small{ \ t=x^2 \ }\)って置換すると\(\small{ \ t^2+t+1 \ }\)、②は\(\small{ \ t=x^2-2x \ }\)って置換すると\(\small{ \ t^2+4t+3 \ }\)になるよね。
だから四次関数なら二次関数に、四次方程式なら二次方程式にして解くことが出来るんだ。ただ最初に言ったように置換したら範囲が必ず変わるから、\(\small{ \ t \ }\)の範囲について考えないといけない。
\(\small{ \ t=x^2 \ }\)だと\(\small{ \ t\geqq0 \ }\)、\(\small{ \ t=x^2-2x \ }\)だと\(\small{ \ t=(x-1)^2-1 \ }\)だから\(\small{ \ t\geqq-1 \ }\)になるんだ。
\(\small{ \ t-x \ }\)グラフから\(\small{ \ t \ }\)の範囲を考えよう。
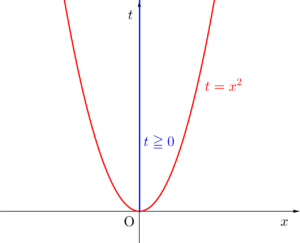
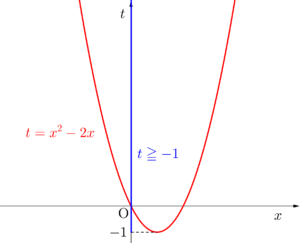
「\(\small{ \ t \ }\)の範囲を求める」ことは「\(\small{ \ t \ }\)の最大値・最小値を求める」ことと同じだから、二次関数の最大最小と言えば「平方完成してグラフ」だから、グラフを利用して\(\small{ \ t \ }\)の範囲を考えよう。

三角関数の置換
三角関数を置換する問題も大きく分けて\(\small{ \ 2 \ }\)つある。
それは「①\(\small{ \ \sin^2x+\sin x+1 \ }\)」と「②\(\small{ \ 2\sin x\cos x +\sin x+\cos x+2 \ }\)」の形の問題。
これも三角関数を\(\small{ \ t \ }\)と置換することで二次式に変更することが出来るんだ。
①は\(\small{ \ t=\sin x \ }\)って置換すると\(\small{ \ t^2+t+1 \ }\)、②は\(\small{ \ t=\sin x+ \cos x \ }\)って置換すると\(\small{ \ t^2=1+2\sin x\cos x \ }\)だから\(\small{ \ t^2+t+1 \ }\)になるよね。
①については\(\small{ \ t \ }\)を\(\small{ \ t=\cos x \ }\)や\(\small{ \ t=\tan x \ }\)っておくような問題もあるし、②については\(\small{ \ t \ }\)を\(\small{ \ t=\sqrt{3}\sin x+\cos x \ }\)っておくような問題もある。
これらの式が「\(\small{ \ y= \ }\)」なら二次関数に、「\(\small{ \ =0 \ }\)」なら二次方程式にして解くことが出来るんだ。ただこの場合も最初に言ったように、置換したら範囲が変わるから必ず範囲について考えないといけない。
特に\(\small{ \ x \ }\)の範囲が指定されていない場合、\(\small{ \ t=\sin x \ }\)だと\(\small{ \ -1\leqq t \leqq 1 \ }\)、\(\small{ \ t=\sin x+\cos x \ }\)だと\(\small{ \ t=\sqrt{2}\left(\sin x+\displaystyle\frac{\pi}{4}\right) \ }\)だから\(\small{ \ -\sqrt{2}\leqq t\leqq\sqrt{2} \ }\)になるんだ。
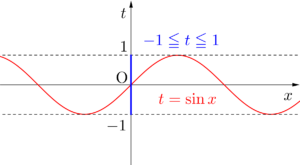
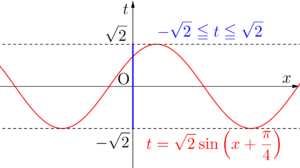
\(\small{ \ a\sin \theta+b\cos \theta \ }\)のような\(\small{ \ \sin \ }\)、\(\small{ \ \cos \ }\)の和・差は三角関数の合成を利用して範囲を求めよう。
三角関数の合成を忘れている人は下の記事で確認しておこう。
指数関数の置換
指数関数を置換する問題も大きく分けて\(\small{ \ 2 \ }\)つある。
それは「①\(\small{ \ 4^x+2^x+1 \ }\)」と「②\(\small{ \ 4^x+4^{-x} +2^x+2^{-x}+3 \ }\)」の形の問題。
これも指数関数を\(\small{ \ t \ }\)と置換することで二次式に変形することが出来るんだ。
①は\(\small{ \ t=2^x \ }\)って置換すると\(\small{ \ t^2+t+1 \ }\)になる。\(\small{ \ t=2^x \ }\)のとき、\(\small{ \ t^2 \ }\)は\(\small{ \ 2^{2x} \ }\)や\(\small{ \ 4^x \ }\)、\(\small{ \ (2^x)^2 \ }\)って表すことができる。
②は\(\small{ \ t=2^x+2^{-x} \ }\)って置換すると\(\small{ \ t^2=4^x+2+4^{-x} \ }\)だから\(\small{ \ t^2+t+1 \ }\)になるよね。
この場合も\(\small{ \ t^2 \ }\)は\(\small{ \ 4^x+4^{-x}+2 \ }\)や\(\small{ \ 2^{2x}+2^{-2x}+2 \ }\)って表すことができるからね。
だからこれらの式が「\(\small{ \ y= \ }\)」なら二次関数に、「\(\small{ \ =0 \ }\)」なら二次方程式にして解くことが出来るんだ。ただこの場合も最初に言ったように置換したら範囲が変わるから必ず範囲について考えないといけない。
\(\small{ \ t=2^x \ }\)のとき、\(\small{ \ t-x \ }\)グラフを考えて\(\small{ \ t\gt0 \ }\)になるよね。
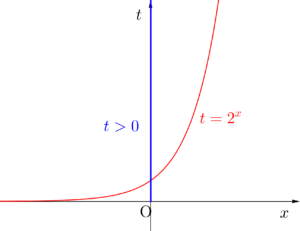
\(\small{ \ t=2^x+2^{-x} \ }\)は\(\small{ \ 2^x\gt0 \ }\)だから相加平均相乗平均の関係より\(\small{ \ 2^x+2^{-x}\geqq 2\sqrt{2^x\cdot2^{-x}}=2 \ }\)になるから\(\small{ \ t\geqq2 \ }\)になるんだ。必ず\(\small{ \ t \ }\)の範囲を考えるようにしよう。

対数関数の置換
対数関数を置換するのは基本的に\(\small{ \ 1 \ }\)つしかない。
それは「(対数)\(\small{^2 \ }\)」や「(対数)×(対数)」を見たとき、括弧内の対数を\(\small{ \ t \ }\)と置換しよう。
\(\small{ \ \left(\log_2x\right)^2-\log_2x^2+1 \ }\)なら\(\small{ \ t=\log_2x \ }\)とすると\(\small{ \ t^2-2t+1 \ }\)になるよね。
\(\small{ \ \left(\log_2\displaystyle\frac{x}{4}\right)\left(\log_2\displaystyle\frac{x}{8}\right) \ }\)なら\(\small{ \ \left(\log_2x-2\right)\left(\log_2x-3\right) \ }\)ってなるから\(\small{ \ t=\log_2x \ }\)とすれば\(\small{ \ (t-2)(t-3) \ }\)って表すことが出来るからね。
このときも\(\small{ \ t \ }\)の範囲に注意しよう。
この場合真数条件から\(\small{ \ x\gt0 \ }\)だよね。でも\(\small{ \ t \ }\)はすべての実数になるんだ。これも\(\small{ \ t-x \ }\)グラフを考えれば明らかだよね。

Point 高校数学と置換
①置換する文字の種類を覚える
②置換した文字の範囲を考える

「置換したら範囲を必ず考える」を癖にしておこう!
「\(\small{ \ t \ }\)=\(\small{ \ x \ }\)の式とおく」の「〜とおく」って書いたら必ず範囲を考えるの忘れないでね。

