こんにちは、リンス(@Lins016)です。
今回は三角関数の合成について学習していこう。
三角関数の合成のやり方
よく三角関数の合成を図を書いて単純に求めている人って見かけるよね。
確かに簡単に求められていいと思うけど、なんでその図から合成の形に変形できるのかってことを分かってない人が多いんじゃないかな?
今回は三角関数の合成をより深く考えてみよう。
・三角関数の合成(sin型)
\(\small{ \ a\sin\theta+b\cos\theta=\sqrt{a^2+b^2}\sin\left(\theta+\alpha\right) \ }\)
ただし、\(\small{ \ \cos\alpha=\displaystyle\frac{a}{\sqrt{a^2+b^2}} \ }\)、\(\small{ \ \sin\alpha=\displaystyle\frac{b}{\sqrt{a^2+b^2}} \ }\)
・三角関数の合成(cos型)
\(\small{ \ a\sin\theta+b\cos\theta=\sqrt{a^2+b^2}\cos\left(\theta-\alpha\right) \ }\)
ただし、\(\small{ \ \sin\alpha=\displaystyle\frac{a}{\sqrt{a^2+b^2}} \ }\)、\(\small{ \ \cos\alpha=\displaystyle\frac{b}{\sqrt{a^2+b^2}} \ }\)
・三角関数の合成と加法定理
\(\small{ \ a\sin\theta+b\cos\theta \ }\)
合成↓ ↑加法定理
\(\small{ \ \sqrt{a^2+b^2}\sin\left(\theta+\alpha\right) \ }\)
三角関数の合成とは
\(\small{ \ \sin\theta+\sqrt{3}\cos\theta=2\sin\left(\theta+\displaystyle\frac{\pi}{3}\right) \ }\)のように\(\small{ \ \sin \ }\)と\(\small{ \ \cos \ }\)の和や差を\(\small{ \ \sin \ }\)だけ、または\(\small{ \ \cos \ }\)だけにまとめることを三角関数の合成っていうんだ。
\(\small{ \ \sin\theta \ }\)と\(\small{ \ \sqrt{3}\cos\theta \ }\)の\(\small{ \ 2 \ }\)つの関数が変化するけど、合成することで\(\small{ \ \sqrt{2}\sin\left(\theta+\displaystyle\frac{\pi}{4}\right) \ }\)ってなって、\(\small{ \ 1 \ }\)つの関数に変わるから色々求めやすくなりそうだよね。
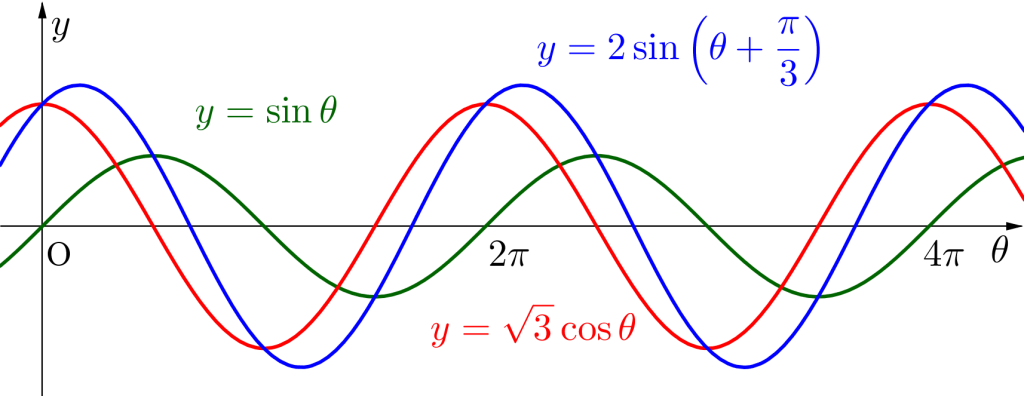
つまり三角関数の合成を利用することで、\(\small{ \ \sin\theta \ }\)と\(\small{ \ \cos\theta \ }\)の\(\small{ \ 2 \ }\)つの関数の和や差を\(\small{ \ 1 \ }\)つの関数にまとめることが出来るってメリットがあるんだ。
三角関数の合成できる形の確認
次にどんな形の三角関数が合成できるのか考えてみよう。
実はこれが一番重要だからね。
合成してって言われて合成することは出来ても、どの問題で合成しないといけないのかってことが分かってない人が多いからきちんと理解しよう。
合成できる形って決まってるからまずはそこを確認しておこう。
次の\(\small{ \ 5 \ }\)つの形を見てみよう。
①\(\small{ \ \sin\theta+\cos\theta \ }\)
②\(\small{ \ \sin\theta+\cos2\theta \ }\)
③\(\small{ \ 3\sin2\theta+5\cos2\theta \ }\)
④\(\small{ \ 2\sin2\theta+3\cos\theta \ }\)
⑤\(\small{ \ \sin\theta+\sin2\theta \ }\)
この①~⑤の中でどの形が合成できるかわかるかな?
合成できるのは①と③なんだ。
①と③に共通しているのは\(\small{ \ \sin \ }\)と\(\small{ \ \cos \ }\)の足し算(引き算も可)で偏角が同じ値であるってことなんだ。
それが満たされていれば\(\small{ \ \sin \ }\)と\(\small{ \ \cos \ }\)の係数が違っても構わない。
つまり合成できるのは\(\small{ \ a\sin\theta+b\cos\theta \ }\)や\(\small{ \ a\sin2\theta+b\cos2\theta \ }\)で、偏角が同じ\(\small{ \ \sin \ }\)と\(\small{ \ \cos \ }\)の足し算・引き算なんだ。
まずはこのことをきちんと覚えておこう。
合成できてもいつ使っていいかわからないじゃ意味ないからね。
三角関数の合成(sin型)
それじゃ合成のやり方について勉強していこう。
\(\small{ \ a\sin\theta+b\cos\theta=R\sin\left(\theta+\alpha\right) \ }\)に変形することを三角関数の合成っていうからね。
最初に\(\small{ \ \sin\theta \ }\)と\(\small{ \ \cos\theta \ }\)のそれぞれの係数の\(\small{ \ 2 \ }\)乗の和に根号をつけて式を括りだそう。
=\sqrt{a^2+b^2}\left(\displaystyle\frac{a}{\sqrt{a^2+b^2}}\sin\theta+\displaystyle\frac{b}{\sqrt{a^2+b^2}}\cos\theta\right) \ }\)
このとき括弧内の\(\small{ \ \sin\theta \ }\)と\(\small{ \ \cos\theta \ }\)の係数をそれぞれ\(\small{ \ 2 \ }\)乗して加えてみると
\(\small{ \ \left(\displaystyle\frac{a}{\sqrt{a^2+b^2}}\right)^2+\left(\displaystyle\frac{b}{\sqrt{a^2+b^2}}\right)^2\\[8pt]
=\displaystyle\frac{a^2}{a^2+b^2}+\displaystyle\frac{b^2}{a^2+b^2}\\[12pt]
=1 \ }\)
つまり係数を\(\small{ \ 2 \ }\)乗して足すと\(\small{ \ 1 \ }\)になることがわかったよね。
\(\small{ \ 2 \ }\)乗して足して\(\small{ \ 1 \ }\)にするために\(\small{ \ \sin\theta \ }\)と\(\small{ \ \cos\theta \ }\)のそれぞれの係数の\(\small{ \ 2 \ }\)乗の和に根号をつけて括りだしたんだ。
\(\small{ \ 2 \ }\)乗したものの和が\(\small{ \ 1 \ }\)になるって言ったら思いつくのが一つあるよね。
それは\(\small{ \ \sin\theta \ }\)と\(\small{ \ \cos\theta \ }\)。
でもすでに\(\small{ \ \theta \ }\)はすでに使ってるから別な値\(\small{ \ \alpha \ }\)を用いて
\(\small{ \ \displaystyle\frac{a}{\sqrt{a^2+b^2}}=\cos\alpha \ }\)\(\small{ \ \displaystyle\frac{b}{\sqrt{a^2+b^2}}=\sin\alpha \ }\)としよう。
当然\(\small{ \ \sin^2\alpha+\cos^2\alpha=1 \ }\)も成り立つよね。
\(\small{ \ \sin\theta \ }\)の係数が\(\small{ \ \cos\alpha \ }\)で、\(\small{ \ \cos\theta \ }\)の係数が\(\small{ \ \sin\alpha \ }\)ね。
すると
ってなるよね。
加法定理から\(\small{ \ \sin\left(\alpha+\beta\right)=\sin\alpha\cos\beta+\cos\alpha\sin\beta \ }\)だから
つまり\(\small{ \ a\sin\theta+b\cos\theta=R\sin\left(\theta+\alpha\right) \ }\)のとき
\(\small{ \ \begin{eqnarray}
\left\{
\begin{array}{l}
R=\sqrt{a^2+b^2}\\
\sin\alpha=\displaystyle\frac{b}{\sqrt{a^2+b^2}}\\
\cos\alpha=\displaystyle\frac{b}{\sqrt{a^2+b^2}}
\end{array}
\right.
\end{eqnarray} \ }\)
になるんだ。
ってことは\(\small{ \ a\sin\theta+b\cos\theta=\sqrt{a^2+b^2}\sin\left(\theta+\alpha\right) \ }\)の変形は、左辺→右辺は合成、右辺→左辺は加法定理ってことになるよね。
次の式を\(\small{ \ r\sin(\theta+\alpha) \ }\)の形に変形せよ。
(1)\(\small{ \ \sqrt{3}\sin\theta+\cos\theta \ }\)
(2)\(\small{ \ \sqrt{3}\sin\theta-3\cos\theta \ }\)
(1)
\(\small{\begin{eqnarray} \ &&\sqrt{3}\sin\theta+\cos\theta\\
&=&\sqrt{3+1}\left(\displaystyle\frac{\sqrt{3}}{2}\sin\theta+\displaystyle\frac{1}{2}\cos\theta\right) \ \end{eqnarray}}\)
\(\small{ \ \cos\alpha=\displaystyle\frac{\sqrt{3}}{2}, \ \sin\alpha=\displaystyle\frac{1}{2} \ }\)\(\small{ \ \therefore \alpha=\displaystyle\frac{\pi}{6} \ }\)
\(\small{\begin{eqnarray} \ &&\sqrt{3}\sin\theta+\cos\theta\\[3pt]
&=&2\left(\displaystyle\frac{\sqrt{3}}{2}\sin\theta+\displaystyle\frac{1}{2}\cos\theta\right)\\[5pt]
&=&2\left(\sin\theta\cos\displaystyle\frac{\pi}{6}+\cos\theta\sin\displaystyle\frac{\pi}{6}\right)\\[5pt]
&=&2\sin\left(\theta+\displaystyle\frac{\pi}{6}\right) \ \end{eqnarray}}\)
(2)
\(\small{\begin{eqnarray} \ &&\sqrt{3}\sin\theta-3\cos\theta\\
&=&\sqrt{3+9}\left(\displaystyle\frac{\sqrt{3}}{2\sqrt{3}}\sin\theta-\displaystyle\frac{3}{2\sqrt{3}}\cos\theta\right)\\
&=&2\sqrt{3}\left(\displaystyle\frac{1}{2}\sin\theta-\displaystyle\frac{\sqrt{3}}{2}\cos\theta\right) \ \end{eqnarray}}\)
\(\small{ \ \cos\alpha=\displaystyle\frac{1}{2}, \ \sin\alpha=\displaystyle\frac{\sqrt{3}}{2} \ }\)\(\small{ \ \therefore \alpha=\displaystyle\frac{\pi}{3} \ }\)
\(\small{\begin{eqnarray} \ &&\sqrt{3}\sin\theta-3\cos\theta\\[5pt]
&=&2\sqrt{3}\left(\displaystyle\frac{1}{2}\sin\theta-\displaystyle\frac{\sqrt{3}}{2}\cos\theta\right)\\[5pt]
&=&2\sqrt{3}\left(\sin\theta\cos\displaystyle\frac{\pi}{3}-\cos\theta\sin\displaystyle\frac{\pi}{3}\right)\\[5pt]
&=&2\sqrt{3}\sin\left(\theta-\displaystyle\frac{\pi}{3}\right) \ \end{eqnarray}}\)

つまり\(\small{ \ 2\sqrt{3}\sin\left(\theta+\displaystyle\frac{5}{3}\pi\right) \ }\)になって上の答えとちょうど\(\small{ \ 2\pi \ }\)ずれて同じ値になっているのが分かるよね。
三角関数の合成(cos型)
三角関数の合成って言ったら、\(\small{ \ a\sin\theta+b\cos\theta=R\sin\left(\theta+\alpha\right) \ }\)に変形することって学校で教わると思うけど、入試では\(\small{ \ R\cos\left(\theta+\alpha\right) \ }\)って合成することもあるから、この変形も確認しておこう。
\(\small{ \ \cos \ }\)の合成を教えてくれない学校の先生も多いからね。
式の変形の途中までは\(\small{ \ \sin \ }\)型のときと同じなんだけど、最後に加法定理を利用する部分で\(\small{ \ \sin\theta \ }\)の係数を\(\small{ \ \sin\alpha \ }\)に、\(\small{ \ \cos\theta \ }\)の係数を\(\small{ \ \cos\alpha \ }\)にするんだ。
これで\(\small{ \ \cos \ }\)型に合成することが出来たよね。
次の式を\(\small{ \ r\cos(\theta+\alpha) \ }\)の形に変形せよ。
(1)\(\small{ \ \sqrt{3}\sin\theta+\cos\theta \ }\)
(2)\(\small{ \ \sqrt{3}\sin\theta-3\cos\theta \ }\)
(1)
\(\small{\begin{eqnarray} \ &&\sqrt{3}\sin\theta+\cos\theta\\[5pt]
&=&\sqrt{3+1}\left(\displaystyle\frac{\sqrt{3}}{2}\sin\theta+\displaystyle\frac{1}{2}\cos\theta\right) \ \end{eqnarray}}\)
\(\small{ \ \sin\alpha=\displaystyle\frac{\sqrt{3}}{2}, \ \cos\alpha=\displaystyle\frac{1}{2} \ }\)\(\small{ \ \therefore \alpha=\displaystyle\frac{\pi}{3} \ }\)
\(\small{\begin{eqnarray} \ &&\sqrt{3}\sin\theta+\cos\theta\\[5pt]
&=&2\left(\sin\theta\sin\displaystyle\frac{\pi}{3}+\cos\theta\cos\displaystyle\frac{\pi}{3}\right)\\[5pt]
&=&2\cos\left(\theta-\displaystyle\frac{\pi}{3}\right) \ \end{eqnarray}}\)
(2)
\(\small{\begin{eqnarray} \ &&\sqrt{3}\sin\theta-3\cos\theta\\
&=&\sqrt{3+9}\left(\displaystyle\frac{\sqrt{3}}{2\sqrt{3}}\sin\theta-\displaystyle\frac{3}{2\sqrt{3}}\cos\theta\right)\\
&=&2\sqrt{3}\left(\displaystyle\frac{1}{2}\sin\theta-\displaystyle\frac{\sqrt{3}}{2}\cos\theta\right) \ \end{eqnarray}}\)
\(\small{ \ \sin\alpha=\displaystyle\frac{1}{2}, \ \cos\alpha=-\displaystyle\frac{\sqrt{3}}{2} \ }\)\(\small{ \ \therefore \alpha=\displaystyle\frac{5}{6}\pi \ }\)
\(\small{\begin{eqnarray} \ &&\sqrt{3}\sin\theta-3\cos\theta\\
&=&2\sqrt{3}\left(\sin\theta\sin\displaystyle\frac{5}{6}\pi+\cos\theta\cos\displaystyle\frac{5}{6}\pi\right)\\[5pt]
&=&2\sqrt{3}\cos\left(\theta-\displaystyle\frac{5}{6}\pi\right) \ \end{eqnarray}}\)

この問題の場合\(\small{ \ \cos\left(\theta-\alpha\right) \ }\)を利用したから\(\small{ \ \sin\alpha=\displaystyle\frac{1}{2}, \ \cos\alpha=-\displaystyle\frac{\sqrt{3}}{2} \ }\)ってしたけど、\(\small{ \ \cos\left(\theta+\alpha\right) \ }\)を利用したら\(\small{ \ \sin\alpha=-\displaystyle\frac{1}{2}, \ \cos\alpha=-\displaystyle\frac{\sqrt{3}}{2} \ }\)になって
\(\small{ \ 2\sqrt{3}\cos\left(\theta+\displaystyle\frac{7}{6}\pi\right) \ }\)になるからね。
上の答えとちょうど\(\small{ \ 2\pi \ }\)ずれてるのが分かるよね。つまり同じ値になるってことだからね。
図形を利用した合成
今度は図形を利用した合成を考えてみよう。
\(\small{ \ a\sin\theta+b\cos\theta \ }\)を合成する場合、図のように\(\small{ \ (x, \ y)=(a, \ b) \ }\)をとり、その偏角を\(\small{ \ \alpha \ }\)に設定するんだ。
このとき注意しないといけないのが\(\small{ \ \sin\theta \ }\)の係数が\(\small{ \ x \ }\)座標で、\(\small{ \ \cos\theta \ }\)の係数が\(\small{ \ y \ }\)座標になること。逆にすると全然違う答えになるから間違えないようにね。
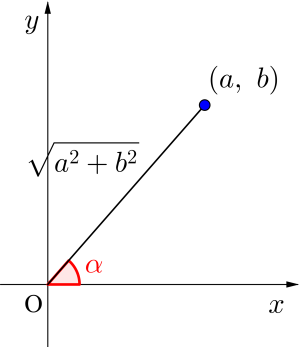
このとき
\(\small{ \ \cos\alpha=\displaystyle\frac{a}{\sqrt{a^2+b^2}}, \ \sin\alpha=\displaystyle\frac{b}{\sqrt{a^2+b^2}} \ }\)になるから
=\sqrt{a^2+b^2}\left(\displaystyle\frac{a}{\sqrt{a^2+b^2}}\sin\theta+\displaystyle\frac{b}{\sqrt{a^2+b^2}}\cos\theta\right)\\[5pt] =\sqrt{a^2+b^2}\left(\sin\theta\cos\alpha+\cos\theta\sin\alpha\right)\\[3pt] =\sqrt{a^2+b^2}\sin\left(\theta+\alpha\right) \ }\)
つまり図から\(\small{ \ \sqrt{a^2+b^2} \ }\)と\(\small{ \ \alpha \ }\)が求まれば、\(\small{ \ a\sin\theta+b\cos\theta=\sqrt{a^2+b^2}\sin\left(\theta+\alpha\right) \ }\)って簡単に合成できるよね。

でもほとんどの問題が\(\small{ \ \sin \ }\)型の問題だから、この方法だと素早く合成できるよね。だから学校の先生もこの方法を教える先生が多いんだ。
この方法をマスターして少しでも早く合成できるようにしておこう。
でも\(\small{ \ \cos \ }\)型の合成も入試では必要になるかもしれないから、加法定理を利用して合成する方法も確実に押さえておこう。
有名角とその他の角の合成
次は合成したときの\(\small{ \ r\sin\left(\theta+\alpha\right) \ }\)の\(\small{ \ \alpha \ }\)について考えてみよう。
\(\small{ \ \alpha \ }\)が有名角になるためには、\(\small{ \ a\sin\theta+b\cos\theta \ }\)の係数\(\small{ \ a, \ b \ }\)に条件があるんだ。
\(\small{ \ \sin\alpha=\displaystyle\frac{b}{\sqrt{a^2+b^2}} \ }\)に\(\small{ \ \cos\alpha=\displaystyle\frac{b}{\sqrt{a^2+b^2}} \ }\)なるから\(\small{ \ \sin\alpha :\cos\alpha=a:b \ }\)って言える。
つまりこの\(\small{ \ a:b \ }\)が有名角の\(\small{ \ \sin \ }\)と\(\small{ \ \cos \ }\)の比なら\(\small{ \ \alpha \ }\)が有名角になるんだ。
有名角の三角関数の比は\(\small{ \ \pm \ }\)の符号を無視すると\(\small{ \ \sqrt{3}:1, \ 1:1, \ 1:\sqrt{3} \ }\)のどれかになるから、\(\small{ \ a\sin\theta+b\cos\theta \ }\)の係数\(\small{ \ a, \ b \ }\)が\(\small{ \ \sqrt{3}:1, \ 1:1, \ 1:\sqrt{3} \ }\)の比になっていれば、合成したときの\(\small{ \ \alpha \ }\)が有名角になるんだ。
じゃあ有名角にならない場合は合成できないのかっていうとそんなことはない。
ただ有名角にならないから角について補足を書いておかないといけないんだ。
\(\small{ \ 3\sin\theta+4\cos\theta \ }\)を合成してみよう。
\(\small{ \ 3\sin\theta+4\cos\alpha\\
=\sqrt{3^2+4^2}\left(\displaystyle\frac{3}{5}\sin\theta+\displaystyle\frac{4}{5}\cos\theta\right)\\
=5\sin\left(\theta+\alpha\right) \ }\)
ただし、\(\small{ \ \alpha \ }\)は\(\small{ \ \sin\alpha=\displaystyle\frac{4}{5} \ }\)、\(\small{ \ \cos\alpha=\displaystyle\frac{3}{5} \ }\)を満たす角
このように\(\small{ \ \alpha \ }\)は有名角じゃないから値を答えられないけど\(\small{ \ \sin\alpha \ }\)と\(\small{ \ \cos\alpha \ }\)の値を書いておけば\(\small{ \ \alpha \ }\)がどんな角かってことはわかるよね。
だから\(\small{ \ \alpha \ }\)が有名角にならないからといって合成できないわけじゃないからね。

Point 三角関数の合成
①加法定理を利用した合成をマスターしよう
②図形を利用した\(\small{ \ \sin \ }\)型の合成をマスターしよう
\(\small{ \ t \ }\)の関数\(\small{ \ g(t)=A\sin\left(t-\alpha\right)+B\sin\left(t+\alpha\right) \ }\)を考える。ただし、\(\small{ \ A, \ B, \ \alpha \ }\)は実数で、\(\small{ \ A\gt B \gt0 \ }\)とする。
(1)\(\small{ \ g(t) \ }\)を\(\small{ \ C\sin t+D\cos t \ }\)の形に変形し、\(\small{ \ C \ }\)と\(\small{ \ D \ }\)を求めよ。
(2)\(\small{ \ g(t) \ }\)を\(\small{ \ F\sin \left(t+\beta\right) \ }\)の形に変形し、このときの\(\small{ \ F \ }\)を求め、\(\small{ \ \beta\ }\)が満たすべき条件示せ。ただし、\(\small{ \ F\gt0 \ }\)とする。
(3)\(\small{ \ \alpha \ }\)が\(\small{ \ 0\leqq \alpha \lt \pi \ }\)の範囲で変化するとき、\(\small{ \ F \ }\)の最大値と最小値とそれらを与える\(\small{ \ \alpha \ }\)の値を求めよ。
(1)
&=&A\left(\sin t \cos\alpha-\cos t \sin\alpha\right)+B\left(\sin t \cos\alpha+\cos t \sin\alpha\right)\\
&=&\left(A+B\right)\cos\alpha\sin t+\left(-A+B\right)\sin\alpha\cos t \ \end{eqnarray}}\)
\(\small{ \ \therefore \begin{eqnarray}
\left\{
\begin{array}{l}
C=\left(A+B\right)\cos\alpha\\
D=\left(-A+B\right)\sin\alpha
\end{array}
\right.
\end{eqnarray} \ }\)
(2)
(1)の結果より
\(\small{\begin{eqnarray} \ g(t)&=&C\sin t+D\cos t\\
&=&\sqrt{C^2+D^2}\sin\left(t+\beta\right) \ \end{eqnarray}}\)
ただし\(\small{ \ \beta \ }\)は\(\small{ \ \left(C, \ D\right) \ }\)の偏角である。
&=&A^2+B^2+2AB\cos2\alpha \ \end{eqnarray}}\)
\(\small{ \ \therefore F=\sqrt{A^2+B^2+2AB\cos2\alpha} \ }\)
\(\small{ \ \beta \ }\)の満たすべき条件は
\(\small{\begin{eqnarray} \ \sin\beta&=&\displaystyle\frac{\left(-A+B\right)\sin\alpha}{\sqrt{A^2+B^2+2AB\cos2\alpha}}\\
\cos\beta&=&\displaystyle\frac{\left(A+B\right)\cos\alpha}{\sqrt{A^2+B^2+2AB\cos2\alpha}}\ \end{eqnarray}}\)
(3)
\(\small{ \ 0\leqq \alpha \lt \pi \ }\)より\(\small{ \ 0\leqq 2\alpha \lt \pi \ }\)
\(\small{ \ A\gt B\gt 0 \ }\)より
\(\small{ \ F \ }\)が最大のとき\(\small{ \ \cos2\alpha=1 \ }\)
\(\small{ \ F \ }\)が最小のとき\(\small{ \ \cos2\alpha=-1 \ }\)
\(\small{ \ \begin{eqnarray}
\left\{
\begin{array}{l}
\mathrm{max}F=A+B \ (\alpha=0)\\
\mathrm{min}F=A-B \ \left(\alpha=\displaystyle\frac{\pi}{2}\right)
\end{array}
\right.
\end{eqnarray} \ }\)

