こんにちは、リンス(@Lins016)です。
今回は三角関数を含む不等式・三角不等式について学習していこう。
三角不等式
三角不等式っていうと『 \(\small{ \ |x+y|\leqq |x|+|y| \ }\)っていう有名不等式』のことを表す場合と『三角関数を含む不等式』のことを表す場合がある。今回は三角関数を含む不等式の\(\small{ \ \theta \ }\)の範囲を求める不等式について考えていこう。
図形と計量でも不等式について学習したけど、今回は角度の部分が\(\small{ \ \theta \ }\)の一次式の問題になるから、まずは基本的な不等式の解き方を以前の記事でチェックしておこう。
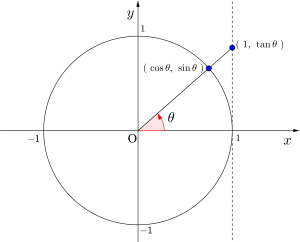
・\(\small{ \ \sin \ }\)の不等式:
動径と単位円の交点の\(\small{ \ y \ }\)座標
・\(\small{ \ \cos \ }\)の不等式:
動径と単位円の交点の\(\small{ \ x \ }\)座標
・\(\small{ \ \tan \ }\)の不等式:
動径と原点を結ぶ直線と\(\small{ \ x=1 \ }\)との交点の\(\small{ \ y \ }\)座標
三角関数を含む不等式
不等式の場合は単位円を利用して問題を解こう。
\(\small{ \ \theta \ }\)の一次式を\(\small{ \ t \ }\)と置換して、まずは\(\small{ \ \theta \ }\)の定義域から\(\small{ \ t \ }\)の範囲を求めよう。
\(\small{ \ t \ }\)の範囲を求めたら、不等式を満たす角度を求めよう。
そのとき単位円で見るべきところは、式が\(\small{ \ \sin\theta \ }\)なら動径と単位円の交点の\(\small{ \ y \ }\)座標、\(\small{ \ \cos\theta \ }\)なら\(\small{ \ x \ }\)座標、\(\small{ \ \tan\theta \ }\)なら動径の延長と\(\small{ \ x=1 \ }\)の交点の\(\small{ \ y \ }\)座標になるからね。
条件を満たす動径の範囲を確認して、\(\small{ \ t \ }\)の範囲から\(\small{ \ \theta \ }\)の範囲に戻そう。
\(\small{ \ 0\leqq \theta \lt 2\pi \ }\)のとき、次の不等式を解け。
\(\small{ \ \sin\left(2\theta+\displaystyle \frac{\pi}{3}\right)\geqq \displaystyle\frac{\sqrt{2}}{2} \ }\)
\(\small{ \ \sin\left(2\theta+\displaystyle \frac{\pi}{3}\right)\geqq \displaystyle \frac{\sqrt{2}}{2} \ }\)
\(\small{ \ t=2\theta+\displaystyle \frac{\pi}{3} \ }\)とすると\(\small{ \ 0\leqq \theta \lt 2\pi \ }\)より
\(\small{ \ \displaystyle \frac{\pi}{3}\leqq t \lt \displaystyle \frac{13}{3}\pi \ }\)
\(\small{ \ \sin t \geqq \displaystyle \frac{\sqrt{2}}{2} \ }\)の解は
\(\small{\begin{eqnarray}
\left\{
\begin{array}{l}\displaystyle \frac{\pi}{3} \leqq t \leqq \displaystyle \frac{3}{4}\pi\\[3pt]
\displaystyle \frac{9}{4}\pi \leqq t \leqq \displaystyle \frac{11}{4}\pi\\[3pt]
\displaystyle \frac{17}{4}\pi \leqq t \lt\displaystyle \frac{13}{3}\pi
\end{array}
\right.
\end{eqnarray} \ }\)
\(\small{ \ t=2\theta+\displaystyle \frac{\pi}{3} \ }\)より
\(\small{\begin{eqnarray}
\left\{
\begin{array}{l}0 \leqq \theta \leqq \displaystyle \frac{5}{24}\pi\\[3pt]
\displaystyle \frac{23}{24}\pi \leqq \theta \leqq \displaystyle \frac{29}{24}\pi\\[3pt]
\displaystyle \frac{47}{24}\pi \leqq \theta \lt 2\pi
\end{array}
\right.
\end{eqnarray} \ }\)
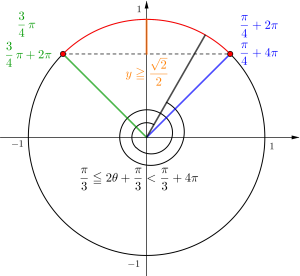

\(\small{ \ t \ }\)の解で\(\small{ \ \displaystyle \frac{9}{4}\pi \ }\)、\(\small{ \ \displaystyle \frac{11}{4}\pi \ }\)、\(\small{ \ \displaystyle \frac{17}{4}\pi \ }\)が出てくるけどこれは、\(\small{ \ \displaystyle \frac{9}{4}\pi=\displaystyle \frac{\pi}{4}+2\pi \ }\)、\(\small{ \ \displaystyle \frac{11}{4}\pi=\displaystyle\frac{3}{4}\pi+2\pi \ }\)、\(\small{ \ \displaystyle \frac{17}{4}\pi=\displaystyle \frac{\pi}{4}+4\pi \ }\)って動径の位置に\(\small{ \ 2\pi \ }\)ずつ足した値だからね。
三角関数を含む不等式と一般解
次に上の例題\(\small{ \ 0\leqq \theta \lt 2\pi \ }\)のとき、\(\small{ \ \sin\left(2\theta+\displaystyle \frac{\pi}{3}\right)\geqq \displaystyle \frac{\sqrt{2}}{2} \ }\)を一般解を利用して考えてみよう。
\(\small{ \ \sin\left(2\theta+\displaystyle \frac{\pi}{3}\right)\geqq \displaystyle \frac{\sqrt{2}}{2} \ }\)より\(\small{ \ \displaystyle \frac{\pi}{4}+2n\pi \leqq 2\theta+\displaystyle \frac{\pi}{3}\leqq \displaystyle \frac{3}{4}\pi+2n\pi \ }\)
\(\small{ \ -\displaystyle \frac{\pi}{12}+2n\pi \leqq 2\theta \leqq \displaystyle \frac{5}{12}\pi+2n\pi \ }\)
\(\small{ \ \therefore -\displaystyle \frac{\pi}{24}+n\pi \leqq \theta \leqq \displaystyle \frac{5}{24}\pi+n\pi \ }\)
\(\small{ \ 0\leqq \theta \lt 2\pi \ }\)を満たす\(\small{ \ \theta \ }\)は
\(\small{\begin{eqnarray}
\left\{
\begin{array}{l}0 \leqq \theta \leqq \displaystyle \frac{5}{24}\pi\\[3pt]
\displaystyle \frac{23}{24}\pi \leqq \theta \leqq \displaystyle \frac{29}{24}\pi\\[3pt]
\displaystyle \frac{47}{24}\pi \leqq \theta \lt 2\pi
\end{array}
\right.
\end{eqnarray} \ }\)
上の答えを見てわかるけど、求めた一般解\(\small{ \ -\displaystyle \frac{\pi}{24}+n\pi \leqq \theta \leqq \displaystyle \frac{5}{24}\pi+n\pi \ }\)の\(\small{ \ n \ }\)にただ整数を代入するだけじゃダメなんだ。
グラフを見てもらえばわかるけど、グラフの両端が\(\small{ \ y=\displaystyle\frac{\sqrt{2}}{2} \ }\)との交点になってないよね。
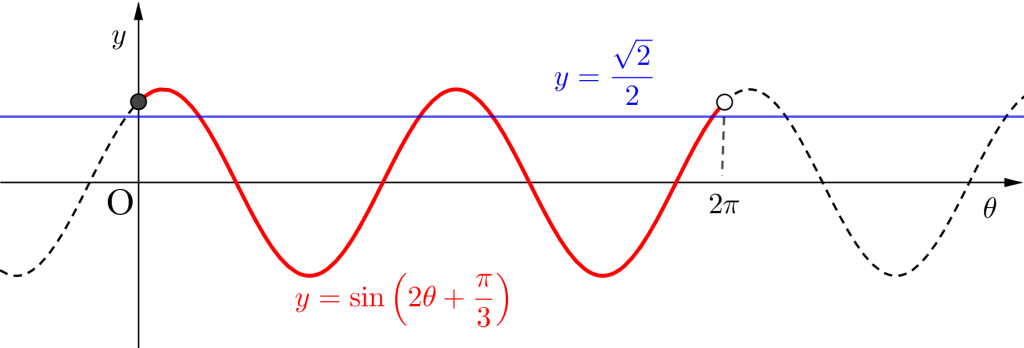
\(\small{ \ n \ }\)に整数を代入した値は\(\small{ \ y=\sin\left(2\theta+\displaystyle \frac{\pi}{3}\right) \ }\)と\(\small{ \ y=\displaystyle\frac{\sqrt{2}}{2} \ }\)との交点になるから、その値が定義域の両端と綺麗に重なっているとは限らないんだ。
だから\(\small{ \ n \ }\)に整数を代入して定義域の範囲を満たす部分を考えよう。
\(\small{ \ 0\leqq \theta \lt 2\pi \ }\)のとき、次の不等式を解け。
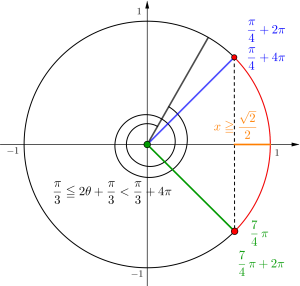
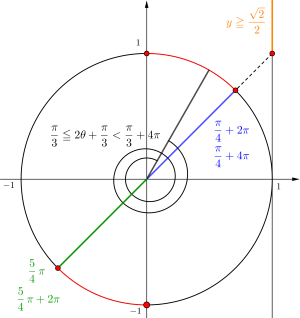
(1)\(\small{ \ \cos\left(2\theta+\displaystyle \frac{\pi}{3}\right)\geqq \displaystyle \frac{\sqrt{2}}{2} \ }\)
(2)\(\small{ \ \tan\left(2\theta+\displaystyle \frac{\pi}{3}\right)\geqq1 \ }\)
(1)\(\small{ \ \cos\left(2\theta+\displaystyle \frac{\pi}{3}\right)\geqq \displaystyle \frac{\sqrt{2}}{2} \ }\)
\(\small{ \ t=2\theta+\displaystyle \frac{\pi}{3} \ }\)とすると\(\small{ \ 0\leqq \theta \lt 2\pi \ }\)より
\(\small{ \ \displaystyle \frac{\pi}{3}\leqq t \lt \displaystyle \frac{13}{3}\pi \ }\)
\(\small{ \ \cos t \geqq \displaystyle \frac{\sqrt{2}}{2} \ }\)の解は
\(\small{\begin{eqnarray}
\left\{
\begin{array}{l}\displaystyle \frac{7}{4}\pi \leqq t \leqq \displaystyle \frac{9}{4}\pi\\[3pt]
\displaystyle \frac{15}{4}\pi \leqq t \leqq \displaystyle \frac{17}{4}\pi
\end{array}
\right.
\end{eqnarray} \ }\)
\(\small{ \ t=2\theta+\displaystyle \frac{\pi}{3} \ }\)より
\(\small{\begin{eqnarray}
\left\{
\begin{array}{l}\displaystyle \frac{17}{24}\pi \leqq \theta \leqq \displaystyle \frac{23}{24}\pi\\[3pt]
\displaystyle \frac{41}{24}\pi \leqq \theta \leqq \displaystyle \frac{47}{24}\pi
\end{array}
\right.
\end{eqnarray} \ }\)
(2)\(\small{ \ \tan\left(2\theta+\displaystyle \frac{\pi}{3}\right)\geqq1 \ }\)
\(\small{ \ t=2\theta+\displaystyle \frac{\pi}{3} \ }\)とすると\(\small{ \ 0\leqq \theta \lt 2\pi \ }\)より
\(\small{ \ \displaystyle \frac{\pi}{3}\leqq t \lt \displaystyle \frac{13}{3}\pi \ }\)
\(\small{ \ \tan t \geqq 1 \ }\)の解は
\(\small{\begin{eqnarray}
\left\{
\begin{array}{l}\displaystyle \frac{\pi}{3}\leqq t \lt \displaystyle \frac{\pi}{2}\\[3pt]
\displaystyle \frac{5}{4}\pi\leqq t \lt \displaystyle \frac{3}{2}\pi\\[3pt]
\displaystyle \frac{9}{4}\pi \leqq t \lt \displaystyle \frac{5}{2}\pi\\[3pt]
\displaystyle \frac{13}{4}\pi \leqq t \lt \displaystyle \frac{7}{2}\pi\\[3pt]
\displaystyle \frac{17}{4}\pi \leqq t \lt \displaystyle \frac{13}{3}\pi
\end{array}
\right.
\end{eqnarray} \ }\)
\(\small{ \ t=2\theta+\displaystyle \frac{\pi}{3} \ }\)より
\(\small{\begin{eqnarray}
\left\{
\begin{array}{l}0\leqq \theta \lt\displaystyle\frac{\pi}{12}\\[3pt]
\displaystyle\frac{5}{12}\pi \leqq \theta \lt \displaystyle\frac{7}{12}\pi\\[3pt]
\displaystyle\frac{11}{12}\pi \leqq \theta \lt \displaystyle\frac{13}{12}\pi\\[3pt]
\displaystyle\frac{17}{12}\pi \leqq \theta \lt \displaystyle\frac{19}{12}\pi\\[3pt]
\displaystyle\frac{23}{12}\pi \leqq \theta \lt 2\pi
\end{array}
\right.
\end{eqnarray} \ }\)
\(\small{ \ \cos\left(2\theta+\displaystyle \frac{\pi}{3}\right)\geqq \displaystyle \frac{\sqrt{2}}{2} \ }\)
この不等式の一般解は\(\small{ \ -\displaystyle \frac{\pi}{4}+2n\pi \leqq 2\theta+\displaystyle \frac{\pi}{3}\leqq \displaystyle \frac{\pi}{4}+2n\pi \ }\)
\(\small{ \ -\displaystyle \frac{7}{12}\pi+2n\pi\leqq 2\theta \leqq -\displaystyle \frac{\pi}{12}+2n\pi \ }\)
\(\small{ \ \therefore -\displaystyle \frac{7}{24}\pi+n\pi\leqq \theta \leqq -\displaystyle \frac{\pi}{24}+n\pi \ }\)
よって\(\small{ \ 0\leqq \theta \lt 2\pi \ }\)を満たす\(\small{ \ \theta \ }\)は
\(\small{\begin{eqnarray}
\left\{
\begin{array}{l}\displaystyle \frac{17}{24}\pi \leqq \theta \leqq \displaystyle \frac{23}{24}\pi\\[3pt]
\displaystyle \frac{41}{24}\pi \leqq \theta \leqq \displaystyle \frac{47}{24}\pi
\end{array}
\right.
\end{eqnarray} \ }\)
(2)\(\small{ \ \tan\left(2\theta+\displaystyle \frac{\pi}{3}\right)\geqq1 \ }\)
この不等式の一般解は
\(\small{ \ \displaystyle\frac{\pi}{4}+n\pi\leqq 2\theta+\displaystyle\frac{\pi}{3}\lt \displaystyle\frac{\pi}{2}+n\pi \ }\)
\(\small{ \ -\displaystyle\frac{\pi}{12}+n\pi\leqq 2\theta\lt \displaystyle\frac{\pi}{6}+n\pi \ }\)
\(\small{ \ \therefore -\displaystyle\frac{\pi}{24}+\displaystyle\frac{n}{2}\pi\leqq \theta\lt \displaystyle\frac{\pi}{12}+\displaystyle\frac{n}{2}\pi \ }\)
\(\small{ \ 0\leqq \theta \lt 2\pi \ }\)を満たすのは
\(\small{\begin{eqnarray}
\left\{
\begin{array}{l}0\leqq \theta \lt\displaystyle\frac{\pi}{12}\\[3pt]
\displaystyle\frac{5}{12}\pi \leqq \theta \lt \displaystyle\frac{7}{12}\pi\\[3pt]
\displaystyle\frac{11}{12}\pi \leqq \theta \lt \displaystyle\frac{13}{12}\pi\\[3pt]
\displaystyle\frac{17}{12}\pi \leqq \theta \lt \displaystyle\frac{19}{12}\pi\\[3pt]
\displaystyle\frac{23}{12}\pi \leqq \theta \lt 2\pi
\end{array}
\right.
\end{eqnarray} \ }\)

つまり\(\small{ \ \sin \ }\)や\(\small{ \ \cos \ }\)なら周期が\(\small{ \ 2\pi \ }\)だから動径の位置に\(\small{ \ 2\pi \ }\)ずつ足せばいいし、\(\small{ \ \tan \ }\)なら周期は\(\small{ \ \pi \ }\)になるから\(\small{ \ \pi \ }\)ずつ足せばいいんだ。
Point 三角関数を含む不等式(三角不等式)
①\(\small{ \ \theta \ }\)の一次式を\(\small{ \ t \ }\)と置換して範囲を確認して解を求める
②一般解を利用する場合、定義域に注意

