こんにちは、リンス(@Lins016)です。
今回は対数関数の最大値・最小値について学習していこう。
対数関数の最大最小
対数関数の最大最小問題も大きく分けて2つあるんだ。
それは
①\(\small{ \ y=\log_{a}f(x) \ }\)のとき\(\small{ \ f(x) \ }\)の最大最小を考えるパターン
②\(\small{ \ \log_ax=t \ }\)と置換して\(\small{ \ t \ }\)の関数の最大最小を考えるパターン
この\(\small{ \ 2 \ }\)つに分けられる。
①は底の大きさに注意が必要で、②は\(\small{ \ t \ }\)の範囲に注意になる。
①真数の最大最小を考える
\(\small{ \ \begin{eqnarray}y&=&\log_2x+\log_2(4-x)\\
&=&\log_2x(4-x)\\
&=&\log2\left\{-(x-2)^2+4\right\}\end{eqnarray} \ }\)
②置換して\(\small{ \ t \ }\)の関数の最大最小を考える
\(\small{ \ \begin{eqnarray}y&=&(\log_{2}x)^2-\log_2x^2+3\\
&=&(\log_{2}x)^2-2\log_2x+3\\
&=&t^2-2t+3\\
&=&(t-1)^2+2\end{eqnarray} \ }\)
真数の最大最小と対数関数の最大最小
まずは\(\small{ \ y=\log_af(x) \ }\)の最大最小から考えていこう。
この形の問題は\(\small{ \ y=\log_2x+\log_2(4-x) \ }\)のような問題で\(\small{ \ y=\log_2x(4-x) \ }\)のように複数の対数を一つの対数にまとめ、かつ真数が\(\small{ \ x \ }\)の関数で表すことができる形。
この最大値と最小値を考える前にまずは\(\small{ \ y=\log_ax \ }\)のグラフをきちんと理解しておく必要がある。
\(\small{ \ y=\log_ax \ }\)は底が\(\small{ \ 1 \ }\)より大きいとき単調増加の関数で、底が\(\small{ \ 0\lt a \lt 1 \ }\)なら単調減少のグラフになる。
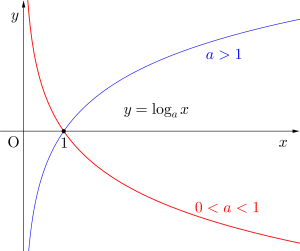
この基本的なグラフの形がわかっていない人は下の記事をもう一度チェックしておこう。
つまり\(\small{ \ y=\log_f(x) \ }\)の最大値・最小値を考えるとき\(\small{ \ f(x) \ }\)の最大値・最小値を考えればいいんだけど、底の大きさによって答えが変わってくるんだ。
\(\small{ \ f(x) \ }\)が最大値をとるとき
\(\small{ \ a\gt1 \ }\)なら\(\small{ \ y \ }\)も最大
\(\small{ \ 0\lt a\lt1 \ }\)なら\(\small{ \ y \ }\)は最小になる。
逆に\(\small{ \ f(x) \ }\)が最小値をとるとき
\(\small{ \ a\gt1 \ }\)なら\(\small{ \ y \ }\)も最小
\(\small{ \ 0\lt a\lt1 \ }\)なら\(\small{ \ y \ }\)は最大になる。
だから必ず底の大きさに注意して答えを出そう。
次の関数の最大値または最小値を求めよ。
(1)\(\small{ \ \log_3(2x-x^2) \ }\)
(2)\(\small{ \ \log_{\frac{1}{3}}(2x-x^2) \ }\)
(3)\(\small{ \ x\gt0, \ y\gt0, \ x+2y=8 \ }\)のとき\(\small{ \ \log_{10}x+\log_{10}y \ }\)
(1)\(\small{ \ \log_3(2x-x^2) \ }\)
\(\small{ \ =\log_3\left\{-(x-1)^2+1\right\} \ }\)
底\(\small{\gt1 \ }\)より
\(\small{ \ x=1 \ }\)のとき最大値\(\small{ \ 0 \ }\)
最小値なし
(2)\(\small{ \ \log_{\frac{1}{3}}(2x-x^2) \ }\)
\(\small{ \ =\log_{\frac{1}{3}}\left\{-(x-1)^2+1\right\} \ }\)
底\(\small{\lt1 \ }\)より
\(\small{ \ x=1 \ }\)のとき最小値\(\small{ \ 0 \ }\)
最大値なし
(3)\(\small{ \ \log_{10}x+\log_{10}y=\log_{10}xy \ }\)
\(\small{ \ x=8-2y \ }\)
\(\small{ \ 8-2y\gt0 \ }\)かつ\(\small{ \ y\gt0 \ }\)より\(\small{ \ 0\lt y \lt 4 \ }\)
\(\small{\begin{eqnarray} \ xy&=&(8-2y)y\\
&=&-2y^2+8y\\
&=&-2(y-2)^2+8 \ \end{eqnarray}}\)
底\(\small{\lt1 \ }\)より
\(\small{ \ (x, \ y)=(4, \ 2) \ }\)のとき最大値\(\small{ \ \log_28=3 \ }\)

対数関数を置換する最大値・最小値
次に対数関数を置換して二次関数や三次関数に変形する形の問題を見ていこう。
\(\small{ \ \left(\log_2x\right)^2 \ }\)のようにカッコの\(\small{ \ 2 \ }\)乗(または\(\small{ \ 3 \ }\)乗)があれば、このパターンになる。
括弧内の対数を\(\small{ \ t \ }\)とおいて考えていこう。
対数と対数の足し算や引き算は対数の性質から変形できるけど、対数と対数の掛け算はこれ以上変形することができないんだ。
\(\small{ \ \log_aM+\log_aN=\log_aMN \ }\)
\(\small{ \ \log_aM-\log_aN=\log_a\displaystyle \frac{M}{N} \ }\)
\(\small{ \ (\log_aM)(\log_aN)=?? \ }\)
だから対数の掛け算、つまり「対数の\(\small{ \ 2 \ }\)乗」はこれ以上変形できないから対数を\(\small{ \ t \ }\)と置換して問題を解いていこう。
この置換する問題の場合、置換した文字の範囲に注意しよう。\(\small{ \ t=\log_{a}x \ }\)のとき\(\small{ \ x\ }\)は真数だから\(\small{ \ x\gt0 \ }\)だけど、\(\small{ \ t \ }\)は全ての実数をとるから注意しよう。対数関数のグラフから明らかだよね。
よく勘違いして\(\small{ \ t \ }\)は対数だから正ってする人いるけど、そんなことないからね。
次の関数の最大値または最小値を求めよ。
(1)\(\small{ \ y=\left(\log_3x\right)^2+\log_39x^2 \ }\)
(2)\(\small{ \ y=\left(\log_2\displaystyle \frac{x}{2}\right)\left(\log_2\displaystyle \frac{x}{8}\right) \ \left(\displaystyle \frac{1}{2}\leqq x \leqq 8\right) \ }\)
(3)\(\small{ \ x\geqq2, \ y\geqq2, \ xy=16 \ }\)のとき\(\small{ \ \left(\log_{2}x\right)\left(\log_{2}y\right) \ }\)
(1)\(\small{ \ t=\log_3x \ }\)とすると
\(\small{\begin{eqnarray} \ y&=&\left(\log_3x\right)^2+\log_39x^2\\
&=&\left(\log_3x\right)^2+2\log_3x+2\\
&=&t^2+2t+2\\
&=&(t+1)^2+1 \ \end{eqnarray}}\)
\(\small{ \ t \ }\)はすべての実数をとるので
\(\small{ \ t=-1 \ }\)すなわち\(\small{ \ x=\displaystyle \frac{1}{3} \ }\)のとき最小値\(\small{ \ 1 \ }\)
最大値なし
(2)\(\small{ \ t=\log_2x \ }\)とすると\(\small{ \ \displaystyle \frac{1}{2}\leqq x \leqq 8 \ }\)より\(\small{ \ -1\leqq t \leqq 3 \ }\)
\(\small{\begin{eqnarray} \ y&=&\left(\log_2\displaystyle \frac{x}{2}\right)\left(\log_2\displaystyle \frac{x}{8}\right) \\
&=&\left(\log_2x-1\right)\left(\log_2x-3\right)\\
&=&(t-1)(t-3)\\
&=&t^2-4t+3\\
&=&(t-2)^2-1) \end{eqnarray}}\)
\(\small{ \ t=2 \ }\)すなわち\(\small{ \ x=4 \ }\)のとき最小値\(\small{ \ -1 \ }\)
\(\small{ \ t=-1 \ }\)すなわち\(\small{ \ x=\displaystyle \frac{1}{2} \ }\)のとき最大値\(\small{ \ 8 \ }\)
(3)\(\small{ \ x\geqq2, \ y\geqq2, \ xy=16 \ }\)で底を\(\small{ \ 2 \ }\)とする対数をとると
\(\small{ \ \log_2x=t \ }\)とすると\(\small{ \ \log_2y=4-t \ }\)
\(\small{ \ t\geqq 1\ }\)かつ\(\small{ \ 4-t\geqq1 \ }\)より\(\small{ \ 1\leqq t \leqq 3 \ }\)
\(\small{\begin{eqnarray} \ \left(\log_2x\right)\left(\log_{2}y\right)&=&t(4-t)\\
&=&-t^2+4t\\
&=&-(t-2)^2+4 \ \end{eqnarray}}\)
\(\small{ \ t=2 \ }\)すなわち\(\small{ \ (x, \ y)=(4, \ 4) \ }\)のとき最大値\(\small{ \ 4 \ }\)
\(\small{ \ t=1, \ 3 \ }\)すなわち\(\small{ \ (x, \ y)=(2, \ 8), \ (8, \ 2) \ }\)のとき最大値\(\small{ \ 3 \ }\)

Point 対数関数の最大値・最小値
①括弧の\(\small{ \ 2 \ }\)乗は括弧内を置換して二次関数にする
②真数の最大最小は底の大きさに注意する
\(\small{ \ x, \ y \ }\)が等式\(\small{ \ \left(\log_2x\right)^2+\left(\log_2y\right)^2=\log_2x^3+\log_2y^3 \ }\)を満たすとき、\(\small{ \ \displaystyle \frac{x}{y} \ }\)の最大値と最小値を求めよ。
真数条件から\(\small{ \ x\gt0, \ y\gt0 \ }\)
\(\small{ \ X=\log_2x, \ Y=\log_2y \ }\)とおくと
\(\small{ \ X^2+Y^2=3X+3Y\cdots① \ }\)
また\(\small{ \ k=\log_2\displaystyle \frac{x}{y}=X-Y\cdots② \ }\)とおく
\(\small{ \ ① \ }\)から\(\small{ \ C:\left(X-\displaystyle \frac{3}{2}\right)^2+\left(Y-\displaystyle \frac{3}{2}\right)^2=\displaystyle \frac{9}{2} \ }\)
\(\small{ \ ② \ }\)から\(\small{ \ l:X-Y-k=0 \ }\)
よって直線\(\small{ \ l \ }\)と円\(\small{ \ C \ }\)が共有点を持つ範囲が\(\small{ \ k \ }\)の範囲である
円の中心\(\small{ \ \left(\displaystyle \frac{3}{2}, \ \displaystyle \frac{3}{2}\right) \ }\)と直線の距離を\(\small{ \ d \ }\)とすると
\(\small{ \ d\leqq \displaystyle \frac{3}{\sqrt{2}} \ }\)であればよい
\(\small{ \ d=\displaystyle \frac{\left|\displaystyle \frac{3}{2}-\displaystyle \frac{3}{2}-k\right|}{\sqrt{1+1}}\leqq\displaystyle \frac{3}{\sqrt{2}} \ }\)
\(\small{ \ \therefore |k|\leqq3 \ }\)
\(\small{ \ ①, \ ② \ }\)より
\(\small{ \ k=3 \ }\)すなわち\(\small{ \ (x, \ y)=(8, \ 1) \ }\)のとき最大値\(\small{ \ 8 \ }\)
\(\small{ \ k=-3 \ }\)すなわち\(\small{ \ (x, \ y)=(1, \ 8) \ }\)のとき最大値\(\small{ \ \displaystyle \frac{1}{8} \ }\)

