こんにちは、リンス(@Lins016)です。
今回は対数の性質について学習していこう。
対数とは
\(\small{ \ a^x \ }\)を指数っていうのと同じで、\(\small{ \ \log_ab \ }\)のように表される数のことを対数って言うんだ。
この\(\small{ \ \log_ab \ }\)の\(\small{ \ a, \ b \ }\)はともに正の数で、\(\small{ \ \log_ab=N \ }\)のとき\(\small{ \ a^N=b \ }\)が成り立つんだ。
対数と指数の関係
\(\small{ \ \log_ab=N \Leftrightarrow a^N=b \ }\)
対数の性質と計算方法
\(\small{ \ \log_aM+\log_aN=\log_aMN \ }\)
\(\small{ \ \log_aM-\log_aN=\log_a\displaystyle\frac{M}{N} \ }\)
\(\small{ \ \log_aM^r=r\log_aM \ }\)
\(\small{ \ \log_aa=1 \ }\)
\(\small{ \ \log_a1=0 \ }\)
対数の基本
\(\small{ \ 2^x=4 \ }\)は\(\small{ \ 2^x=2^2 \ }\)にして\(\small{ \ x=2 \ }\)って解けるけど、対数を知らないと\(\small{ \ 2^x=3 \ }\)って解けない。
指数関数のグラフを見ればわかるけど、\(\small{ \ 2^x=3 \ }\)を満たす\(\small{ \ x \ }\)って\(\small{ \ 1 \ }\)つだけ存在するよね。でもこの\(\small{ \ 2^x=3 \ }\)を満たす数っていうのは対数を利用しないと表すことは出来ないんだ。

対数は\(\small{ \ a^x=b \ }\)を満たす\(\small{ \ x \ }\)を表すことができる数で、この数\(\small{ \ x \ }\)が\(\small{ \ x=\log_ab \ }\)になるんだ。
\(\small{ \ \log_ab \ }\)の\(\small{ \ a \ }\)を底、\(\small{ \ b \ }\)を真数って言ってどちらも正の数になる。特に真数が正の数であることを真数条件って言うから覚えておこう。

対数の値
次に対数の値について考えてみよう。
\(\small{ \ \log_22=a \ }\)とすると\(\small{ \ 2^a=2 \ }\)だから\(\small{ \ a=1 \ }\)になる。
\(\small{ \ \log_24=b \ }\)とすると\(\small{ \ 2^b=4 \ }\)だから\(\small{ \ b=2 \ }\)、\(\small{ \ \log_28=c \ }\)とすると\(\small{ \ 2^c=8 \ }\)だから\(\small{ \ c=3 \ }\)になる。
つまり\(\small{ \ \log_aa^r=r \ }\)が成り立つんだ。
それじゃ\(\small{ \ \log_23 \ }\)の値について考えてみよう。
\(\small{ \ y=2^x \ }\)のグラフから考えて\(\small{ \ 1\lt \log_23 \lt 2 \ }\)の間って言えるよね。
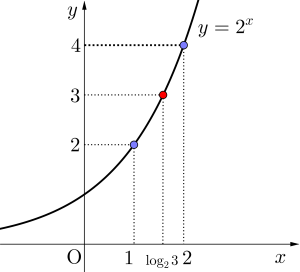
つまり対数っていうのは数字なんだ。当然数字だから加減乗除の四則計算を使うこともできる。
\(\small{ \ \sqrt{2} \ }\)や\(\small{ \ \sqrt[3]{2} \ }\)と同じように数を表す記号ってことを理解しておこう。
大きさも調べることができるからね。
例えば\(\small{ \ \log_35 \ }\)なら\(\small{ \ 1(=\log_33) \ }\)と\(\small{ \ 2(=\log_33^2) \ }\)の間の数だよね。
対数と有理数・無理数
次に\(\small{ \ 2^x=3 \ }\)の解になる\(\small{ \ \log_23 \ }\)は無理数か、それとも有理数かについて考えてみよう。
\(\small{ \ \log_23 \ }\)が有理数だとすると、
\(\small{ \ \log_23=\displaystyle\frac{p}{q} \ }\)(\(\small{ \ p, \ q \ }\)は自然数で互いに素)っておける。
この式を変形して\(\small{ \ 2^{\frac{p}{q}}=3 \ }\)
両辺を\(\small{ \ q \ }\)乗すると\(\small{ \ 2^p=3^q \ }\)
ここで左辺は偶数、右辺は奇数になる。
つまり矛盾が生じるから\(\small{ \ \log_23 \ }\)は無理数ってことになるんだ。
つまりこの形から整数にならない対数は無理数になるってことが言えそうだよね。そのことを考えて次の問題を見てみよう。
\(\small{ \ n \ }\)が正の整数のとき、\(\small{ \ \log_2n \ }\)が整数でない有理数になることはあるかどうか調べよ。
\(\small{ \ \log_2n \ }\)が有理数になるとすると、互いに素な自然数\(\small{ \ p, \ q \ }\)を用いて\(\small{ \ \log_2n=\displaystyle\frac{p}{q} \ }\)と表せるので、\(\small{ \ 2^p=n^q \ }\)が成り立つ。
このとき、両辺を比較すると\(\small{ \ n \ }\)は\(\small{ \ 2 \ }\)のみを素因数にもつ整数となるので、任意の整数\(\small{ \ m \ }\)を用いて\(\small{ \ n=2^m \ }\)となる。
このとき\(\small{ \ \log_2n=m \ }\)となり整数値になる。よって、\(\small{ \ \log_2n \ }\)が有理数ならその値は整数である。

対数の性質
次に対数の計算方法について学習しよう。
\(\small{ \ a^p=M, \ a^q=N \ }\)とすると、指数の計算から\(\small{ \ MN=a^{p+q} \ }\)、\(\small{ \ \displaystyle\frac{M}{N}=a^{p-q} \ }\) が言えるよね。
この\(\small{ \ 4 \ }\)つの式
\(\small{ \begin{eqnarray}
\left\{
\begin{array}{l}
a^p=M\\
a^q=N \\
a^{p+q}=MN\\
a^{p-q}=\displaystyle\frac{M}{N}
\end{array}
\right.
\end{eqnarray} \ }\)
の対数を考えると
\(\small{ \begin{eqnarray}
\left\{
\begin{array}{l}
p=\log_aM\\
q=\log_aN\\
p+q=\log_aMN\\
p-q=\log_a\displaystyle\frac{M}{N}
\end{array}
\right.
\end{eqnarray} \ }\)
が言えるよね。
この式から
\(\small{ \ \log_aM+\log_aN=\log_aMN \ }\)
\(\small{ \ \log_aM-\log_aN=\log_a\displaystyle\frac{M}{N} \ }\)
が言えるんだ。
この式って対数の計算の中でも非常に重要な式だから確実におさえておこう。
特に\(\small{ \ M=N \ }\)のとき
\(\small{ \ \log_aM+\log_aM=\log_aM^2 \ }\)になるから
\(\small{ \ 2\log_aM=\log_aM^2 \ }\)になる。
この式を一般化すると
\(\small{ \ \log_aM^r=r\log_aM \ }\)になるから、これも覚えておこう。
ってここまでは教科書に普通に書いてある対数の性質だけど、これをいつ使うかってことを考えてみよう。
例えば\(\small{ \ \log_254 \ }\)の真数は\(\small{ \ 54 \ }\)でこれを素因数分解すると\(\small{ \ 54=2\cdot3^3 \ }\)になるから
\(\small{\begin{eqnarray} \ \log_254&=&\log_22\cdot3^3\\
&=&\log_22+\log_23^3\\
&=&1+3\log_23 \ \end{eqnarray}}\)
って変形することができる。
真数が大きい数の場合、真数を素因数分解して対数の和の形に変形しよう。
対数の便利さ
対数って色々なところで使われているんだ。
みんなは数学Ⅱ以外では化学の水素イオン指数\(\small{ \ \mathrm{pH} \ }\)で見たと思うけど、地震の測定や、エネルギーの測定とかいろいろなところで対数は使われているんだ。
例えば\(\small{ \ 100000 \ }\)って数字に底\(\small{ \ 10 \ }\)の対数をとると\(\small{ \ \log_{10}100000=\log_{10}10^5=5 \ }\)ってなるよね。
対数をとることで大きい数を小さい数に変換して計算することが出来るから計算も楽になるし、大きい数と小さい数の比較も元の数より対数をとった数の方が比較しやすい場合もある。
昔の人が膨大な大きさの数の計算を少しでも簡単にしようと編み出したのが対数なんだ。
これ以外にも大きい数を小さい数に変換するのとは逆で、\(\small{ \ 0.0001 \ }\)に底\(\small{ \ 0.1 \ }\)の対数をとると\(\small{ \ \log_{0.1}0.0001=\log_{0.1}(0.1)^4=4 \ }\)っていうように対数をとることで非常に小さい値を大きくすることも出来る。
だから、ほとんど差がないような小さい数字を比較する場合、対数をとることで差がはっきりして比較しやすくなる。
高校数学では対数の便利さをきちんと教えてくれないけど、計算する数字によって、対数はとても便利な数になるんだ。
底の変換
対数を利用する上で重要なことがある。それは『底が同じである』ことなんだ。
対数の性質の計算で
\(\small{ \ \log_aM+\log_aN=\log_aMN \ }\)
\(\small{ \ \log_aM-\log_aN=\log_a\displaystyle\frac{M}{N} \ }\)
対数の和や差を真数の積や商にまとめるけど、これって底が同じ数じゃないといけないんだ。
例えば\(\small{ \ 1\mathrm{kg} \ }\)と\(\small{ \ 1\mathrm{g} \ }\)の和って\(\small{ \ 1001\mathrm{g} \ }\)か\(\small{ \ 1.001\mathrm{kg} \ }\)のようにどちらかの単位に揃えて計算するよね。
これと同じように対数の計算も必ず底が同じものじゃないと計算出来ないんだ。だから底が異なる対数が出てきたら底を同じに揃えないといけない。そのときに使うのが底の変換なんだ。
\(\small{ \ a^N=b \ }\)は\(\small{ \ N=\log_ab \ }\)だったけど
\(\small{ \ a^N=b \ }\) に底\(\small{ \ c \ }\)の対数をとると
\(\small{ \ \log_ca^N=\log_cb \ }\)
\(\small{ \ N\log_ca=\log_cb \ }\)より\(\small{ \ N=\displaystyle\frac{\log_cb}{\log_ca} \ }\)
つまり\(\small{ \ \log_ab=\displaystyle\frac{\log_cb}{\log_ca} \ }\)が言えるんだ。
これが底の変換なんだ。
底の変換を使うときは底をどんな数にしてもいいんだけど、できたら小さい数で素数のほうがいいから\(\small{ \ 2 \ }\)や\(\small{ \ 3 \ }\)あたりがいいかな。
例えば\(\small{ \ \log_49=\displaystyle\frac{\log_29}{\log_24}=\displaystyle\frac{2\log_23}{2}=\log_23 \ }\)のように変形できるからね。
\(\small{ \ \log_{10}2=a, \ \log_{10}3=b \ }\)とおくとき、次の値を\(\small{ \ a, \ b \ }\)で表せ。
(1)\(\small{ \ \log_{10}12 \ }\)
(2)\(\small{ \ \log_{10}5 \ }\)
(3)\(\small{ \ \log_{18}\displaystyle\frac{8}{9} \ }\)
(4)\(\small{ \ \log_{45}\sqrt[3]{24} \ }\)
(1)
\(\small{\begin{eqnarray} \ \log_{10}12&=&\log_{10}2^2\cdot3\\
&=&2\log_{10}2+\log_{10}3\\
&=&2a+b \ \end{eqnarray}}\)
(2)
\(\small{\begin{eqnarray} \ \log_{10}5&=&\log_{10}\displaystyle\frac{10}{2}\\
&=&\log_{10}10-\log_{10}2\\
&=&1-a \ \end{eqnarray}}\)
(3)
\(\small{\begin{eqnarray} \ \log_{18}\displaystyle\frac{8}{9}&=&\displaystyle\frac{\log_{10}8-\log_{10}9}{\log_{10}18}\\
&=&\displaystyle\frac{\log_{10}2^3-\log_{10}3^2}{\log_{10}2\cdot3^2}\\
&=&\displaystyle\frac{3\log_{10}2-2\log_{10}3}{\log_{10}2+2\log_{10}3}\\
&=&\displaystyle\frac{3a-2b}{a+2b} \ \end{eqnarray}}\)
(4)
\(\small{\begin{eqnarray} \ \log_{45}\sqrt[3]{24}&=&\displaystyle\frac{1}{3}\log_{45}24\\
&=&\displaystyle\frac{\log_{10}24}{3\log_{10}45}\\
&=&\displaystyle\frac{\log_{10}2^3\cdot3}{3\log_{10}3^2\cdot5}\\
&=&\displaystyle\frac{3\log_{10}2+\log_{10}3}{3\left(2\log_{10}3+\log_{10}5\right)}\\
&=&\displaystyle\frac{3a+b}{3(-a+2b+1)} \ \end{eqnarray}}\)

\(\small{ \ \log_{10}2=0.3010, \ \log_{10}3=0.4771 \ }\)が問題文に与えられているとき、\(\small{ \ \log_{10}5=1-\log_{10}2 \ }\)から\(\small{ \ \log_{10}5=0.6990 \ }\)が導けることを覚えておこう。
Point 対数とその性質
①対数と指数の関係式を理解する
②対数の性質の式を覚える
③底の変換公式を覚える
\(\small{ \ \theta \ }\)は\(\small{ \ 0\lt \theta \lt \displaystyle\frac{\pi}{2} \ }\)を満たしているとする。対数\(\small{ \ \log_{ \ \sin\theta}\cos\theta \ }\)の値が\(\small{ \ 2 \ }\)以下の整数であるとき、\(\small{ \ \sin\theta \ }\)のとりうる値をすべて求めよ。
\(\small{ \ 0\lt \theta \lt \displaystyle\frac{\pi}{2} \ }\)のとき
\(\small{ \ 0\lt \sin\theta \lt 1, \ 0\lt \cos\theta \lt 1 \ }\)より
\(\small{ \ \log_{ \ \sin\theta}\cos\theta\lt 0 \ }\)
条件より\(\small{ \ \log_{ \ \sin\theta}\cos\theta=1, \ 2 \ }\)
(i)\(\small{ \ \log_{ \ \sin\theta}\cos\theta=1 \ }\)のとき
\(\small{ \ \cos\theta=\sin\theta \ }\)
\(\small{ \ \therefore \sin\theta=\displaystyle\frac{1}{\sqrt{2}} \ }\)(\(\small{ \ \because0\lt \theta \lt \displaystyle\frac{\pi}{2} \ }\))
(ii)\(\small{ \ \log_{ \ \sin\theta}\cos\theta=2 \ }\)のとき
\(\small{ \ \cos\theta=\sin^2\theta \ }\)
\(\small{ \ \cos^2\theta+\cos\theta-1=0 \ }\)
\(\small{\begin{eqnarray} \ \sin\theta&=&\sqrt{1-\cos^2\theta}\\[5pt]
&=&\sqrt{1-\left(\displaystyle\frac{-1+\sqrt{5}}{2}\right)^2}\\[5pt]
&=&\sqrt{\displaystyle\frac{\sqrt{5}-1}{2}} \ \end{eqnarray}}\)
(i)(ii)より
\(\small{ \ \sin\theta=\displaystyle\frac{1}{\sqrt{2}}, \ \sqrt{\displaystyle\frac{\sqrt{5}-1}{2}} \ }\)


