こんにちは、リンス(@Lins016)です。今回は常用対数とその値について学習していこう。
常用対数
常用対数とは底が\(\small{ \ 10 \ }\)の対数のこと。
僕らは普段\(\small{ \ 10 \ }\)進法を使うことが多いよね。だから漢字のまま「常に用いる対数」って名前なのかもしれない。
\(\small{ \ 10 \ }\)進法は\(\small{ \ 10^n \ }\)ごとに\(\small{ \ 1, \ 10, \ 100,\cdots \ }\)と桁が増えていく。
この数を常用対数の真数に入れてみると\(\small{ \ \log_{10}1=0, \ \log_{10}10=1, \ \log_{10}100=2,\cdots \ }\)って真数が\(\small{ \ 1 \ }\)桁が増えるごとに数が\(\small{ \ 1 \ }\)ずつ増えていく。
対数を使うことで巨大な計算がより簡単に出来るんだけど、\(\small{ \ 10 \ }\)進法を利用した計算は常用対数を使うことで計算が簡単になるだけじゃなく、桁数なんかも簡単に求めることが出来るんだ。
\(\small{ \ \log_{10}2=0.3010 \ }\)、\(\small{ \ \log_{10}3=0.4771 \ }\)とすると
\(\small{ \ \log_{10}1=0 \ }\)
\(\small{ \ \log_{10}2=0.3010 \ }\)
\(\small{ \ \log_{10}3=0.4771 \ }\)
\(\small{ \ \log_{10}4=0.6020 \ }\)
\(\small{ \ \log_{10}5=0.6990 \ }\)
\(\small{ \ \log_{10}6=0.7781 \ }\)
\(\small{ \ \log_{10}7=0.8451 \ }\)
\(\small{ \ \log_{10}8=0.9030 \ }\)
\(\small{ \ \log_{10}9=0.9542 \ }\)
\(\small{ \ \log_{10}10=1\ }\)
常用対数表
対数って\(\small{ \ \log_ab \ }\)って書くけど、これって数字だったよね。
例えば\(\small{ \ \log_23 \ }\)は「\(\small{ \ 2 \ }\)を\(\small{ \ \log_23 \ }\)乗すると\(\small{ \ 3 \ }\)になる」って数字だから\(\small{ \ 2^1=2, \ 2^2=4 \ }\)から\(\small{ \ 1\lt \log_23 \lt2 \ }\)ってことが言えるよね。
常用対数は底が\(\small{ \ 10 \ }\)の対数なんだけど、\(\small{ \ 10 \ }\)進法を利用した計算は常用対数を利用する方が、底を他の数にするよりもなにかと便利なんだ。
化学で教わるpHなんかも常用対数が使われてるよね。その他にも地震のマグニチュードの計算とかみんなが知らないだけで、実は日常の色々な計算に常用対数が使われていることも結構あるんだ。だから常用対数の値っていうのはあらかじめ調べられていて教科書にも終わりの巻末ページの方に常用対数表が掲載されてるよね。
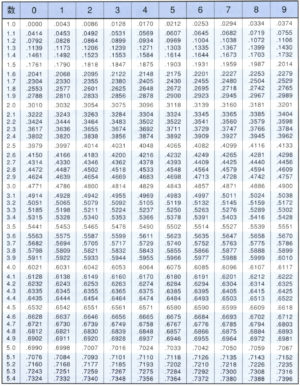
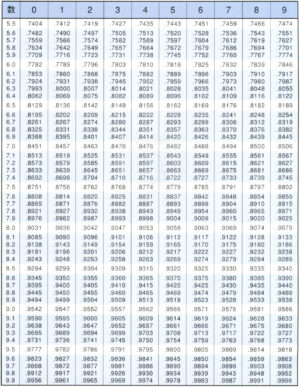
もちろん値を覚える必要はないけど、表の見方(使い方)ぐらいは覚えておこう。
例えば「\(\small{ \ \log_{10}314 \ }\)を求めよ」って言われたら常用対数表を使って
\(\small{\begin{eqnarray} \ \log_{10}314&=&\log_{10}3.14\times10^2\\
&=&\log_{10}3.14+\log_{10}10^2\\
&=&0.4969+2\\
&=&2.4969 \ \end{eqnarray}}\)
ってなるからね。
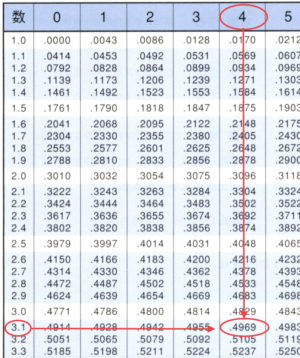

対数の底
対数って底が異なると対数の性質を利用した計算が出来ないから、底をそろえるってことが大切って話を以前したよね。
この底は、「問題文に記載されている対数の中で一番小さい素数にあわせる」っていうのが基本なんだけど、この常用対数を用いる問題の場合、底は一番小さい素数じゃなくて\(\small{ \ 10 \ }\)にそろえる必要があるんだ。
常用対数の問題は問題文に「\(\small{ \ \log_{10}2=0.3010, \ \log_{10}3=0.4771 \ }\)とする。」って常用対数の数値が与えられていることがほとんどだから、常用対数の数値が与えられているときは底は\(\small{ \ 10 \ }\)にそろえよう。
1桁の常用対数の値
常用対数の問題では「\(\small{ \ \log_{10}2=0.3010, \ \log_{10}3=0.4771 \ }\)とする。」っていうように\(\small{ \ \log_{10}2 \ }\)と\(\small{ \ \log_{10}3 \ }\)の値が与えられていることがほとんどなんだ。
この\(\small{ \ 2 \ }\)つの値が与えられていることで、\(\small{ \ 7 \ }\)以外の\(\small{ \ 1 \ }\)桁の常用対数の値を求めることが出来るんだ。
\(\small{ \ \log_{10}1=0 \ }\)
\(\small{ \ \log_{10}2=0.3010 \ }\)
\(\small{ \ \log_{10}3=0.4771 \ }\)
\(\small{ \ \begin{eqnarray}\log_{10}4&=&\log_{10}2^2\\
&=&2\log_{10}2\\
&=&2\times0.3010\\
&=&0.6020\end{eqnarray} \ }\)
\(\small{ \ \begin{eqnarray}\log_{10}5&=&\log_{10}\displaystyle\frac{10}{2}\\
&=&\log_{10}10-\log_{10}2\\
&=&1-0.3010\\
&=&0.6990\end{eqnarray} \ }\)
\(\small{ \ \begin{eqnarray}\log_{10}6&=&\log_{10}2\cdot3\\
&=&\log_{10}2+\log_{10}3\\
&=&0.3010+0.4771\\
&=&0.7781\end{eqnarray} \ }\)
\(\small{ \ \begin{eqnarray}\log_{10}8&=&\log_{10}2^3\\
&=&3\log_{10}2\\
&=&3\times0.3010\\
&=&0.9030\end{eqnarray} \ }\)
\(\small{ \ \begin{eqnarray}\log_{10}9&=&\log_{10}3^2\\
&=&2\log_{10}3\\
&=&2\times0.4771\\
&=&0.9542\end{eqnarray} \ }\)
ちなみに\(\small{ \ \log_{10}10=1\ }\)だからね。この\(\small{ \ 1 \ }\)桁の常用対数の値の求め方は桁数の問題の応用で利用するから確実におぼえておこう。
\(\small{ \ \log_{10}7 \ }\)の値
問題文によっては\(\small{ \ \log_{10}7=0.8451 \ }\)って与えられている問題もある。
\(\small{ \ \log_{10}2 \ }\)と\(\small{ \ \log_{10}3 \ }\)と\(\small{ \ \log_{10}7 \ }\)が与えられていたら\(\small{ \ 1 \ }\)桁の常用対数の値を求めることが出来ることになるよね。
でも\(\small{ \ \log_{10}2 \ }\)と\(\small{ \ \log_{10}3 \ }\)の値だけ与えられていても、\(\small{ \ \log_{10}7 \ }\)の値がどれくらいか調べる方法はあるんだ。
\(\small{ \ \log_{10}2=0.3010, \ \log_{10}3=0.4771 \ }\)のとき、
\(\small{ \ \begin{eqnarray}\log_{10}6&=&\log_{10}2\cdot3\\
&=&\log_{10}2+\log_{10}3\\
&=&0.3010+0.4771\\
&=&0.7781\end{eqnarray} \ }\)
\(\small{ \ \begin{eqnarray}\log_{10}8&=&\log_{10}2^3\\
&=&3\log_{10}2\\
&=&3\times0.3010\\
&=&0.9030\end{eqnarray} \ }\)
だから\(\small{ \ 0.7781\lt \log_{10}7 \lt 0.9030 \ }\)だよね。
でもこれだと結構値に幅があるよね。
もう少し幅を小さくしたいから、\(\small{ \ 48\lt49\lt50 \ }\)を利用して\(\small{ \ \log_{10}7 \ }\)を求めてみよう。
\(\small{ \ \begin{eqnarray}\log_{10}48&=&\log_{10}2^4\cdot3\\
&=&\log_{10}2^4+\log_{10}3\\
&=&4\log_{10}2+\log_{10}3\\
&=&4\times0.3010+0.4771\\
&=&1.6811\end{eqnarray} \ }\)
\(\small{ \ \begin{eqnarray}\log_{10}49&=&\log_{10}7^2\\
&=&2\log_{10}7\end{eqnarray} \ }\)
\(\small{ \ \begin{eqnarray}\log_{10}50&=&\log_{10}\displaystyle\frac{100}{2}\\
&=&\log_{10}10^2-\log_{10}2\\
&=&2\log_{10}10-\log_{10}2\\
&=&2\times1-0.3010\\
&=&1.699\end{eqnarray} \ }\)
\(\small{ \ \log_{10}48\lt \log_{10}49 \lt \log_{10}50 \ }\)より
\(\small{ \ 1.6811\lt 2\log_{10}7 \lt1.699 \ }\)
\(\small{ \ \therefore 0.84055\lt \log_{10}7 \lt0.8495 \ }\)
これで\(\small{ \ \log_{10}7 \ }\)の値の幅がだいぶ小さくなったよね。
\(\small{ \ \log_{10}2 \ }\)と\(\small{ \ \log_{10}3 \ }\)の値が与えられている場合、\(\small{ \ 2, \ 3, \ 5 \ }\)で素因数分解できる数字ではさむことで、他の素数の常用対数も調べることが出来るから、色々試してみよう。

Point 常用対数とその値
①\(\small{ \ \log_{10}2 \ }\)と\(\small{ \ \log_{10}3 \ }\)の値が与えられたとき他の常用対数の求め方を覚えておく

