こんにちは、リンス(@Lins016)です。
今回は指数関数を含む方程式の解き方について学習していこう。
指数関数を含む方程式の解き方
指数関数を含む方程式を解く場合、いきなり\(\small{ \ x=3 \ }\)みたいに答えが出るわけじゃない。
まずは\(\small{ \ 2^x=8 \ }\)っていうのが求まってから\(\small{ \ x=3 \ }\)って答えが求まるんだ。まずはこのことを頭に入れておこう。
①\(\small{ \ a^x=a^p \ }\)から\(\small{ \ x=p \ }\)
②\(\small{ \ 2^{2x}+2^{x+1}-3=0 \ }\)
\(\small{ \ 2^x=t \ }\)として
\(\small{ \ t^2+2t-3=0 \ }\)を解く
③\(\small{ \ 4^{x}+4^{-x}+2^x+2^{-x}=0 \ }\)
\(\small{ \ 2^x+2^{-x}=t \ }\)として
\(\small{ \ t^2+t-2=0 \ }\)を解く
指数を含む方程式の基本
最初に言ったけど指数関数を含む方程式はまず\(\small{ \ 2^x=8 \ }\)を求めて、そこから\(\small{ \ 2^x=2^3 \ }\)に変形して\(\small{ \ x=3 \ }\)って求めるのが基本なんだ。
だから\(\small{ \ a^x=p \ }\)の形にすることがまずは大切なんだ。この\(\small{ \ a^x=p \ }\)の形を常に解けるようにしよう。
次の方程式を解け。
(1)\(\small{ \ 2^x=4^{x-2} \ }\)
(2)\(\small{ \ 2^x=3 \ }\)
(3)\(\small{ \ 2^x=-3 \ }\)
(1)\(\small{ \ 2^x=4^{x-2} \ }\)
\(\small{ \ 2^x=2^{2(x-2)} \ }\)
\(\small{ \ x=2(x-2) \ }\)
\(\small{ \ \therefore x=4 \ }\)
(2)\(\small{ \ 2^x=3 \ }\)
\(\small{ \ \therefore x=\log_23 \ }\)
(3)\(\small{ \ 2^x=-3 \ }\)
\(\small{ \ 2^x\gt0 \ }\)より解なし

\(\small{ \ a^N=b \iff \log_ab=N \ }\)
つまり対数を知らないと\(\small{ \ 2^x=2^p \ }\)の形しか解けないけど、対数を教わることで\(\small{ \ 2^x=p \ (p\gt0) \ }\)の形も解くことが出来るんだ。
指数関数と二次方程式
次は指数を置換して二次方程式にする問題について考えていこう。
まずは以前書いた指数の置換について確認しておこう。
上の記事にもあるように基本的に置換するのは\(\small{ \ t=a^x \ }\)か\(\small{ \ t=a^x+a^{-x} \ }\)。
\(\small{ \ t=2^x \ }\)として\(\small{ \ t \ }\)の二次方程式になる場合、元の式には\(\small{ \ 4^x \ }\)や\(\small{ \ 2^{2x} \ }\)、\(\small{ \ \left(2^x\right)^2 \ }\)が入っているはずだからね。
\(\small{ \ t=2^x+2^{-x} \ }\)として\(\small{ \ t \ }\)の二次方程式になる場合は、元の式には\(\small{ \ 4^x+4^{-x} \ }\)や\(\small{ \ 2^{2x}+2^{-2x} \ }\)、\(\small{ \ \left(2^x\right)^2+\left(2^{-x}\right)^2 \ }\)が入っているはず。
最初に言ったようにいきなり\(\small{ \ x=3 \ }\)を求めるんじゃなくて\(\small{ \ 2^x=8 \ }\)を求めたいわけだから、どの文字を置けばいいか考えて問題を解こう。
次の方程式を解け。
(1)\(\small{ \ 4^x+2^{x+1}-3=0 \ }\)
(2)\(\small{ \ 9^x+9^{-x}-3^x-3^{-x}=0 \ }\)
(3)\(\small{ \begin{eqnarray}
\left\{
\begin{array}{l}
2^x+2^y=6 \\
2^{x+y} =8
\end{array}
\right.
\end{eqnarray} \ }\)
(1)\(\small{ \ 4^x+2^{x+1}-3=0 \ }\)
\(\small{ \ t=2^x \ }\)とおく(\(\small{ \ t\gt0 \ }\))
\(\small{ \ t^2+2t-3=0 \ }\)
\(\small{ \ (t+3)(t-1)=0 \ }\)
\(\small{ \ t\gt0 \ }\)より\(\small{ \ t=1 \ }\)
\(\small{ \ 2^x=1 \ }\)より\(\small{ \ x=0 \ }\)
(2)\(\small{ \ 9^x+9^{-x}-3^x-3^{-x}=0 \ }\)
\(\small{ \ t=3^x+3^{-x} \ }\)とおく(\(\small{ \ t\geqq2 \ }\))
\(\small{ \ t^2-t-2=0 \ }\)
\(\small{ \ (t-2)(t+1)=0 \ }\)
\(\small{ \ t\geqq2 \ }\)より\(\small{ \ t=2 \ }\)
\(\small{ \ 3^x+3^{-x}=2 \ }\)
\(\small{ \ a=3^x \ }\)とおく(\(\small{ \ a\gt0 \ }\))
\(\small{ \ a+\displaystyle\frac{1}{a}=2 \ }\)
\(\small{ \ a^2+1=2a \ }\)
\(\small{ \ (a-1)^2=0 \ }\)より\(\small{ \ a=1 \ }\)
\(\small{ \ 3^x=1 \ }\)より\(\small{ \ x=0 \ }\)
(3)\(\small{ \begin{eqnarray}
\left\{
\begin{array}{l}
2^x+2^y=6 \\
2^{x+y} =8
\end{array}
\right.
\end{eqnarray} \ }\)
\(\small{ \ X=2^x, \ Y=2^y \ }\)とおく(\(\small{ \ X\gt0, \ Y\gt0 \ }\))
\(\small{ \begin{eqnarray}
\left\{
\begin{array}{l}
X+Y=6 \\
XY =8
\end{array}
\right.
\end{eqnarray} \ }\)
\(\small{ \ Y=6-X \ }\)より\(\small{ \ X(6-x)=8 \ }\)
\(\small{ \ X^2-6X+8=0 \ }\)
\(\small{ \ (X-2)(X-4)=0 \ }\)
\(\small{ \ X=2, \ 4 \ }\)
\(\small{ \ (X, \ Y)=(2, \ 4), \ (4, \ 2) \ }\)
\(\small{ \ (2^x, \ 2^y)=(2, \ 4), \ (4, \ 2) \ }\)
\(\small{ \ \therefore(x, \ y)=(1, \ 2), \ (2, \ 1) \ }\)

指数を含む連立方程式も何を置けばいいのか考えて問題を解こう。あと置換したら範囲を必ず考えるようにね。
Point 指数関数を含む方程式の解き方
①置換して二次方程式へ変換する
②置換した文字の範囲を考える
\(\small{ \ 4^x+4^{-x}+a\left(2^x+2^{-x}\right)+6-a=0 \ }\)
この方程式が解を\(\small{ \ 4 \ }\)つもつための\(\small{ \ a \ }\)の値の範囲を求めよ。
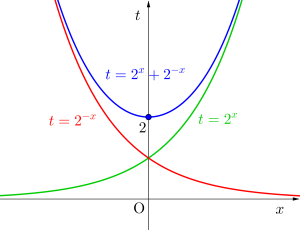
\(\small{ \ t=2^x+2^{-x} \ }\)とおくと(\(\small{ \ t\geqq2 \ }\))
\(\small{ \ t^2+at+4-a=0 \ }\)
ここで
\(\small{ \ t\lt2 \ }\)を満たす\(\small{ \ x \ }\)は存在しない
\(\small{ \ t=2 \ }\)のとき\(\small{ \ x=0 \ }\)
\(\small{ \ t\gt2 \ }\)を満たす\(\small{ \ x \ }\)は\(\small{ \ 2 \ }\)個存在する
よって\(\small{ \ 4^x+4^{-x}+a\left(2^x+2^{-x}\right)+6-a=0 \ }\)が\(\small{ \ 4 \ }\)つの解を持つためには\(\small{ \ t^2+at+4-a=0 \ }\)が\(\small{ \ t\gt2 \ }\)に\(\small{ \ 2 \ }\)つの解をもてばよい
\(\small{ \ t^2+at+4-a=0 \ }\)の判別式を\(\small{ \ D \ }\)、\(\small{ \ f(t)=t^2+at+4-a \ }\)とすると
\(\small{ \begin{eqnarray}
\left\{
\begin{array}{l}
D=a^2-4(4-a)\gt0\\
-\displaystyle\frac{a}{2}\gt2\\
f(2)=a+8\gt0
\end{array}
\right.
\end{eqnarray} \ }\)を満たせばよい
\(\small{ \begin{eqnarray}
\left\{
\begin{array}{l}
a\lt-2-2\sqrt{5}, \ a\gt-2+2\sqrt{5}\\
a\lt-4\\
a\gt-8
\end{array}
\right.
\end{eqnarray} \ }\)
よって求める\(\small{ \ a \ }\)の値の範囲は
\(\small{ \ -8\lt a\lt-2-2\sqrt{5} \ }\)

あとは解の配置の問題になるから、二次方程式の解の配置の解き方は確実におさえておこう。

