こんにちは、リンス(@Lins016)です。
今回は指数関数の最大・最小について学習していこう。
指数関数の最大値・最小値に関する問題
指数関数\(\small{ \ y=a^x \ }\)といえば、\(\small{ \ a \gt 1 \ }\)の場合単調増加、\(\small{ \ 0 \lt a \lt 1 \ }\)の場合単調減少になる関数だから、そんなに難しく考えなくても良さそうだよね。
でも実際は、\(\small{ \ a^x \ }\)や\(\small{ \ a^x+a^{-x} \ }\)を\(\small{ \ t \ }\)と置換して、二次関数や三次関数になる問題がほとんどだから、そのパターンについてしっかりと学習しておこう。
まずは指数関数の置換について復習しておこう。
① \(\small{ \ y=a^x \ }\)で表された関数
② \(\small{ \ t=a^x \ }\)と置換した関数
③\(\small{ \ t=a^x+a^{-x} \ }\)と置換した関数
④相加平均\(\small{ \ \geqq \ }\)相乗平均の利用
\(\small{ \ y=a^x \ }\)で示された関数
\(\small{ \ y=a^x \ }\)は\(\small{ \ a \gt 1 \ }\)なら単調増加、\(\small{ \ 0\lt a \lt 1 \ }\)なら単調減少になるんだったよね。
だから\(\small{ \ y=a^x \ }\)は\(\small{ \ a \gt 1 \ }\)か\(\small{ \ 0 \lt a \lt 1 \ }\)で分けて考えよう。
\(\small{ \ x \ }\)に定義域が存在しないとき最大値・最小値ともに存在しない。だってグラフはずっと増加または減少し続けるからね。
逆に閉区間(両端を含む区間)の定義域が存在すれば、最大値・最小値ともに存在する。
高校数学では\(\small{ \ a^x \ }\)の\(\small{ \ a \ }\)が正の数だけ学習するから\(\small{ \ a^x \ }\)は常に正の値になる。定義域が存在しないと最小値はなしってことになるけど、\(\small{ \ y=a^x \ }\)は\(\small{ \ 0 \ }\)より大きいってことは言えるよね。
このことが『\(\small{ \ t=a^x \ }\)と置換した関数』に利用されるからしっかりと覚えておこう。
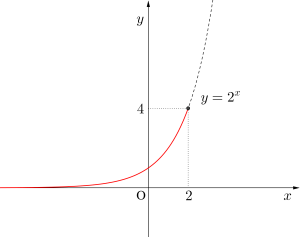
(1)\(\small{ \ y=2^x \ (x\leqq2 ) \ }\)の最大値と最小値を求めよ。
(2)\(\small{ \ y=\left(\displaystyle \frac{1}{2}\right)^x \ (1\leqq x \leqq 3) \ }\)の最大値と最小値を求めよ。
(3)\(\small{ \ y=a^x \ (-1\leqq x \leqq 3) \ }\)
(1)
\(\small{ \ y=2^x \ }\)は単調増加のグラフより
\(\small{x=2 \ }\)のとき最大値\(\small{\quad4}\)
最小値 なし
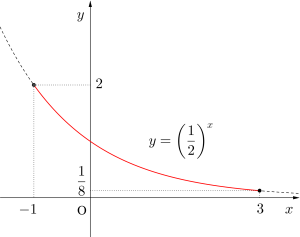
(2)
\(\small{y=\left(\displaystyle \frac{1}{2}\right)^x}\)は単調減少のグラフより
\(\small{x=-1\hspace{ 3pt }}\)のとき最大値\(\small{\quad2}\)
\(\small{x=3\quad}\)のとき最小値\(\small{\quad\displaystyle \frac{1}{8}}\)
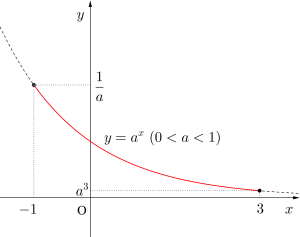
(3)
①\(\small{ \ y=a^x(0\lt a \lt 1)}\)のとき
\(\small{y=a^x}\)は単調減少のグラフより
\(\small{x=-1\hspace{ 3pt }}\)のとき最大値\(\small{\quad\displaystyle \frac{1}{a}}\)
\(\small{x=3\quad}\)のとき最小値\(\small{\quad a^3}\)
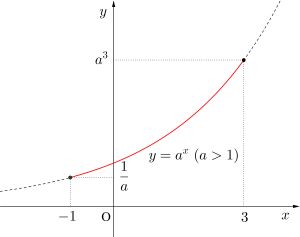
②\(\small{ \ y=a^x(a \gt 1)}\)のとき
\(\small{y=a^x}\)は単調増加のグラフより
\(\small{x=3\quad}\)のとき最大値\(\small{\quad a^3}\)
\(\small{x=-1\hspace{ 3pt }}\)のとき最小値\(\small{\quad \displaystyle \frac{1}{a}}\)

\(\small{ \ t=a^x \ }\)と置換した関数
\(\small{ \ t=a^x \ }\)って置換することとによって与えられた関数が二次関数や三次関数になる問題は、問題文から自分で判断しないといけない。
注目するところは何を\(\small{ \ t \ }\)って置換するかってことになるよね。\(\small{ \ t \ }\)は\(\small{ \ t^2 \ }\)や\(\small{ \ t^3 \ }\)になりそうな文字から判断して\(\small{ \ t \ }\)を定めよう。
その時に重要になるのが\(\small{ \ t=a^x \ }\)と置換したら\(\small{ \ (a^2)^x=a^{2x}=(a^x)^2 \ }\)は全て\(\small{ \ t^2 \ }\)になるってこと。
つまり問題文に\(\small{ \ 4^x \ }\)や\(\small{ \ 2^{2x} \ }\)や\(\small{ \ (2^x)^2 \ }\)と\(\small{ \ 2^x \ }\)があれば\(\small{ \ t=2^x \ }\)とおくことで\(\small{ \ t \ }\)の二次関数に変形できるってことだよね。
ちなみに\(\small{ \ 2^x \ }\)の部分については\(\small{ \ 2^{x+3} \ }\)とかでも構わない。だって\(\small{ \ 2^{x+3} \ }\)は\(\small{ \ 2^3\cdot2^x=8\cdot2^x=8t \ }\)って変形して置換することができるからね。
もちろん変形して三次関数になるなら\(\small{ \ 8^x \ }\)や\(\small{ \ 2^{3x} \ }\)が問題文にあることになるよね。
置換して二次関数や三次関数になる問題をきちんと見極められるようになるためには、指数関数の最大最小問題を見たときに、何を\(\small{ \ t \ }\)とおけばいいかをしっかりと考えよう。
(1)\(\small{ \ y=4^x -2^{x+3}+10 \ }\)の最大値と最小値を求めよ。
(2)\(\small{ \ y=a^{2x}-6a^x+10 \ (1 \leqq x \leqq 2) \ }\)の最大値と最小値を求めよ。ただし\(\small{ \ a\gt1 \ }\)とする。
(1)
\(\small{\begin{eqnarray}
y&=&4^x-2^{x+3}+10\\
&=&(2^x)^2-2^3\cdot2^x+4\\
&=&(2^x)^2-8\cdot2^x+4
\end{eqnarray}}\)
\(\small{ \ 2^x=t \ }\)とおくと\(\small{ \ (t\gt0)}\)
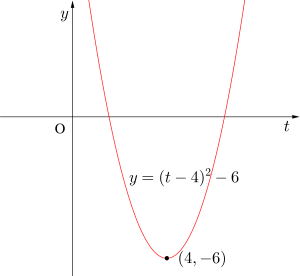
\(\small{\begin{eqnarray}y&=&t^2-8t+10\\
&=&(t-4)^2-6
\end{eqnarray}}\)
\(\small{t=4 \Leftrightarrow 2^x=4}\)
\(\small{\therefore \ x=2 \ }\)のとき最小値\(\small{ \ -6 \ }\)
最大値なし
(2)
\(\small{y=a^{2x}-6a^x+10}\)
\(\small{ \ a^x=t \ }\)とおくと\(\small{ \ t\gt0}\)
\(\small{\begin{eqnarray}y&=&t^2-6t+10\\
&=&(t-3)^2+1\end{eqnarray}}\)
ここで\(\small{ \ a\gt1 \ }\)より\(\small{ \ a\leqq t\leqq a^2}\)
①\(\small{ \ a^2\lt 3}\)
\(\small{\quad \therefore 1\lt a \lt \sqrt{3} \ }\)のとき
\(\small{ \ t=a \ }\)のとき\(\small{ \ \therefore x=1 \ }\)のとき
最大値\(\small{ \ a^2-6a+10}\)
\(\small{t=a^2 \ }\)のとき\(\small{\therefore x=2 \ }\)のとき
最小値\(\small{ \ a^4-6a^2+10}\)

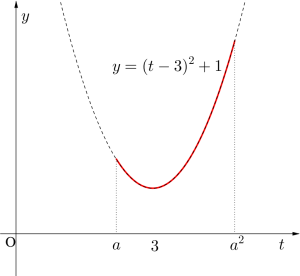
②\(\small{ \ \displaystyle \frac{a+a^2}{2}\lt 3 \leqq a^2}\)
\(\small{\quad \therefore \sqrt{3}\leqq a \lt 2 \ }\)のとき
\(\small{t=a \ }\)のとき\(\small{\therefore x=1 \ }\)のとき
最大値\(\small{ \ a^2-6a+10}\)
\(\small{t=3 \ }\)のとき \(\small{\therefore x=\log_a3 \ }\)のとき
最小値\(\small{ \ 1}\)

③\(\small{ \ a \lt 3 \leqq \displaystyle \frac{a+a^2}{2} }\)
\(\small{\quad \therefore 2\leqq a \lt 3 \ }\)のとき
\(\small{t=a^2 \ }\)のとき \(\small{\therefore x=2 \ }\)のとき
最大値\(\small{ \ a^4-6a^2+10}\)
\(\small{t=3 \ }\)のとき \(\small{\therefore x=\log_a3 \ }\)のとき
最小値\(\small{ \ 1}\)
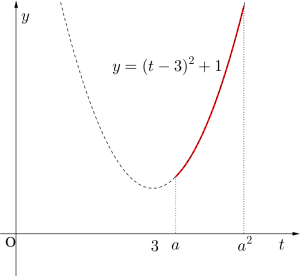
④\(\small{ \ a \gt 3 \ }\)のとき
\(\small{t=a^2 \ }\)のとき \(\small{\therefore x=2 \ }\)のとき
最大値\(\small{ \ a^4-6a^2+10}\)
\(\small{t=a \ }\)のとき \(\small{\therefore x=1 \ }\)のとき
最小値\(\small{ \ a^2-6a+10}\)

\(\small{t=a^x+a^{-x} \ }\)と置換した関数
\(\small{ \ t=a^x+a^{-x} \ }\)と置換することによって与えられた関数が二次関数になる問題は、\(\small{ \ t=a^x \ }\)と置換した関数と同じで問題文から自分で判断しないといけない。
注目するところは\(\small{ \ a^x \ }\)と\(\small{ \ a^{-x} \ }\)以外にも\(\small{ \ a^{2x} \ }\)と\(\small{ \ a^{-2x} \ }\)や\(\small{ \ a^{3x} \ }\)と\(\small{ \ a^{-3x} \ }\)が存在するということ。
中には\(\small{ \ a^{x}+a^{-x} \ }\)の部分が\(\small{ \ a^{3+x}+a^{3-x} \ }\)みたいに少しわかりにくい形で示してある問題もあるけど、問題文をよく読んで判断しよう。
このタイプの問題で注意しないといけないのが\(\small{ \ t \ }\)の範囲。\(\small{ \ x \ }\)に定義域が与えられてなくても、\(\small{ \ t=a^x+a^{-x} \ }\)と置換して、相加相乗を利用すると\(\small{ \ t \geqq 2 \ }\)になる。
「置換したら範囲が変更すること」に注意して問題を解こう。
(1)\(\small{ \ y=4^x+4^{-x} -2^{x+3}-2^{3-x}+16 \ }\)の最大値と最小値を求めよ。
(2)\(\small{ \ y=4^x+4^{-x} -a\cdot 2^x-a\cdot 2^{-x}+16 \ }\)の最小値を求めよ。
(1)
\(\small{\begin{eqnarray}
y&=&4^x+4^{-x}-2^{x+3}-2^{-x+3}+16\\
&=&(2^x)^2+(2^{-x})^2-8(2^x+2^{-x})+16\end{eqnarray} \ }\)
\(\small{ \ t=2^x+2^{-x} \ }\)とおくと
相加平均と相乗平均の関係より
\(\small{ \ t=2^x+2^{-x}\geqq 2\sqrt{2^x\cdot2^{-x}}=2 \ }\)より\(\small{ \ t\geqq2 \ }\)
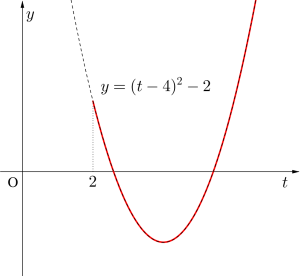
\(\small{\begin{eqnarray}
y&=&(t^2-2)-8t+16\\
&=&t^2-8t+14\\
&=&(t-4)^2-2\end{eqnarray}}\)
\(\small{\therefore t=4 \ }\)のとき最小値をとる
\(\small{ \ t=2^x+2^{-x}=4 \ }\)より
\(\small{ \ 2^x=a \ }\)とおくと\(\small{ \ a+\displaystyle \frac{1}{a}=4 \ }\)
\(\small{ \ a^2-4a+1=0 \ }\)
\(\small{ \ \therefore a=2\pm\sqrt{3} \ }\)
\(\small{ \ x=\log_2(2\pm\sqrt{3})}\)
\(\small{ \ x=\log_2(2\pm\sqrt{3}) \ }\)のとき最小値\(\small{ \ -2 \ }\)
(2)
\(\small{ \ y=4^x+4^{-x}-2a(2^x+2^{-x})+16}\)
\(\small{ \ 2^x+2^{-x}=t \ }\)とおくと
相加平均と相乗平均の関係より
\(\small{ \ t=2^x+2^{-x}\geqq 2\sqrt{2^x\cdot2^{-x}}=2 \ }\)より
\(\small{ \ t\geqq2 \ }\)
\(\small{\begin{eqnarray}
y&=&(t^2-2)-2at+16\\
&=&t^2-2at+14\\
&=&(t-a)^2-a^2+16\end{eqnarray}}\)
①\(\small{ \ a\geqq 2 \ }\)のとき
\(\small{ \ t=a \ }\)のとき最小
\(\small{ \ 2^x+2^{-x}=a \ }\)
\(\small{ \ 2^x=k \ }\)とおくと
\(\small{ \ k+\displaystyle \frac{1}{k}=a \ }\)
\(\small{ \ k^2-ak+1=0 \ }\)
\(\small{ \ k=\displaystyle \frac{a\pm \sqrt{a^2-4}}{2}}\)
\(\small{ \ \therefore x=\log_2\displaystyle \frac{a\pm \sqrt{a^2-4}}{2}}\)
よって\(\small{ \ x=\log_2\displaystyle \frac{a\pm \sqrt{a^2-4}}{2} \ }\)のとき
最小値\(\small{ \ 14 \ }\)
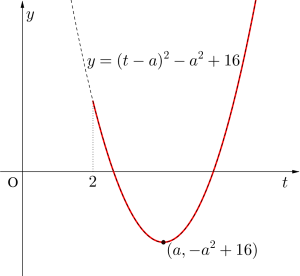
②\(\small{ \ a\lt 2 \ }\)のとき
\(\small{ \ t=2 \ }\)のとき最小
\(\small{ \ 2^x+2^{-x}=2}\)
\(\small{ \ 2^x=k \ }\)とおくと
\(\small{ \ k+\displaystyle \frac{1}{k}=2 \ }\)
\(\small{ \ k^2-2k+1=0 \ }\)
\(\small{ \ (k-1)^2=0}\)
\(\small{ \ k=1 \quad \therefore x=1}\)
よって\(\small{ \ x=1 \ }\)のとき最小値\(\small{ \ 18-4a}\)


相加平均相乗平均を利用した最大最小
ここまでで\(\small{ \ t=a^x \ }\)や\(\small{ \ t=a^x+a^{-x} \ }\)って置換すると与えられた関数が二次関数や三次関数になる問題は、解けるようになったと思う。
だけど\(\small{ \ a^x \ }\)を\(\small{ \ t \ }\)とおいてみたら\(\small{ \ pt+\displaystyle \frac{q}{t} \ }\)のように係数部分を無視すると逆数の和の形になる問題もあるんだ。
通分して分子を\(\small{ \ t \ }\)の二次関数にしても分母に\(\small{ \ t \ }\)があるから分子の最大・最小を調べても、そのとき分母も変わるから、分子が最大・最小になるとき、全体が最大・最小になるとは言えないよね。
理系の生徒は通分して分数関数を微分すれば問題ないけど、文系の生徒の場合は分数関数の微分なんて教わってないしね。
そこで考えるのが相加平均と相乗平均の関係式。この関係式は不等式になっているから、最小値や最大値のどちらか一方は求めることが出来そうだよね。
ただし相加相乗を利用する場合、当然だけど\(\small{ \ t\gt 0 \ }\)じゃないと利用できないから注意しておこう。って言ってもこの指数関数の場合は\(\small{ \ t=a^x \ }\)とすると\(\small{ \ t \gt 0 \ }\)だから利用できるよね。
また、\(\small{ \ pt+\displaystyle \frac{q}{t}=2\sqrt{pt\cdot\displaystyle \frac{q}{t}} \ }\)の等号成立は\(\small{ \ pt=\displaystyle \frac{q}{t} \ }\)の時になるから、\(\small{ \ t \ }\)とおいたまま\(\small{ \ t \ }\)を求めてから、\(\small{ \ x \ }\)を求めよう。
逆数の和をみたら相加相乗を思い出せるように日頃から準備しておこう。
\(\small{ \ y=2^{x+1}+18\cdot2^{-x}}\)の最大値と最小値を求めよ。
\(\small{\begin{eqnarray} \ y&=&2^{x+1}+18\cdot2^{-x}\\
&=&2\cdot2^x+18\cdot2^{-x} \ \end{eqnarray}}\)
相加平均・相乗平均の関係より
\(\small{ \ 2\cdot2^x+18\cdot2^{-x} \geqq 2\sqrt{2\cdot2^x \cdot\displaystyle \frac{18}{2^{-x}}}=12}\)
よって最小値は\(\small{ \ 12 \ }\)
そのとき\(\small{ \ 2\cdot2^x=18\cdot2^{-x}\\
2^x=9\cdot2^{-x}}\)
\(\small{ \ 2^x=t \ }\)とおくと\(\small{ \ t\gt0}\)
\(\small{ \ t^2=9 \quad t=3}\)
\(\small{ \ 2^x=3 \ \therefore x=\log_23}\)
Point 指数関数の最大・最小
①置換して二次関数か三次関数、相加相乗の利用
②置換した文字の範囲を考える

二次関数の最大最小は平方完成、三次関数の最大最小は微分だからね。

