こんにちは、リンス(@Lins016)です。今回は対数関数を含む方程式(対数方程式)とその解き方について学習していこう。
対数関数を含む方程式(対数方程式)の解き方
対数関数を含む方程式は大きく分けて\(\small{ \ 2 \ }\)つのタイプがある。
それは\(\small{ \ \log_2(x-2) \ }\)のような真数条件を考える問題と\(\small{ \ \log_2x \ }\)を\(\small{ \ t \ }\)と置換して二次方程式を解く問題だ。
この\(\small{ \ 2 \ }\)つのパターンの解き方や見分け方について考えていこう。
真数条件を考える対数方程式
\(\small{ \ \log_2(x-4)+\log_2(x+2)=4 \ }\)
対数を置換する対数方程式
\(\small{ \ \left(\log_2x\right)^2-\log_2x^2-3=0 \ }\)
対数関数を含む方程式(対数方程式)の解き方(基本)
対数関数を含む方程式を解くとき、いきなり\(\small{ \ x=4 \ }\)みたいに方程式の解が求められるわけじゃない。
まずは\(\small{ \ \log_2x=4 \ }\)や\(\small{ \ \log_2(x-4)=3 \ }\)、\(\small{ \ \log_2(2x-3)=\log_2(x+1) \ }\)のように\(\small{ \ x \ }\)を含む対数が求まってから\(\small{ \ x=4 \ }\)って解が求められるんだ。
\(\small{ \ \log_2x=4 \ }\)なら\(\small{ \ 2^x=2^4 \ }\)、\(\small{ \ \log_2(x-4)=3 \ }\)なら\(\small{ \ x-4=2^3 \ }\)、\(\small{ \ \log_2(2x-3)=\log_2(x+1) \ }\) なら\(\small{ \ 2x-3=x+1 \ }\) って対数をなくして真数の比較から解を求めるんだ。
つまり対数関数を含む方程式の解を求めるには『対数関数を含む項=整数』の形か、底が同じ『対数関数を含む項=対数関数を含む項』の形にしないといけない。
\(\small{ \ \log_2(x-4)+\log_2(x+1)=3 \ }\)のような対数関数の和や差の項がある状態だと、もう一工夫必要になるから式を整理して『\(\small{ \ \log_2(f(x)) \ }\)=定数(対数関数を含む項=整数)』または『\(\small{ \ \log_2f(x)=\log_2g(x) \ }\)(対数関数を含む項=対数関数を含む項)』の形にしよう。
対数関数を含む方程式(対数方程式)のパターン
対数関数を含む方程式には\(\small{ \ 2 \ }\)つのパターンがあるんだ。
問題を見て、どっちのパターンの問題なのか理解する必要があるから、まずはパターンを押さえよう。
\(\small{ \ 1 \ }\)つ目は真数条件を考えるパターン
①\(\small{ \ \log_2(x-4)+\log_2(x+2)=4 \ }\)
この問題の特徴は真数が\(\small{ \ x \ }\)の一次式や二次式になっていて、真数条件を考える問題になる。
\(\small{ \ 2 \ }\)つ目は対数を置換するパターン
②\(\small{ \ \left(\log_2x\right)^2-\log_2x^2-3=0 \ }\)
この問題は対数を\(\small{ \ 2 \ }\)乗した\(\small{ \ \left(\log_2x\right)^2 \ }\)のような(対数)\(\small{^2 \ }\)がある問題になる。
問題を見てどっちのパターンかって気付くようにしよう。
②は対数を括弧した\(\small{ \ 2 \ }\)乗があるから気付きやすいかな。
それじゃ次にそれぞれの解き方を見ていこう。
真数条件を考える対数関数を含む方程式(対数方程式)の解き方
真数条件(真数が正の値になること)を考えない対数はないんだけど、特に真数が\(\small{ \ x \ }\)じゃなくて\(\small{ \ \log_2(x-2) \ }\)のように\(\small{ \ x \ }\)の一次式、または\(\small{ \ \log_2(x^2-x-2) \ }\)のような\(\small{ \ x \ }\)の二次式になっている対数は真数条件をきちんと求めないといけないよね。
真数条件についてはこの記事で確認しておこう。
このパターンの問題は左辺と右辺を\(\small{ \ 1 \ }\)つの対数の形に変形して真数を比較して解くんだ。
\(\small{ \ 1 \ }\)つの対数の形ってどんな形かっていうのは次の問題を解き方で確認しよう。
\(\small{ \ \log_2(x-4)+\log_2(x+2)=4 \ }\)
この問題だと左辺は対数が\(\small{ \ \log_2(x-4) \ }\)と\(\small{ \ \log_2(x+2) \ }\)の\(\small{ \ 2 \ }\)つあるから対数の性質を使って\(\small{ \ 1 \ }\)つの対数にまとめよう。
(左辺)
\(\small{\begin{eqnarray}&=&\log_2(x-4)+\log_2(x+2)\\
&=&\log_2(x-4)(x+2) \ \end{eqnarray}}\)
これが\(\small{ \ 1 \ }\)つにまとめた対数の形ってことね。
次に右辺は整数だよね。左辺は対数で右辺は整数だと比較しにくいから、整数も対数にしよう。
整数を対数にする場合、普通に変換できる人はいいけど、変換が苦手な人は整数の後ろに変形したい底の対数\(\small{ \ \log_aa \ }\)をつける(掛ける)ようにしよう。
\(\small{ \ \log_aa=1 \ }\)だから整数にこれを掛けても値は変わらないよね。
この問題の場合、左辺の対数の底は\(\small{ \ 2 \ }\)だから右辺の整数は後ろに\(\small{ \ \log_22 \ }\)を掛けて
(右辺)
\(\small{\begin{eqnarray}&=&3\\
&=&4\log_22\\
&=&\log_22^4\\
&=&\log_216 \ \end{eqnarray}}\)
ってすれば整数を対数に簡単に変えられるからね。
ちなみにこの方法は対数不等式を解くとき特に有効だから覚えておこう。
そしたら
\(\small{ \ \log_2(x-4)+\log_2(x+2)=4 \ }\)は
\(\small{ \ \log_2(x-4)(x+2)=\log_216 \ }\)になるから
\(\small{ \ (x-4)(x+2)=16\cdots(\ast) \ }\)を解けばいいんだ。
でも\(\small{ \ \ast }\)の解が答えじゃないから注意しよう。真数条件を満たしてるものだけが解になるからね。
真数条件は\(\small{ \ x-4\gt0 \ }\)かつ\(\small{ \ x+2\gt0 \ }\)だから\(\small{ \ x\gt4 \ }\)。
\(\small{ \ \ast}\)を解くと\(\small{ \ x=6, \ -4 \ }\)だから答えは\(\small{ \ x=6 \ }\)になるんだ。
このパターンの問題のとき、絶対に真数条件を忘れないようにしよう。

対数の和を\(\small{ \ 1 \ }\)つの対数にまとめたりするのも底が同じじゃないと出来ないからね。
対数関数を置換する方程式の解き方
次に②の対数関数を置換する問題について考えてみよう。
この問題はさっきも話したけど『(対数)\(\small{^2 \ }\)がある場合』って覚えておこう。
対数の和なら\(\small{ \ \log_aM+\log_aN=\log_aMN \ }\)って変形できるけど、対数の積\(\small{ \ \left(\log_aM\right)\left(\log_aN\right) \ }\)はこれ以上変形することができないんだ。
当然\(\small{ \ \left(\log_2x\right)^2 \ }\)も変形することができない。だから\(\small{ \ \log_2x=t \ }\)って置換して問題を解いていこうってことになるんだ。
この置換するとき\(\small{ \ t=\log_2x \ }\)は真数条件から\(\small{ \ x\gt0 \ }\)だけど、\(\small{ \ t \ }\)はすべての実数をとる。だから\(\small{ \ t \ }\)と置換してできた\(\small{ \ t \ }\)の二次方程式の解はすべて解になるからね。
対数の底が\(\small{ \ 1 \ }\)より大きくても小さくてもどちらにしても\(\small{ \ t=\log_ax \ }\)は\(\small{ \ x\gt0 \ }\)で\(\small{ \ t \ }\)はすべての範囲をとるからね。
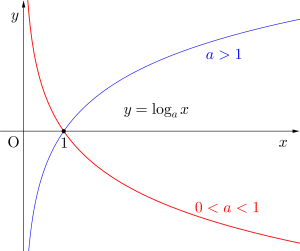
これはグラフを考えれば明らかだよね。
\(\small{ \ \left(\log_2x\right)^2-\log_2x^2-3=0 \ }\)を解いてみよう。
\(\small{ \ \left(\log_2x\right)^2-2\log_2x-3=0 \ }\)
\(\small{ \ t=\log_2x \ }\)とおくと
\(\small{ \ t^2-2t-3=0 \ }\)
\(\small{ \ (t-3)(t+1)=0 \ }\)
\(\small{ \ t=-1, \ 3 \ }\)
\(\small{ \ \log_2x=-1, \ 3 \ }\)
\(\small{ \ \therefore x=\displaystyle\frac{1}{2}, \ 8 \ }\)
\(\small{ \ t \ }\)はすべての実数をとるから正でも負でも\(\small{ \ x \ }\)は存在するよね。
(対数)\(\small{^2 \ }\)を見たら置換するって覚えておこう。
次の方程式を解け。
(1)\(\small{ \ \log_{10}(x-1)+\log_{10}(x+2)=1 \ }\)
(2)\(\small{ \ \log_{\frac{1}{9}}(x+7)=1+\log_{\frac{1}{3}}(6x-3) \ }\)
(3)\(\small{ \ \left(\log_2x\right)^2-\log_2x^3-4=0 \ }\)
(1)\(\small{ \ \log_{10}(x-1)+\log_{10}(x+2)=1 \ }\)
\(\small{ \ \log_{10}(x-1)(x+2)=\log_{10}10 \ }\)
\(\small{ \ (x-1)(x+2)=10 \ }\)
\(\small{ \ x^2+x-12=0 \ }\)
\(\small{ \ (x-3)(x+4)=0 \ }\)
真数条件は\(\small{ \ x\gt1 \ }\)より\(\small{ \ x=3 \ }\)
(2)\(\small{ \ \log_{\frac{1}{9}}(x+7)=1+\log_{\frac{1}{3}}(6x-3) \ }\)
\(\small{ \ \displaystyle\frac{\log_{\frac{1}{3}}(x+7)}{\log_{\frac{1}{3}}\frac{1}{9}}=\log_{\frac{1}{3}}\displaystyle\frac{1}{3}+\log_{\frac{1}{3}}(6x-3) \ }\)
\(\small{ \ \displaystyle\frac{\log_{\frac{1}{3}}(x+7)}{2}=\log_{\frac{1}{3}}\displaystyle\frac{1}{3}(6x-3) \ }\)
\(\small{ \ \log_{\frac{1}{3}}(x+7)=2\log_{\frac{1}{3}}(2x-1) \ }\)
\(\small{ \ \log_{\frac{1}{3}}(x+7)=\log_{\frac{1}{3}}(2x-1)^2 \ }\)
\(\small{ \ x+7=(2x-1)^2 \ }\)
\(\small{ \ 4x^2-5x-6=0 \ }\)
\(\small{ \ (4x+3)(x-2)=0 \ }\)
真数条件は\(\small{ \ x\gt\displaystyle\frac{1}{2} \ }\)より\(\small{ \ x=2 \ }\)
(3)\(\small{ \ \left(\log_2x\right)^2-\log_2x^3-4=0 \ }\)
\(\small{ \ \left(\log_2x\right)^2-3\log_2x-4=0 \ }\)
\(\small{ \ \log_2x=t \ }\)とおくと
\(\small{ \ t^2-3t-4=0 \ }\)
\(\small{ \ (t-4)(t+1)=0 \ }\)
\(\small{ \ t=4, \ -1 \ }\)
\(\small{ \ \log_2x=4, \ -1 \ }\)
\(\small{ \ x=16, \ \displaystyle\frac{1}{2} \ }\)

Point 対数関数を含む方程式(対数方程式)とその解き方
①真数が一次式になっている場合は\(\small{ \ \log_aA=\log_aB \ }\)の形にまとめる
②(対数)\(\small{ ^2 \ }\)を見たら置換する
次の方程式を解け。
\(\small{ \ x^{\log_2x}=\displaystyle\frac{x^5}{64} \ }\)
\(\small{ \ x^{\log_2x}=\displaystyle\frac{x^5}{64} \ }\)
真数条件より\(\small{ \ x\gt0 \ }\)より両辺ともに正
\(\small{ \ x=1 \ }\)のとき
左辺\(\small{ \ =1 \ }\)、右辺\(\small{ \ =\displaystyle\frac{1}{64} \ }\)より\(\small{ \ x\neq1 \ }\)
\(\small{ \ \therefore x\gt0, \ x\neq1 \ }\)より
両辺に底\(\small{ \ 2 \ }\)とする対数をとると
\(\small{ \ \log_2x^{\log_2x}=\log_2\displaystyle\frac{x^5}{64} \ }\)
\(\small{ \ \left(\log_2x\right)^2=\log_2x^5-\log_264 \ }\)
\(\small{ \ \left(\log_2x\right)^2=5\log_2x-6\ }\)
\(\small{ \ \left(\log_2x\right)^2-5\log_2x+6=0\ }\)
\(\small{ \ \log_2x=t \ }\)とおくと
\(\small{ \ t^2-5t+6=0 \ }\)
\(\small{ \ (t-2)(t-3)=0 \ }\)
\(\small{ \ t=2, \ 3 \ }\)
\(\small{ \ \log_2x=2, \ 3 \ }\)
\(\small{ \ \therefore x=4, \ 8 \ }\)


