二次関数の最大最小（グラフが固定で定義域が一定の間隔のまま動く）

こんにちは、リンス(@Lins016)です。
今回は関数（グラフ）が固定され、定義域が一定の間隔のまま動く二次関数の最大最小について学習していこう。

二次関数の最大値最小値の場合分け問題

今回学習するのは関数が\(\small{ \ y=x^2-2x+3 \ }\)のように定められていて定義域が\(\small{ \ a \leqq x \leqq a+2 \ }\)のように定数（\(\small{ \ a \ }\)）が入っていて定義域の間隔が一定な二次関数の最大最小問題。

つまり「グラフが固定されていて定義域が動く」二次関数の最大最小問題ってことになるんだ。

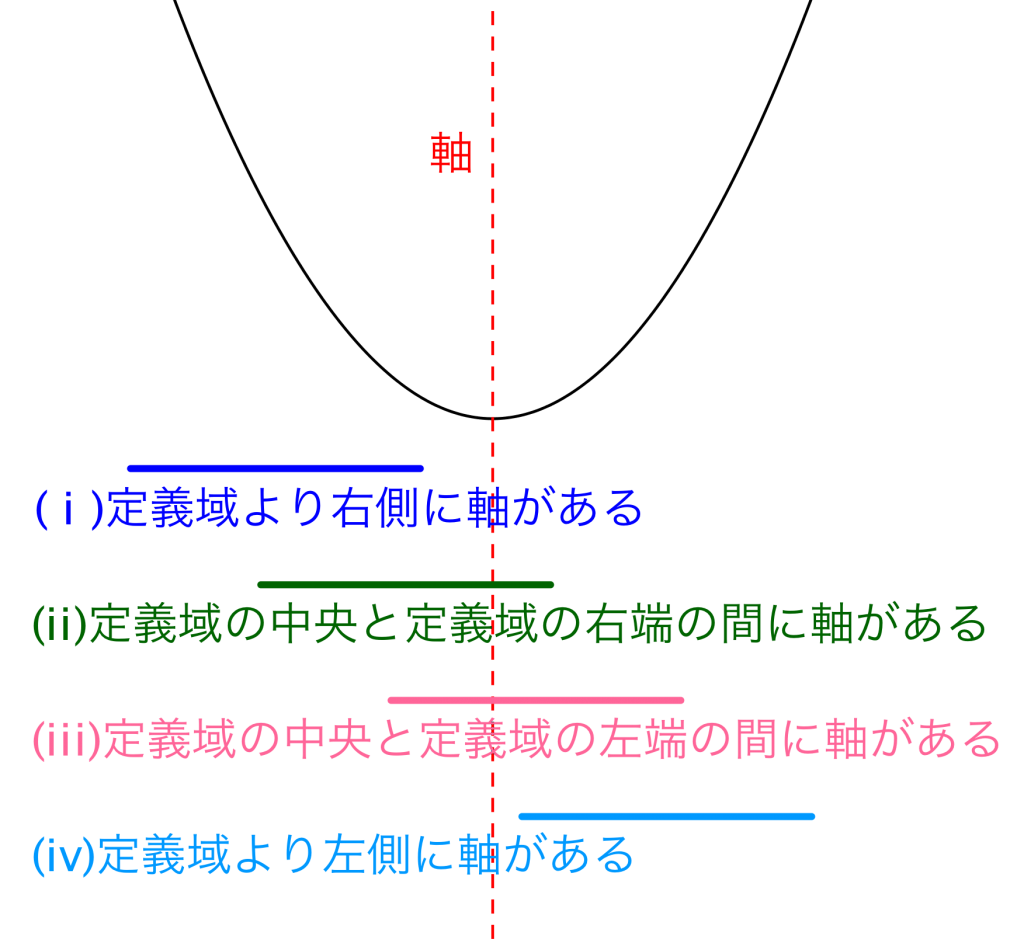
「定義域より右側に軸がある」「定義域の中央と定義域の右端の間に軸がある」「定義域の中央と定義域の左端の間に軸がある」「定義域より左側に軸がある」で最大値や最小値をとる\(\small{ \ x \ }\)の値が変わってくるから、定義域とグラフの軸の位置関係によって定数\(\small{ \ a \ }\)の範囲を場合分けしよう。

まずはグラフと定義域をきちんと書いて場合分けが確実にできるように練習しよう。

「定義域とグラフの軸の位置関係」を定数の範囲によって場合分け

この問題も「定義域が固定されてグラフが動く最大最小」と同じように軸と定義域の位置関係で場合分けをしていこう。

今回は「グラフが固定されて定義域が動く問題」だけど、「定義域が固定されてグラフが動く最大最小問題」とやることは変わらない。

だから、下に凸のグラフの場合、最大値は「定義域の中央より大きい位置に軸がある」「定義域の中央より小さい位置に軸がある」の場合分け、最小値は「定義域の中に軸がある」「定義域より小さい位置に軸がある」「定義域より大きい位置に軸がある」の場合分けになるから、場合分けしていこう。

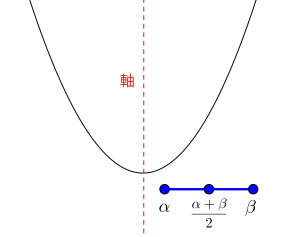
定義域が\(\small{ \ \alpha \leqq x \leqq \beta \ }\)の場合、定義域の中央は\(\small{ \ \displaystyle\frac{\alpha+\beta}{2} \ }\)になるから、次のように場合分けしていこう。

定義域と軸の位置関係

下に凸のグラフで定義域が\(\small{ \ \alpha \leqq x \leqq \beta \ }\)の場合

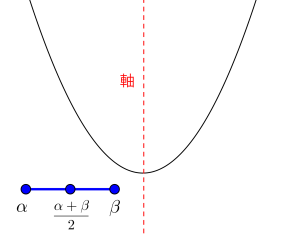
(i)\(\small{ \ \beta \leqq 軸 \ }\)のとき
最大値\(\small{ \ f(\alpha) \ }\)
最小値\(\small{ \ f(\beta) \ }\)

(ii)\(\small{ \ \displaystyle\frac{\alpha+\beta}{2} \leqq 軸 \lt \beta \ }\)のとき
最大値\(\small{ \ f(\alpha) \ }\)
最小値\(\small{ \ f(軸) \ }\)

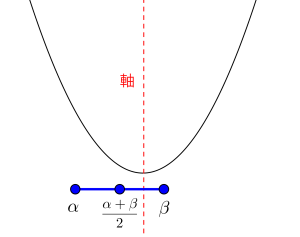
(iii)\(\small{ \ \alpha \leqq 軸 \lt \displaystyle\frac{\alpha+\beta}{2} \ }\)のとき
最大値\(\small{ \ f(\beta) \ }\)
最小値\(\small{ \ f(軸) \ }\)

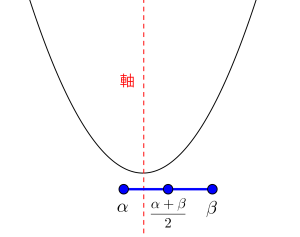
(iv)\(\small{ \ \alpha \gt 軸 \ }\)のとき
最大値\(\small{ \ f(\beta) \ }\)
最小値\(\small{ \ f(\alpha) \ }\)

場合分けは定義域と軸の位置関係だから、\(\small{ \ \beta \leqq 軸 \ }\)、\(\small{ \ \displaystyle\frac{\alpha+\beta}{2} \leqq 軸 \lt \beta \ }\)、\(\small{ \ \alpha \leqq 軸 \lt \displaystyle\frac{\alpha+\beta}{2} \ }\)、\(\small{ \ \alpha \gt 軸 \ }\)を自分で書けるようにならないと意味ないからね。

問題解答

\(\small{ \ a \leqq x \leqq a+1 \ }\)における\(\small{ \ y=x^2-6x+10 \ }\)の最大値と最小値を求めよ。

平方完成すると
\(\small{\begin{eqnarray}
y&=&x^2-6x+10\\
&=&(x-3)^2+1
\end{eqnarray}}\)

(i)\(\small{ \ a+1 \lt 3 \ }\)のとき\(\small{ \ \therefore a \lt 2 \ }\)
グラフより
最大値\(\small{ \ x=a \ }\)のとき\(\small{ \ a^2-6a+10 \ }\)
最小値\(\small{ \ x=a+1 \ }\)のとき\(\small{ \ a^2-4a+5 \ }\)

(ii)\(\small{ \ \displaystyle \frac{2a+1}{2} \lt 3 \leqq a+1 \ }\)のとき
\(\small{ \ \therefore 2\leqq a \lt \displaystyle \frac{5}{2} \ }\)
グラフより
最大値\(\small{ \ x=a \ }\)のとき\(\small{ \ a^2-6a+10 \ }\)
最小値\(\small{ \ x=3 \ }\)のとき\(\small{ \ 1\ }\)

(iii)\(\small{ \ a \lt 3 \leqq \displaystyle \frac{2a+1}{2} \ }\)のとき
\(\small{ \ \therefore \displaystyle\frac{5}{2}\leqq a \lt 3 \ }\)
グラフより
最大値\(\small{ \ x=a+1 \ }\)のとき\(\small{ \ a^2-4a+5 \ }\)
最小値\(\small{ \ x=3 \ }\)のとき\(\small{ \ 1\ }\)

(iv)\(\small{ \ a \geqq 3 \ }\)のとき
グラフより
最大値\(\small{ \ x=a+1 \ }\)のとき\(\small{ \ a^2-4a+5 \ }\)
最大値\(\small{ \ x=a \ }\)のとき\(\small{ \ a^2-6a+10 \ }\)

ここまでに二次関数の最大最小の場合分けについては、全部で3つの形（定義域が固定されグラフが動く・グラフが固定で定義域の一端が動く・グラフが固定で定義域が一定の間隔で動く）を学習してきたけど、やっぱり軸と定義域の位置関係が重要だってことがわかるよね。

常にグラフを書いて定義域を書き込み、定数\(\small{ \ a \ }\)の範囲を場合分けして、最大値と最小値をとる\(\small{ \ x \ }\)の値を求めよう。

Point　二次関数の最大最小（グラフが固定で定義域が一定の間隔のまま動く）

①定義域に対してグラフの軸がどこにあるか、4つのパターン「定義域より右側に軸がある」「定義域の中央と定義域の右端の間に軸がある」「定義域の中央と定義域の左端の間に軸がある」「定義域より左側に軸がある」に場合分けする