こんにちは、リンス(@Lins016)です。
今回は二次不等式の解き方について学習していこう。
二次不等式の解き方
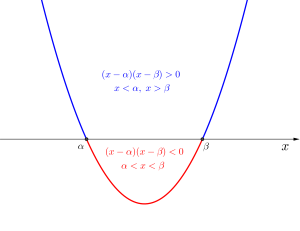
二次不等式の解き方はまず\(\small{ \ x^2\ }\)の係数を正にして下に凸にすることから始めよう。下に凸のグラフと\(\small{ \ x \ }\)軸との交点を調べて大小関係を考えればいいからね。
\(\small{ \ ax^2+bx+c\gt 0 \ }\)
・\(\small{ \ (x-\alpha)(x-\beta)\gt 0 \ }\)のとき
\(\small{ \ x\lt \alpha, \ x \gt \beta \ }\)
・\(\small{ \ (x-\alpha)(x-\beta)\lt 0 \ }\)のとき
\(\small{ \ \alpha \lt x \lt \beta \ }\)
まずは下に凸の形にしよう
下に凸にすることによって\(\small{ \ f(x)\gt0 \ }\)か\(\small{ \ f(x)\lt0 \ }\)のときの答えの形が\(\small{ \ f(x)\gt0 \ }\)なら\(\small{ \ x\lt \alpha, \ x \gt \beta \ }\)の二つに分かれる形だし、\(\small{ \ f(x)\lt0 \ }\)なら\(\small{ \ \alpha \lt x \lt \beta \ }\)のはさまれる形になるから、常に下に凸の形にしてから考えよう。上に凸も考えると\(\small{ \ f(x)\gt0 \ }\)なら\(\small{ \ x\lt \alpha, \ x \gt \beta \ }\)の形みたいにできなくなるからね。ただ不等式の両辺にマイナスをかけると不等号の向きが変わることに注意しておこう。
接するときは特に注意しよう
\(\small{ \ (x-a)^2\geqq0 \ }\)なら\(\small{ \ x \ }\)はすべての実数になるけど、\(\small{ \ (x-a)^2\gt0 \ }\)なら\(\small{ \ x \ }\)は\(\small{ \ a \ }\)以外の実数になる。\(\small{ \ (x-a)^2\leqq0 \ }\)なら\(\small{ \ x=a \ }\)だけど、\(\small{ \ (x-a)^2\lt0 \ }\)なら解なしになるからね。これはグラフと\(\small{ \ x \ }\)軸の関係から考えて答えを出さないといけないね。接する場合は注意して答えをだそう。

次の二次不等式を解け。
(1)\(\small{ \ x^2-3x+2\lt0 \ }\)
(2)\(\small{ \ x^2-9\gt0 \ }\)
(3)\(\small{ \ x^2-4x+4 \gt 0 \ }\)
(4)\(\small{ \ x^2-3x-1\lt0 \ }\)
(1)\(\small{ \ x^2-3x+2\lt0 \ }\)
\(\small{ \ (x-2)(x-1)\lt0 \ }\)
\(\small{ \ 1\lt x \lt 2 \ }\)
(2)\(\small{ \ x^2-9\gt0 \ }\)
\(\small{ \ (x-3)(x+3)\gt0 \ }\)
\(\small{ \ x\lt-3, \ x\gt3 \ }\)
(3)\(\small{ \ x^2-4x+4 \gt 0 \ }\)
\(\small{ \ (x-2)^2\gt0 \ }\)
\(\small{ \ x\neq2 \ }\)
(4)\(\small{ \ x^2-3x-1\lt0 \ }\)
\(\small{ \ x^2-3x-1=0 \ }\)とすると
\(\small{ \ x=\displaystyle \frac{3\pm\sqrt{13}}{2} \ }\)より
\(\small{ \ \displaystyle \frac{3-\sqrt{13}}{2} \lt x \lt \displaystyle \frac{3+\sqrt{13}}{2} \ }\)

Point
①まずは下に凸に変形しよう
②因数分解できなかったら解の公式を利用しよう
\(\small{ \ x \ }\)についての2次不等式\(\small{ \ x^2-(a+1)x+a \lt0 \ }\)と\(\small{ \ 3x^2+2x-1\gt0 \ }\)を同時に満たす整数\(\small{ \ x \ }\)がちょうど\(\small{ \ 3 \ }\)個存在するような定数\(\small{ \ a \ }\)の範囲を求めよ。
\(\small{ \ 3x^2+2x-1\gt 0 \ }\)
\(\small{ \ (3x-1)(x+1)\gt0 \ }\)
\(\small{ \ x\lt -1, \ x\gt \displaystyle \frac {1}{3} \ }\)
\(\small{ \ x^2-(a+1)x+a \lt0 \ }\)
\(\small{ \ (x-1)(x-a)\lt0 \ }\)
(i)\(\small{ \ a \gt 1 \ }\)のとき\(\small{ \ 1\lt x \lt a \ }\)
(ii)\(\small{ \ a=1 \ }\)のとき解なし
(iii)\(\small{ \ a\lt 1 \ }\)のとき\(\small{ \ a \lt x \lt 1 \ }\)
2つの式を同時に満たす整数\(\small{ \ x \ }\)がちょうど3つになるときを考える。
(ア)\(\small{ \ a \gt 1 \ }\)のとき
整数解は\(\small{ \ x=2, \ 3, \ 4 \ }\)になるので、
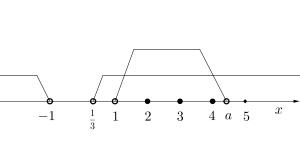
\(\small{ \ 4 \lt a \leqq 5 \ }\)
(イ)\(\small{ \ a \lt 1 \ }\)のとき
整数解は \(\small{ \ x=-2, \ -3, \ -4 \ }\)になるので、
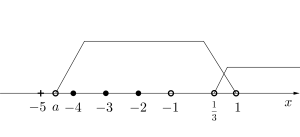
\(\small{ \ -5\leqq a \lt -4 \ }\)

ちなみにこの問題文の不等式が\(\small{ \ x^2-(a+1)x+a \lt0 \ }\)と\(\small{ \ x^2-(a+1)x+a \leqq 0 \ }\)で答えも変わってくるから数直線を書いて端を含む、含まないに注意して答えを書こう。

