こんにちは、リンス(@Lins016)です。
今回は判別式とその利用について学習していこう。
判別式とは
二次方程式\(\small{ \ ax^2+bx+c=0 \ }\)は解を\(\small{ \ 2 \ }\)つ持つ場合もあれば、重解になる場合もあるし、解なしの場合もあるよね。これを考えるのが判別式なんだ。
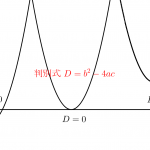
『\(\small{ \ ax^2+bx+c=0 \ }\)の判別式は\(\small{ \ D=b^2-4ac \ }\)』でこの値によって解の個数が変わっていく。
判別式は英語でdiscriminantって言うからこの頭文字をとって一般的に記号\(\small{ \ D \ }\)が使われてるんだ。
ちなみにこの数学Ⅰの二次関数の単元では実数の範囲しか取り扱わないけど、数学Ⅱの複素数と方程式では虚数(\(\small{ \ 2 \ }\)乗して\(\small{ \ -1 \ }\)になる数)の範囲も取り扱うから少し内容が変わるからね。
虚数も考える場合の判別式が知りたい場合は下のベージを確認しておこう。
-

二次方程式と判別式
複素数の範囲まで考えた二次方程式と判別式について詳しく解説しています。
続きを見る
・\(\small{ \ ax^2+bx+c=0 \ }\)の解の個数を調べる
判別式\(\small{ \ D=b^2-4ac \ }\)
\(\small{ \ D\gt0 \ }\)のとき実数解\(\small{ \ 2 \ }\)個
\(\small{ \ D=0 \ }\)のとき重解
\(\small{ \ D\lt0 \ }\)のとき実数解なし
判別式と解の公式
まずはじめに\(\small{ \ ax^2+bx+c=0 \ }\)の二次方程式の解は解の公式を使うと\(\small{ \ x=\displaystyle \frac{-b\pm\sqrt{b^2-4ac}}{2a} \ }\)だったよね。
判別式\(\small{ \ D \ }\)はこの解の公式の根号内の\(\small{ \ b^2-4ac \ }\)になるんだ。
だから\(\small{ \ ax^2+bx+c=0 \ }\)の解は\(\small{ \ x=\displaystyle \frac{-b\pm\sqrt{D}}{2a} \ }\)って書くことができるから覚えておこう。
二次方程式の解の個数
判別式は二次方程式が解を持つか持たないか、解の個数を調べるために利用するんだ。
\(\small{ \ ax^2+bx+c=0 \ }\)の判別式\(\small{ \ D=b^2-4ac \ }\)は、この方程式の解の\(\small{ \ x=\displaystyle \frac{-b\pm\sqrt{D}}{2a} \ }\)の根号の中を示すから、根号の中が正の値だと根号の前に\(\small{ \ \pm \ }\)の記号があるから解を\(\small{ \ 2 \ }\)つ持つし、\(\small{ \ D=0 \ }\)なら解は\(\small{ \ x=-\displaystyle \frac{b}{2a} \ }\)になって重解になるし、\(\small{ \ D\lt0 \ }\)なら根号の中が負になるから実数にならない、つまり解なしになるよね。
だから\(\small{ \ ax^2+bx+c=0 \ }\)の二次方程式の解ついて判別式で実数解の個数が分かるんだ。
判別式DとD/4
\(\small{ \ ax^2+bx+c=0 \ }\)の\(\small{ \ b \ }\)が偶数のとき、判別式の計算を少し工夫することができる。
\(\small{ \ b=2b' \ }\)とすると\(\small{ \ ax^2+2b'x+c=0 \ }\)ってなるから、\(\small{ \ D=4b'^2-4ac \ }\)になるよね。これを\(\small{ \ 4 \ }\)で割ると\(\small{ \ \displaystyle\frac{D}{4}=b'^2-ac \ }\)になるんだけど、この判別式\(\small{ \ \displaystyle\frac{D}{4} \ }\)と\(\small{ \ D \ }\)の符号は同じだよね。
つまり\(\small{ \ D\gt0 \ }\)なら\(\small{ \ \displaystyle\frac{D}{4}\gt0 \ }\)だし、\(\small{ \ D=0 \ }\)なら\(\small{ \ \displaystyle\frac{D}{4}=0 \ }\)だし、\(\small{ \ D\lt0 \ }\)なら\(\small{ \ \displaystyle\frac{D}{4}\lt0 \ }\)が言えるよね。
だから\(\small{ \ ax^2+bx+c=0 \ }\)の\(\small{ \ b \ }\)が偶数のとき判別式を使う場合は\(\small{ \ D \ }\)より\(\small{ \ \displaystyle\frac{D}{4} \ }\)の方が計算が楽になるんだ。
判別式を使う時に\(\small{ \ b \ }\)が偶数なら絶対\(\small{ \ \displaystyle\frac{D}{4} \ }\)を使わないといけないってことはないから\(\small{ \ D \ }\)を使っても問題ないんだけど、\(\small{ \ b \ }\)が大きい数なら計算がだいぶ楽になるから覚えておこう。
二次関数と\(\small{ \ x \ }\)軸との共有点の個数
今度は判別式を\(\small{ \ y=ax^2+bx+c \ }\)と\(\small{ \ y=0 \ }\)との共有点の個数に利用してみよう。
\(\small{ \ y=ax^2+bx+c \ }\)と\(\small{ \ y=0 \ }\)の共有点の\(\small{ \ x \ }\)座標はこの\(\small{ \ 2 \ }\)つの式を結んだ\(\small{ \ ax^2+bx+c=0 \ }\)を解いた値になるから、判別式によって二次関数のグラフと\(\small{ \ x \ }\)軸との共有点の数がわかることになるよね。
だから二次関数のグラフが\(\small{ \ x \ }\)軸と交わるかどうかを調べるときは判別式を使おう。
ちなみに\(\small{ \ y=ax^2+bx+c=a\left(x+\displaystyle \frac{b}{2a}\right)^2-\displaystyle \frac{b^2-4ac}{4a} \ }\)になるから、グラフの凸の向きと頂点の\(\small{ \ y \ }\)座標でも交点の数が分かるよね。
頂点の\(\small{ \ y \ }\)座標は\(\small{ \ -\displaystyle \frac{b^2-4ac}{4a} \ }\)だから判別式で\(\small{ \ x \ }\)軸との共有点の数を求めることと、放物線の頂点の座標から\(\small{ \ x \ }\)軸との共有点の数を求めることは同じことだから覚えておこう。
(1)次の方程式の実数解の個数を求めよ。
\(\small{ \ ax^2+x+1=0 \ }\)
(2)次の\(\small{ \ 2 \ }\)次方程式が重解を持つように定数\(\small{ \ k \ }\)を定めよ。またそのときの解も求めよ。
\(\small{ \ 4x^2+(k-2)x+1=0 \ }\)
(1)\(\small{ \ a=0 \ }\)のとき
\(\small{ \ x+1=0 \ }\)より、実数解1個
\(\small{ \ a \neq 0 \ }\)のとき
\(\small{ \ D=1-4a \ }\)より
\(\small{ \ D=1-4a\gt0 \ \therefore a\lt0, \ 0\lt a\lt \displaystyle \frac{1}{4}}\)のとき実数解\(\small{ \ 2 \ }\)個
\(\small{ \ D=1-4a=0 \ \therefore a=\displaystyle \frac{1}{4}}\)のとき重解
\(\small{ \ D=1-4a\lt0 \ \therefore a\gt \displaystyle \frac{1}{4}}\)のとき実数解なし
(2)\(\small{ \ D=(k-2)^2-16 \ }\)より
\(\small{ \ k^2-4k-12=0 \ }\)
\(\small{ \ (k+2)(k-6)=0 \ }\)
\(\small{ \ k=-2, \ 6 \ }\)
\(\small{ \ k=-2 \ }\)のとき
\(\small{ \ (2x-1)^2=0 \ }\)
\(\small{ \ \therefore x=\displaystyle \frac{1}{2} \ }\)
\(\small{ \ k=6 \ }\)のとき
\(\small{ \ (2x+1)^2=0 \ }\)
\(\small{ \ \therefore x=-\displaystyle \frac{1}{2} \ }\)

Point 判別式とその利用
①二次方程式が解を持つ条件は\(\small{ \ D\geqq0 \ }\)になる
②二次関数のグラフと\(\small{ \ x \ }\)軸との交点を求めるとき、判別式と頂点の\(\small{ \ y \ }\)座標の位置を調べるのは同じこと
次の関数の最大値と最小値を求めよ。
\(\small{ \ y=\displaystyle \frac{x}{x^2+1} \ }\)
\(\small{ \ y=\displaystyle \frac{x}{x^2+1} \ }\)
\(\small{ \ y(x^2+1)=x \ }\)
\(\small{ \ yx^2 -x+y=0\ }\)
この2次方程式の解が存在するので、
\(\small{ \ D=(-1)^2-4y^2\geqq0 \ }\)
\(\small{ \ \therefore -\displaystyle \frac{1}{2}\leqq y \leqq \displaystyle \frac{1}{2} \ }\)
よって最大値\(\small{ \ \displaystyle \frac{1}{2} \ }\)
最小値\(\small{ \ -\displaystyle \frac{1}{2} \ }\)

つまり不等式を作るってことは[ ]\(\small{ \ \leqq k \leqq \ }\)[ ]のような形や\(\small{ \ k \geqq \ }\)[ ]のような形が作れることになる。
だから、\(\small{ \ k \ }\)の最大値・最小値を求めるためにも使うこともできるよね。
文系の生徒は分数関数の最大最小を微分して求めることが出来ないから、この解法は必ずマスターしておこう。