こんにちは、リンス(@Lins016)です。
今回は放物線が切り取る線分の長さについて学習していこう。
放物線が切り取る線分の長さ
放物線が\(\small{ \ x \ }\)軸と異なる2つの点で交わるとき、その2点を結ぶ線分の長さを求めてみよう。
\(\small{ \ f(x)=ax^2+bx+c=0 \ }\)
\(\small{ \ x=\displaystyle \frac{-b\pm\sqrt{b^2-4ac}}{2a} \ }\)
①\(\small{ \ a\gt0 \ }\)のとき
\(\small{ \ \displaystyle \frac{-b+\sqrt{D}}{2a}-\displaystyle \frac{-b-\sqrt{D}}{2a}=\displaystyle \frac{\sqrt{D}}{a} \ }\)
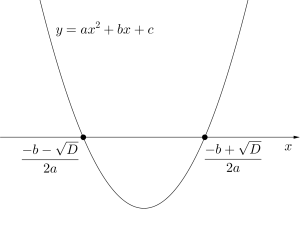
②\(\small{ \ a\lt0 \ }\)のとき
\(\small{ \ \displaystyle \frac{-b-\sqrt{D}}{2a}-\displaystyle \frac{-b+\sqrt{D}}{2a}=-\displaystyle \frac{\sqrt{D}}{a} \ }\)
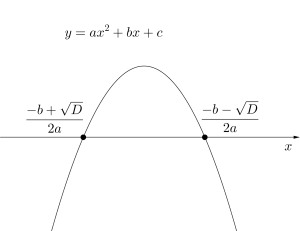
①②より\(\small{ \ a \ }\)の符号に関わらず\(\small{ \ x \ }\)軸を切り取る線分の長さは\(\small{ \ \displaystyle \frac{\sqrt{D}}{|a|} \ }\)
解の公式でも解と係数の関係でも導ける
\(\small{ \ x \ }\)軸を切り取る線分の長さは、解の公式から\(\small{ \ x \ }\)軸との交点の座標を求めて大きい座標から小さい座標を引けばいいよね。
すると上にも書いてあるように切り取る線分の長さは\(\small{ \ \displaystyle \frac{\sqrt{D}}{|a|} \ }\)になる。
これを解と係数の関係を利用して解いてみよう。
\(\small{ \ ax^2+bx+c=0 \ }\)の解を\(\small{ \ x=\alpha, \ \beta \ }\)とすると、切り取る線分の長さは\(\small{ \ \beta-\alpha \ (\alpha\lt \beta) \ }\)になるよね。
ここで解と係数の関係を利用すると
\(\small{ \begin{eqnarray}\ \beta-\alpha&=&\sqrt{(\alpha+\beta)^2-4\alpha\beta}\\[6pt]
&=&\sqrt{\left(-\displaystyle \frac{b}{a}\right)^2-4\displaystyle \frac{c}{a}}\\[6pt]
&=&\sqrt{\displaystyle \frac{b^2-4ac}{a^2}}\\[6pt]
&=&\displaystyle \frac{\sqrt{D}}{|a|} \ \end{eqnarray}}\)
ってなるから解の公式を利用した場合と同じになる。
どちらも同じことを考えてるわけだから一緒になるに決まっているよね。
解と係数の関係で解く必要は特別なかったんだけど、解と係数の関係でも解けるんだよってことと、解と係数の関係を忘れてないかなって確認も踏まえて解いてみたんだ。
忘れていたらきちんと確認しておこう。本当に重要な公式だからね。
とにかく切り取る線分の長さは\(\small{ \ \displaystyle \frac{\sqrt{D}}{|a|} \ }\)って覚えておこう。
-

解と係数の関係の証明
二次方程式と三次方程式の解と係数の関係の証明について詳しく解説しています。
続きを見る
(1)2次関数\(\small{ \ y=x^2-5x-14 \ }\)のグラフが\(\small{ \ x \ }\)軸から切り取る線分の長さを求めよ。
(2)2次関数\(\small{ \ y=x^2-x \ }\)が直線\(\small{ \ y=2x+1 \ }\)を切り取る線分の長さを求めよ。
(1)\(\small{ \ x^2-5x-14=0 \ }\)
\(\small{ \ (x-7)(x+2)=0 \ }\)
\(\small{ \ x=7, \ -2 \ }\)
よって切り取る線分の長さは\(\small{ \ 7-(-2)=9 \ }\)
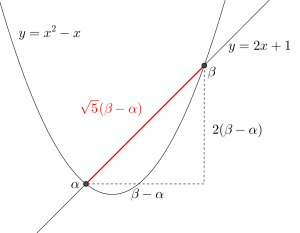
(2)2次関数\(\small{ \ y=x^2-x \ }\)と直線\(\small{ \ y=2x+1 \ }\)の交点の\(\small{ \ x \ }\)座標は
\(\small{ \ x^2-x=2x+1 \ }\)
\(\small{ \ x^2-3x-1=0 \ }\)
\(\small{ \ x=\displaystyle \frac{3\pm\sqrt{13}}{2} \ }\)
直線の傾きは\(\small{ \ 2 \ }\)より求める線分の長さは
\(\small{ \ \sqrt{5}\cdot \left(\displaystyle \frac{3+\sqrt{13}}{2}-\displaystyle \frac{3-\sqrt{13}}{2}\right)\\
=\sqrt{65} \ }\)

傾き\(\small{ \ m \ }\)の直線は\(\small{ \ x \ }\)軸方向に\(\small{ \ 1 \ }\)進んだとき、\(\small{ \ y \ }\)軸方向に\(\small{ \ m \ }\)上がる直線だから、三平方の定理から斜めの距離は\(\small{ \ \sqrt{m^2+1} \ }\)ってことになるよね。
これを利用して斜めの直線を切り取る線分の長さは、三平方の定理から求めるんじゃなくて、\(\small{ \ x \ }\)座標の差を\(\small{ \ \sqrt{m^2+1} \ }\)倍して求めよう。
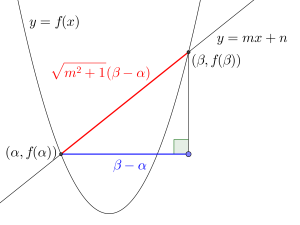
-

円が切り取る線分(弦)の長さ
点と直線の距離を利用した解法や解と係数の関係を利用した解法について詳しく解説しています。
続きを見る
Point
①放物線が切り取る\(\small{ \ x \ }\)軸の線分の長さは\(\small{ \ \displaystyle \frac{\sqrt{D}}{|a|} \ }\)
②放物線が直線を切り取る線分の長さは\(\small{ \ \sqrt{(傾き)^2+1}(\beta-\alpha) \ }\)を利用しよう


