二次関数と二次方程式と二次不等式【二次式まとめ】

こんにちは、リンス(@Lins016)です。
今回は二次関数と二次方程式と二次不等式(二次式のまとめ)について学習していこう。

今回の学習は二次関数を苦手にしている人向けになるから、理解してる人はさらっと読み流しても大丈夫。苦手にしている人はきちんと読んで下のような間違いをしていないか考えてみよう。

二次関数と二次方程式と二次不等式

二次関数と二次方程式と二次不等式はどれも\(\small{ \ ax^2+bx+c \ }\)を利用するんだけど、変形する形が違うから注意しよう。

二次関数は最大値や最小値が知りたいから平方完成するのが基本。

それに対して、二次方程式や不等式は二次式が\(\small{ \ 0 \ }\)になる\(\small{ \ x \ }\)の値を利用するから、因数分解や解の公式を利用するからね。

\(\small{ \ ax^2+bx+c \ }\)が\(\small{ \ y=ax^2+bx+c \ }\)なら二次関数、\(\small{ \ ax^2+bx+c=0 \ }\)なら二次方程式、\(\small{ \ ax^2+bx+c\leqq0 \ }\)なら二次不等式だから、最大値や最小値が知りたいのに因数分解したり、方程式を解きたいのに平方完成したり、因数分解と平方完成の使い方を逆にしたことある人はもう一度基本に戻って学習しておこう。

二次式まとめ

・二次関数
\(\small{ \ y=ax^2+bx+c \ }\)の場合
\(\small{ \ y=a(x-p)^2+q \ }\)に変形

・二次方程式
\(\small{ \ ax^2+bx+c=0 \ }\)の場合
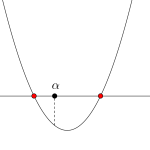
\(\small{ \ a(x-\alpha)(x-\beta)=0 \ }\)より\(\small{ \ x=\alpha, \ \beta \ }\)

・二次不等式
\(\small{ \ ax^2+bx+c\geqq 0 \ }\)の場合
\(\small{ \ a(x-\alpha)(x-\beta)\geqq 0 \ }\)より\(\small{ \ x \leqq \alpha, \ x \geqq \beta \ }\)

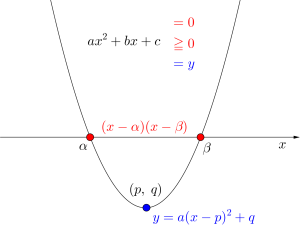
二次関数と平方完成

高校数学の関数の基本は「\(\small{ \ x \ }\)の値が変化するとき、\(\small{ \ y \ }\)の値がどう変化するか」を考えるものだよね。

\(\small{ \ x \ }\)の範囲（定義域）や\(\small{ \ y \ }\)の範囲（値域または最大値・最小値）を考えるのが関数だから二次、二次関数のグラフ全体を確認する必要があるよね。

だからグラフの頂点や軸を調べる必要があるんだ。むしろ\(\small{ \ x \ }\)軸との共有点の座標はそんなに重要じゃない。

グラフの頂点や軸を調べるために平方完成する。つまり二次関数って言われたら\(\small{ \ y=ax^2+bx+c \ }\)を\(\small{ \ y=a(x-p)^2+q \ }\)の形に変形しよう。

二次方程式・二次不等式と因数分解・解の公式

二次関数の平方完成に対して、二次方程式や二次不等式は\(\small{ \ ax^2+bx+c \ }\)のグラフが\(\small{ \ x \ }\)軸との共有点の座標が必要になるよね。この共有点の座標は平方完成じゃ求められない。。。（厳密には平方完成を利用して求められないわけじゃないけど、高校生はそんな解き方しないからね。）

この共有点を求めるためには\(\small{ \ ax^2+bx+c=0 \ }\)を因数分解、因数分解できなかったら解の公式で共有点を求めよう。

平方完成と因数分解が混乱する原因

二次方程式・二次不等式なら\(\small{ \ 2x^2+4x-6=0 \ }\)を\(\small{ \ 2 \ }\)で割って\(\small{ \ x^2+2x-3=0 \ }\)ってしてもいいんだけど、\(\small{ \ y=2x^2+4x-6 \ }\)を\(\small{ \ 2 \ }\)で割って\(\small{ \ y=x^2+2x-3 \ }\)ってすると関数が違う関数になるから絶対割ったらダメなんだ。

最大値や最小値も\(\small{ \ 2 \ }\)で割られることなるからね。

でも二次方程式・二次不等式なら\(\small{ \ 2x^2+4x-6=0 \ }\)は必ず\(\small{ \ 2 \ }\)で割って\(\small{ \ x^2+2x-3=0 \ }\)にしてから解いてほしい。計算量が減るし、因数分解も格段にやりやすくなるからね。

問題を解く上で少しでもミスをなくすようにしたいよね。だから計算量を減らす工夫をしないとね。

二次方程式・二次不等式なら因数分解するにしても、解の公式を使うにしても各係数に共通因数があるならその共通因数で割ろう。

解の存在範囲で混乱する？

解の存在範囲は二次方程式の問題だけど、二次関数のグラフの位置を利用して考えることがある。

二次関数を解いてるのか二次方程式を解いているのか、わかりにくくなるよね。

確かに二次方程式の問題だから解の公式を利用して考えれば良さそうだけど、それだと答えを出すのがすごく大変。だからグラフを利用して考えるんだ。

解の公式を利用して答えるのが大変だってことをきちんと理解して、最大最小を求める二次関数と、\(\small{ \ x \ }\)軸との交点の値を求める二次方程式の違いをきちんと確認しておこう。

判別式の利用で混乱する？

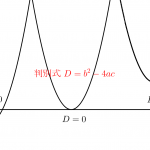
判別式は方程式で利用すれば解を持つ・持たないってことになるけど、二次関数で利用すれば、放物線と直線が交わる・交わらないってことになるよね。これもきちんと理解できていない人には混乱する原因の一つだと思う。

交点の座標は二次方程式を解いて求めるからね。

自分がやりたいことをきちんとできるように各パターンの解法をきちんとチェックしておこう。解法があやふやのままだと間違った形に変形してしまうからね。
・二次方程式の解き方
・二次不等式の解き方
・二次関数のグラフと平方完成

Point 二次式まとめ

①二次関数は平方完成を利用
②二次方程式・不等式は因数分解か解の公式を利用