こんにちは、リンス(@Lins016)です。
今回は定義域が固定されグラフが動く二次関数について学習していこう。
二次関数の最大値最小値の場合分け問題
今回学習するのは定義域が\(\small{ \ 1\leqq x \leqq3 \ }\)のように定められていて関数が\(\small{ \ y=x^2-2ax+3 \ }\)のような頂点の\(\small{ \ x \ }\)座標に定数\(\small{ \ a \ }\)が入っているような関数の最大値最小値を求める問題になる。
この形の問題は頂点の\(\small{ \ x \ }\)座標、つまりグラフの軸が定義域に対してどの位置にあるかで最大値や最小値をとる\(\small{ \ x \ }\)の値が変わってくるから、グラフの軸のある位置を定数\(\small{ \ a \ }\)の範囲によって場合分けする必要があるんだ。
ちなみにこの問題は他の単元でも出題されることが多いから、理解できるまで何度もグラフを書いて練習していこう。
下に凸のグラフで定義域が\(\small{ \ \alpha \leqq x \leqq \beta \ }\)の場合の場合分けのパターン
・最大値
①「グラフの軸が定義域の中央より大きい位置にある」
②「グラフの軸が定義域の中央より小さい位置にある」
・最小値
①「グラフの軸が定義域の中にある」
②「グラフの軸が定義域より大きい位置にある」
③「グラフの軸が定義域より小さい位置にある」

上に凸のグラフの場合はこの逆になるから、最小値が「グラフの軸が定義域の中央より大きい位置にある」「グラフの軸が定義域の中央より小さい位置にある」の場合分けになるからね。
だから最大値は「グラフの軸が定義域の中にある」「グラフの軸が定義域より大きい位置にある」「グラフの軸が定義域より小さい位置にある」の場合分けになるから注意しよう。
定義域とグラフの軸との位置関係を定数の値で場合分け
定数\(\small{ \ a \ }\)などが関数に入っているとグラフが定数の値によって移動するよね。
定数\(\small{ \ a \ }\)などが関数に定義域(\(\small{ \ \alpha \leqq x \leqq \beta \ }\))が存在する二次関数の最大最小問題は、グラフの軸と定義域の位置関係で最大値や最小値をとる\(\small{ \ x \ }\)の値が変わってくるんだ。
下に凸の場合、最大値は「グラフの軸が定義域の中央より大きい位置にある」「グラフの軸が定義域の中央より小さい位置にある」で最大値をとる\(\small{ \ x \ }\)の値が変わるし、最小値は「グラフの軸が定義域の中にある」「グラフの軸が定義域より大きい位置にある」「グラフの軸が定義域より小さい位置にある」で最小値をとる\(\small{ \ x \ }\)の値が変わるんだ。
このグラフの軸と定義域の位置関係から定数の範囲を求めて、その範囲によって場合分けしていこう。
\(\small{ \ 0\leqq x \leqq 2 \ }\)における\(\small{ \ y=x^2-4ax+4a^2+1 \ }\)の最大値と最小値を求めよ。
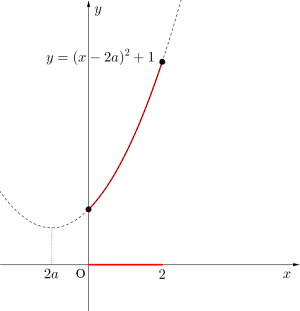
(1)\(\small{ \ 2a \lt 0 \ }\)のとき\(\small{ \ \therefore a \lt 0 \ }\)のとき
グラフより
最大値\(\small{ \ x=2 \ }\)のとき\(\small{ \ 4a^2-8a+5 \ }\)
最小値\(\small{ \ x=0 \ }\)のとき\(\small{ \ 4a^2+1 \ }\)
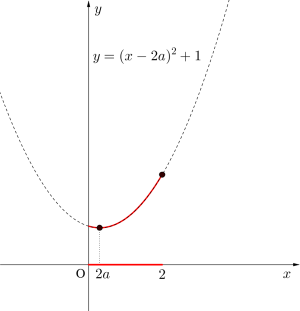
(2)\(\small{ \ 0 \leqq 2a \lt 1 \ }\)のとき\(\small{ \ \therefore 0 \leqq a \lt \displaystyle \frac{1}{2} \ }\)のとき
グラフより
最大値\(\small{ \ x=2 \ }\)のとき\(\small{ \ 4a^2-8a+5 \ }\)
最小値\(\small{ \ x=2a \ }\)のとき\(\small{ \ 1 \ }\)
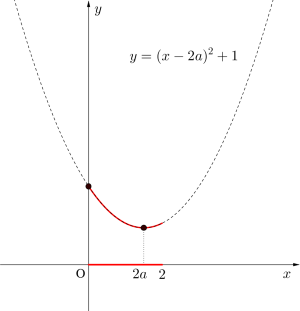
(3)\(\small{ \ 1 \leqq 2a \lt 2 \ }\)のとき\(\small{ \ \therefore \displaystyle \frac{1}{2} \leqq a \lt 1 \ }\)のとき
グラフより
最大値\(\small{ \ x=0 \ }\)のとき\(\small{ \ 4a^2+1 \ }\)
最小値\(\small{ \ x=2a \ }\)のとき\(\small{ \ 1 \ }\)
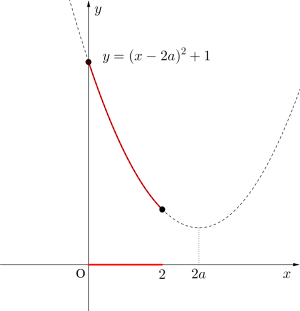
(4)\(\small{ \ 2a \geqq 2 \ }\)のとき\(\small{ \ \therefore a \geqq 1 \ }\)のとき
グラフより
最大値\(\small{ \ x=0 \ }\)のとき\(\small{ \ 4a^2+1 \ }\)
最小値\(\small{ \ x=2 \ }\)のとき\(\small{ \ 4a^2-8a+5 \ }\)

グラフの軸と定義域の位置関係から最大値最小値をとるときの\(\small{ \ x \ }\)の値を求めるのは、グラフが動く場合分けの問題でも動かない問題でも同じだから常に平方完成して軸と定義域の位置関係を確認しよう。
確認するためには、グラフを書くとより正確に答えを導けるから、ざっとしたグラフでも構わないからグラフを書くことも練習しておこう。
Point 二次関数の最大最小(定義域が固定されグラフが動く)
①グラフの軸が定義域のどの位置にあるかで定数を場合分けする
\(\small{ \ a \ }\)を実数とするとき、\(\small{ \ f(x)=x^2-a|x-2|+\displaystyle \frac{a^2}{4} \ }\)の最小値を\(\small{ \ a \ }\)を用いて表せ。
(i)\(\small{ \ x\leqq2 \ }\)のとき
\(\small{\begin{eqnarray} \ f(x)&=&x^2+a(x-2)+\displaystyle \frac{a^2}{4} \\
&=&\left(x+\displaystyle \frac{a}{2}\right)^2-2a \end{eqnarray}}\)
定義域は\(\small{ \ x\leqq2 \ }\)、軸の方程式は\(\small{ \ x=-\displaystyle \frac{a}{2} \ }\)より
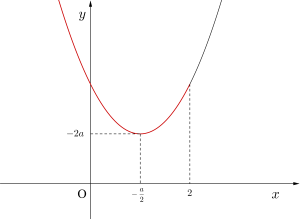
①\(\small{ \ -\displaystyle \frac{a}{2}\leqq 2 \ }\)のとき\(\small{ \ \therefore a\geqq-4 \ }\)のとき
最小値は\(\small{ \ x=-\displaystyle \frac{a}{2} \ }\)のとき\(\small{ \ -2a \ }\)
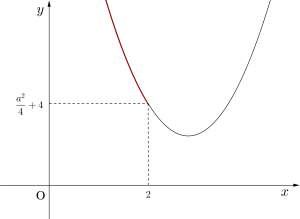
②\(\small{ \ -\displaystyle \frac{a}{2}\gt 2 \ }\)のとき\(\small{ \ \therefore a\lt-4 \ }\)のとき
最小値は\(\small{ \ x=2\ }\)のとき\(\small{ \ \displaystyle \frac{a^2}{4}+4 \ }\)
(ii)\(\small{ \ x\geqq 2 \ }\)のとき
\(\small{ \begin{eqnarray}\ f(x)&=&x^2-a(x-2)+\displaystyle \frac{a^2}{4} \\
&=&\left(x-\displaystyle \frac{a}{2}\right)^2-2a \end{eqnarray}}\)
定義域は\(\small{ \ x\geqq2 \ }\)、軸の方程式は\(\small{ \ x=\displaystyle \frac{a}{2} \ }\)より
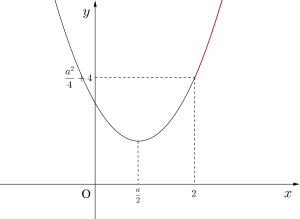
①\(\small{ \ \displaystyle \frac{a}{2}\leqq 2 \ }\)のとき\(\small{ \ \therefore a\leqq 4 \ }\)のとき
最小値は\(\small{ \ x=2 \ }\)のとき\(\small{ \ \displaystyle \frac{a^2}{4}+4 \ }\)
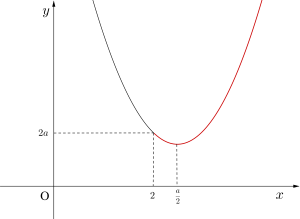
②\(\small{ \ \displaystyle \frac{a}{2}\gt 2 \ }\)のとき\(\small{ \ \therefore a\gt 4 \ }\)のとき
最小値は\(\small{ \ x=\displaystyle \frac{a}{2}\ }\)のとき\(\small{ \ 2a \ }\)
(i)(ii)の最小値を\(\small{ \ a \ }\)の値によって比較すると
ア)\(\small{ \ a\lt -4 \ }\)のとき
最小値は\(\small{ \ \displaystyle \frac{a^2}{4}+4 \ }\)
イ)\(\small{ \ -4 \leqq a\leqq 4 \ }\)のとき
最小値は\(\small{ \ \displaystyle \frac{a^2}{4}+4 \ }\)か\(\small{ \ -2a \ }\)
ここで\(\small{ \ \displaystyle \frac{a^2}{4}+4-(-2a)=\left(\displaystyle \frac{a}{2}+2\right)^2\geqq 0 \ }\)より
\(\small{ \ \displaystyle \frac{a^2}{4}\geqq -2a \ }\)
よって最小値は\(\small{ \ -2a \ }\)
ウ)\(\small{ \ a\gt4 \ }\)のとき
最小値は\(\small{ \ -2a \ }\)か\(\small{ \ 2a \ }\)
\(\small{ \ a\gt4 \ }\)より
最小値は\(\small{ \ -2a \ }\)
よって求める最小値は
\(\small{ \ a\lt -4 \ }\)のとき\(\small{ \ \displaystyle \frac{a^2}{4}+4 \ }\)
\(\small{ \ a\geqq -4 \ }\)のとき\(\small{ \ -2a \ }\)

