こんにちは、リンス(@Lins016)です。
今回は指数関数を含む不等式の解き方について学習していこう。
指数関数を含む不等式の解き方
指数関数を含む不等式を解く場合、指数関数を含む方程式の解き方と同じで、いきなり\(\small{ \ x\gt3 \ }\)みたいに答えが出るわけじゃない。
まずは\(\small{ \ 2^x\gt8 \ }\)っていうのが求まってから\(\small{ \ x\gt3 \ }\)って答えが求まる。まずはこのことを頭に入れておこう。
①\(\small{ \ a^x\leqq a^p \ }\)
(i)\(\small{ \ a\gt1 \ }\)のとき\(\small{ \ x\leqq p \ }\)
(ii)\(\small{ \ 0\lt a\lt 1 \ }\)のとき\(\small{ \ x\geqq p \ }\)
②\(\small{ \ 2^{2x}+2^{x+1}-3\geqq0 \ }\)
\(\small{ \ 2^x=t \ }\)として
\(\small{ \ t^2+2t-3\geqq 0 \ }\)を解く
③\(\small{ \ 4^{x}+4^{-x}+2^x+2^{-x}\lt0 \ }\)
\(\small{ \ 2^x+2^{-x}=t \ }\)として
\(\small{ \ t^2+t-2\lt0 \ }\)を解く
指数を含む不等式の基本
最初に言ったけど指数関数を含む不等式はまず\(\small{ \ 2^x\geqq8 \ }\)を求めて、そこから\(\small{ \ 2^x\geqq2^3 \ }\)に変形して底\(\small{ \ 2\gt1 \ }\)より\(\small{ \ x\geqq3 \ }\)って求めるのが基本なんだ。

だからまずは\(\small{ \ a^x\geqq p \ }\)の形にすることが大切なんだ。この\(\small{ \ a^x\geqq p \ }\)の形を常に解けるようにしよう。
次の不等式を解け。
(1)\(\small{ \ 2^x\leqq 4^{x-2} \ }\)
(2)\(\small{ \ (0.2)^{2x-1}\geqq\displaystyle\frac{1}{\sqrt[3]{25}} \ }\)
(3)\(\small{ \ 2^x\geqq 3 \ }\)
(4)\(\small{ \ \left(\displaystyle\frac{1}{2}\right)^x\geqq 3 \ }\)
(1)\(\small{ \ 2^x\leqq 4^{x-2} \ }\)
\(\small{ \ 2^x\leqq 2^{2(x-2)} \ }\)
\(\small{ \ x\leqq 2(x-2) \ }\)
\(\small{ \ \therefore x\geqq4 \ }\)
(2)\(\small{ \ (0.2)^{2x-1}\geqq\displaystyle\frac{1}{\sqrt[3]{25}} \ }\)
\(\small{ \ (5^{-1})^{2x-1}\geqq 5^{-\frac{2}{3}} \ }\)
\(\small{ \ 5^{-2x+1}\geqq 5^{-\frac{2}{3}} \ }\)
\(\small{ \ -2x+1 \geqq -\displaystyle\frac{2}{3} \ }\)
\(\small{ \ x \leqq \displaystyle\frac{5}{6} \ }\)
(3)\(\small{ \ 2^x\geqq3 \ }\)
\(\small{ \ \therefore x\geqq \log_23 \ }\)

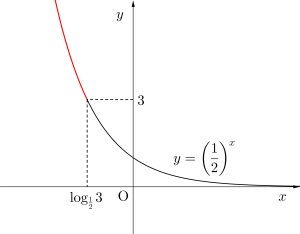
(4)\(\small{ \ \left(\displaystyle\frac{1}{2}\right)^x\geqq3 \ }\)
\(\small{ \therefore x\leqq \log_{\frac{1}{2}}3 \ }\)

\(\small{ \ 2^x\geqq3 \ }\)
底\(\small{ \ 2 \ }\)の対数をとると
\(\small{ \ \log_22^x\geqq \log_23 \ }\)
\(\small{ \ x\geqq \log_23 \ }\)
\(\small{ \ \left(\displaystyle\frac{1}{2}\right)^x\geqq3 \ }\)
底\(\small{ \ \displaystyle\frac{1}{2} \ }\)の対数をとると
\(\small{ \ \log_{\frac{1}{2}}\left(\displaystyle\frac{1}{2}\right)^x\geqq \log_{\frac{1}{2}}3 \ }\)
\(\small{ \ x\leqq \log_{\frac{1}{2}}3 \ }\)
このままでもいいけど底を変換して
\(\small{ \ \therefore x\leqq -\log_23 \ }\)
対数は底が自然数の方がどれくらいの値になのか考えやすいよね。
対数も底の大きさによって不等号の向きが変わるから注意しよう。
指数関数と二次不等式
次は指数を置換して二次不等式にする問題について考えていこう。
まずは以前書いた指数の置換について確認しておこう。
上の記事や指数関数を含む方程式の解き方と同じで置換するのは\(\small{ \ t=a^x \ }\)か\(\small{ \ t=a^x+a^{-x} \ }\)になる。
\(\small{ \ t=2^x \ }\)として\(\small{ \ t \ }\)の二次不等式になる場合、元の式には\(\small{ \ 4^x \ }\)や\(\small{ \ 2^{2x} \ }\)、\(\small{ \ \left(2^x\right)^2 \ }\)が入っているはずだからね。
\(\small{ \ t=2^x+2^{-x} \ }\)として\(\small{ \ t \ }\)の二次不等式になる場合は、元の式には\(\small{ \ 4^x+4^{-x} \ }\)や\(\small{ \ 2^{2x}+2^{-2x} \ }\)、\(\small{ \ \left(2^x\right)^2+\left(2^{-x}\right)^2 \ }\)が入っているはず。
最初に言ったように、いきなり\(\small{ \ x\geqq3 \ }\)を求めるんじゃなくて\(\small{ \ 2^x\geqq 8 \ }\)を求めたいわけだから、どの文字を置けばいいか考えて問題を解こう。
次の不等式を解け。
(1)\(\small{ \ 4^x+2^{x+1}-3\leqq0 \ }\)
(2)\(\small{ \ 9^x+9^{-x}-3^x-3^{-x}\leqq4 \ }\)
(1)\(\small{ \ 4^x+2^{x+1}-3\leqq0 \ }\)
\(\small{ \ t=2^x \ }\)とおく(\(\small{ \ t\gt0 \ }\))
\(\small{ \ t^2+2t-3\leqq0 \ }\)
\(\small{ \ (t+3)(t-1)\leqq0 \ }\)
\(\small{ \ t\gt0 \ }\)より\(\small{ \ 0\lt t \leqq 1 \ }\)
\(\small{ \ 0\lt 2^x\leqq1 \ }\)より\(\small{ \ x\leqq0 \ }\)
(2)\(\small{ \ 9^x+9^{-x}-3^x-3^{-x}-4\leqq0 \ }\)
\(\small{ \ t=3^x+3^{-x} \ }\)とおく(\(\small{ \ t\geqq2 \ }\))
\(\small{ \ t^2-t-6\leqq0 \ }\)
\(\small{ \ (t+2)(t-3)\leqq0 \ }\)
\(\small{ \ t\geqq2 \ }\)より\(\small{ \ 2\leqq t\leqq3 \ }\)
\(\small{ \ a=3^x \ }\)とおくと(\(\small{ \ a\gt0 \ }\))
すべての実数\(\small{ \ x \ }\)で\(\small{ \ t\geqq2 \ }\)を満たすので
\(\small{ \ a+\displaystyle\frac{1}{a}\leqq 3 \ }\)を考えればよい
\(\small{ \ a^2+1\leqq3a \ }\)
\(\small{ \ a^2-3a+1\leqq0 \ }\)
\(\small{ \ \displaystyle\frac{3-\sqrt{5}}{2}\leqq a \leqq \displaystyle\frac{3+\sqrt{5}}{2} \ }\)
\(\small{ \ \displaystyle\frac{3-\sqrt{5}}{2}\leqq 3^x \leqq \displaystyle\frac{3+\sqrt{5}}{2} \ }\)
\(\small{ \ \therefore \log_3\displaystyle\frac{3-\sqrt{5}}{2}\leqq x \leqq \log_3\displaystyle\frac{3+\sqrt{5}}{2} \ }\)

\(\small{ \ 0\lt a^x\lt a^2 \ }\)を\(\small{ \ 1\lt x \lt2 \ }\)って書く人たまに見かけるからね。これは間違い。\(\small{ \ 0\lt a^x\lt a^2 \ }\)は\(\small{ \ x\lt2 \ }\)だから注意しよう。
Point 指数関数を含む不等式の解き方
①置換して二次不等式へ変換する
②置換した文字の範囲を考える
\(\small{ \ a\gt0 \ (a\neq1) \ }\)のとき
\(\small{ \ a^{2x}-a^{x+2}-a^{-x-2}+1\leqq0 \ }\)を解け
\(\small{ \ a^{2x}-a^{x+2}-a^{x-2}+1\leqq0 \ }\)
\(\small{ \ a^{2x}-a^2a^{x}-\displaystyle\frac{1}{a^2}a^{x}+1\leqq0 \ }\)
\(\small{ \ a^{2x}-\left(a^2+\displaystyle\frac{1}{a^2}\right)a^{x}+1\leqq0 \ }\)
\(\small{ \ a^x=t \ }\)とすると
\(\small{ \ t^{2}-\left(a^2+\displaystyle\frac{1}{a^2}\right)t+1\leqq0 \ }\)
\(\small{ \ t^{2}-\left(a^2+\displaystyle\frac{1}{a^2}\right)t+1\leqq0 \ }\)
\(\small{ \ \left(t-a^2\right)\left(t-\displaystyle\frac{1}{a^2}\right)\leqq0 \ }\)
(i)\(\small{ \ a\gt1 \ }\)のとき
\(\small{ \ \displaystyle\frac{1}{a^2}\leqq t \leqq a^2 \ }\)
\(\small{ \ \displaystyle\frac{1}{a^2}\leqq a^x \leqq a^2 \ }\)
\(\small{ \ -2 \leqq x \leqq 2 \ }\)(\(\small{ \ \because \ a\gt1 \ }\))
(ii)\(\small{ \ 0\lt a \lt 1 \ }\)のとき
\(\small{ \ a^2\leqq t \leqq\displaystyle\frac{1}{a^2} \ }\)
\(\small{ \ a^2\leqq a^x \leqq\displaystyle\frac{1}{a^2} \ }\)
\(\small{ \ -2 \leqq x \leqq 2 \ }\)(\(\small{ \ \because \ 0\lt a \lt1 \ }\))
(I)(ii)より\(\small{ \ -2 \leqq x \leqq 2 \ }\)


