こんにちは、リンス(@Lins016)です。
今回はカルノー図とベン図について学習していこう。
カルノー図とは
論理式を簡単に示すための図で、モーリス・カルノーが発明した図だから、その名前をとってカルノー図って呼ばれているんだ。
これを論理式ではなくて、高校数学の確率に利用してみようっていうのが今回の記事になる。どうしてカルノー図を利用するかというと、このあと学習する条件付き確率を考えるときにベン図より視覚的に見やすいから。
学校の先生でも条件付き確率のときにカルノー図を利用する先生も割と多いと思う。
絶対に使わないと解けないなんてことはないから、必ず使う必要はないんだけど、そんなに難しくもないから、この記事を読んで使えるようになろう。
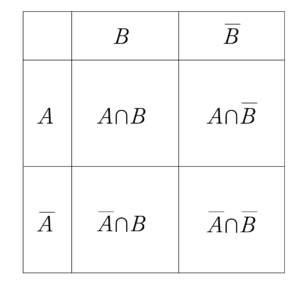
\(\small{ \ 2 \ }\)つの事象のとき
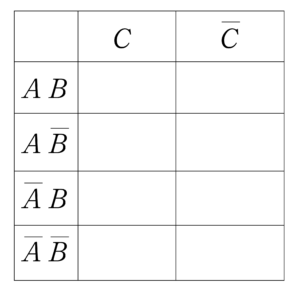
\(\small{ \ 3 \ }\)つの事象のとき
ベン図とカルノー図
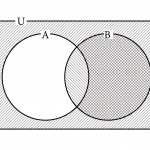
高校数学の教科書にはベン図が使われている。ベン図については下の記事で確認しておこう。 和集合や共通部分のベン図を利用した考え方について詳しく解説しています。 続きを見る
ベン図の書き方
\(\small{ \ 2 \ }\)つの集合\(\small{ \ A \ }\)と\(\small{ \ B \ }\)があるとき、その部分集合は「集合\(\small{ \ A \ }\)に含まれているか含まれていないか」「集合\(\small{ \ B \ }\)に含まれているか含まれていないか」に分けられるよね。
つまり\(\small{ \ A \cap B \ }\)、\(\small{ \ A \cap \overline{B} \ }\)、\(\small{ \ \overline{A} \cap B \ }\)、\(\small{ \ \overline{A} \cap \overline{B} \ }\)の\(\small{ \ 4 \ }\)つに分けられる。
これをベン図とカルノー図で書くとそれぞれ下のようになる。どっちが見やすいかな?
ベン図
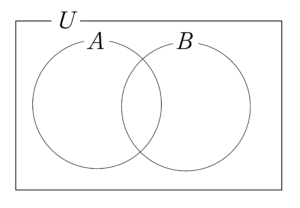
カルノー図

人それぞれで、どっちも大差ないって言う人もいるかと思うけど、条件付き確率を考えるときはカルノー図の方が使いやすかったりするんだ。
条件付き確率の求める答えは\(\small{ \ P_A(B)=\displaystyle\frac{P(A\cap B)}{P(A)}=\displaystyle\frac{n(A\cap B)}{n(A)} \ }\)になるから必要な部分がわかりやすくなるってこともあるし、数値を書き込んだときカルノー図は見やすいってこともある。
カルノー図を書いてみよう
それじゃ次にカルノー図を書いてみて、視覚的にわかりやすいか確認してみよう。
教科書にあるような次の問題のカルノー図を書いてみよう。
\(\small{ \ 60 \ }\)人の生徒に数学マークと数学記述の試験を行った。数学マークの合格者は\(\small{ \ 50 \ }\)人、数学記述の合格者は\(\small{ \ 30 \ }\)人、\(\small{ \ 2 \ }\)つとも不合格であった者は\(\small{ \ 8 \ }\)人であった。
(1)\(\small{ \ 2 \ }\)つとも合格した者は何人か。
(2)数学マークだけ合格した者は何人か。
(3)数学記述だけ合格した者は何人か。
ベン図を利用して(特に利用しなくても解けるけど、視覚的にあったほうがいいよね)解くと
\(\small{ \ n(U)=60 \ }\)
\(\small{ \ n(A)=50 \ }\) (\(\small{ \ A \ }\)は数学マーク)
\(\small{ \ n(B)=30 \ }\) (\(\small{ \ B \ }\)は数学記述)
\(\small{ \ n(\overline{A}\cap \overline{B})=8 \ }\)
\(\small{ \ n(\overline{A}\cap \overline{B})=n(\overline{A\cup B}) \ }\)
\(\small{\begin{eqnarray} \ \!n(A\cap B)&=&n(U)-n(\overline{A\cup B})\\[3pt]
&=&n(\overline{A\cup B})=42 \ \end{eqnarray}}\)
\(\small{ \ n(A\cap B)=n(A)+n(B)-n(A\cap B) \ }\)
\(\small{ \ n(A\cap B)=50+30-52=28 \ }\)
\(\small{ \ n(A\cap \overline{B})=n(A)-n(A\cap B)=50-28=22 \ }\)
\(\small{ \ n(\overline{A}\cap B)=n(B)-n(A\cap B)=30-28=2 \ }\)

これをカルノー図を利用すると次のようになるんだ。
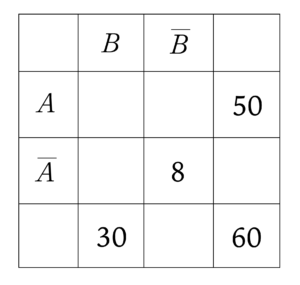
まずはわかっている情報を書き込もう。
一番右と一番下には合計の欄を作ると
\(\small{ \ n(U)=60 \ }\)
\(\small{ \ n(A)=50 \ }\)
\(\small{ \ n(B)=30 \ }\)
\(\small{ \ n(\overline{A}\cap \overline{B})=8 \ }\)
は次のように書き込める。
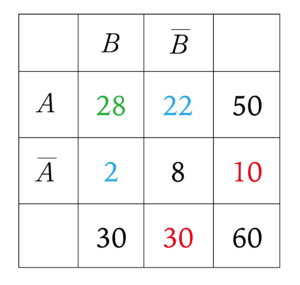
まずは全体が\(\small{ \ 60 \ }\)になるから一番右と一番下の赤い字の部分がすぐわかる。
赤字の部分がわかったら、\(\small{ \ \overline{A} \ }\)と\(\small{ \ \overline{B} \ }\)の合計から青字の部分がわかる。
そして最後に\(\small{ \ A \ }\)または\(\small{ \ B \ }\)の合計から緑字の部分がわかる。
暗算で簡単に求めることができるよね。
ただ、残った部分が簡単にわかるから便利ってだけじゃないんだ。
このあと学習する条件付き確率は\(\small{ \ P_A(B)= \displaystyle\frac{P(A\cap B)}{P(A)} \ }\)を計算するんだけど、このときベン図より視覚的にわかりやすいっていうのもあって、カルノー図が使われてる。
例えば、いまの問題を確率の問題に変えた場合、
\(\small{ \ 60 \ }\)人の生徒に数学マークと数学記述の試験を行った。数学マークの合格者は\(\small{ \ 50 \ }\)人、数学記述の合格者は\(\small{ \ 30 \ }\)人、\(\small{ \ 2 \ }\)つとも不合格であった者は\(\small{ \ 8 \ }\)人であった。この中\(\small{ \ 60 \ }\)人の中から無作為に\(\small{ \ 1 \ }\)人を選ぶ確率を考える。選ばれた\(\small{ \ 1 \ }\)人が数学マークの合格者のとき、その人が数学記述の合格者である確率を求めよ。
この問題の場合求める確率は、
カルノー図があると視覚的に簡単だよね。このあたりについては条件付き確率の記事で問題と一緒に紹介してるから、そっちの記事を読んでほしい。 条件付き確率の考え方や問題文の読み取り、カルノー図の利用について詳しく解説しています。 続きを見る

条件付き確率
3つの集合のベン図とカルノー図
それじゃ\(\small{ \ 3 \ }\)つの集合\(\small{ \ A,B,C \ }\)の場合、どんなベン図やカルノー図になるか確認しておこう。
集合\(\small{ \ A \ }\)に属する・属しない、集合\(\small{ \ B \ }\)に属する・属しない、集合\(\small{ \ C \ }\)に属する・属しないの\(\small{ \ 2 \times 2 \times 2=8 \ }\)の集合に分かれるから次のように書くんだ。
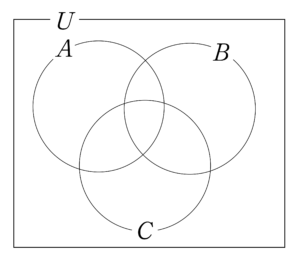

4つの集合のベン図とカルノー図
\(\small{ \ 4 \ }\)つの集合\(\small{ \ A,B,C,D \ }\)になると全部で\(\small{ \ 16 \ }\)通りの部分集合になるから、ベン図を書くのはすごく大変なる。\(\small{ \ 4 \ }\)つの円を書けばいいかなって思うけど、実際間違っている図だと\(\small{ \ 14 \ }\)箇所にしか分かれてない。\(\small{ \ 16 \ }\)箇所に分かれてないといけないからね。
間違っている4つの集合のベン図
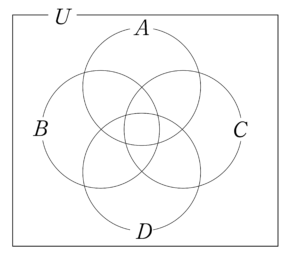
正しい集合のベン図
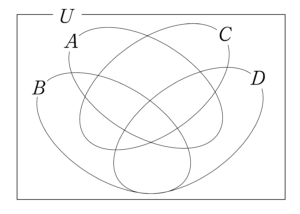
でもこれをカルノー図だったら簡単に書ける。\(\small{ \ 16 \ }\)マスあればいいから\(\small{ \ 4\times4 \ }\)のマスを作ればいいって考えると簡単だよね。
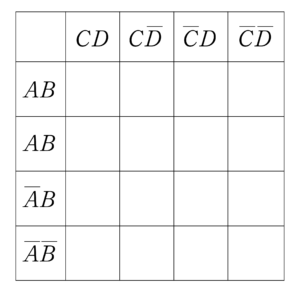
今回は特に例題とかないけど、カルノー図について理解できたかな。
カルノー図は教科書には載ってないし、絶対覚えておかないといけないってことはないんだけど、使ってみると便利だからこの際覚えて使えるようにしておこう!

