こんにちは、リンス(@Lins016)です。
今回は軌跡の方程式の基本について学習していこう。
軌跡の基本ルールを確認
軌跡の問題は、求める軌跡の点の座標を\(\small{ \ (x, \ y) \ }\)に設定しよう。
軌跡の問題は色々な形があるけど、どの形も求める軌跡の点の座標を\(\small{ \ (x, \ y) \ }\)に設定して、\(\small{ \ x, \ y \ }\)の関係式を作るっていうのが軌跡の問題の解き方になるからね。
ただ、例外として問題文が求める軌跡の座標を\(\small \ {(a, \ b) \ }\)や\(\small{ \ (X, \ Y) \ }\)と指定している場合があるから、その場合はその指示に従うようにしよう。
軌跡の問題の解き方
①求める軌跡の点の座標を\(\small{ \ (x, \ y) \ }\)に設定。
②\(\small{ \ x, \ y \ }\)の関係式をたてる。
条件を満たす座標を\(\small{ \ (x, \ y) \ }\)って設定したら、最終目的は\(\small{ \ x, \ y \ }\)の関係式を導くってことになるから、そこに向かって解答していこう。
軌跡の形を考えよう
求める軌跡の形は、基本的に今まで学習した図が書ける形になる。
文系やまだ数学Ⅲを教わっていない場合求める軌跡は、
・\(\small{ax+by+c=0 \ }\)の直線
・\(\small{y=ax^2+bx+c \ }\)の放物線
・\(\small{(x-a)^2+(y-b)^2=r^2 \ }\)の円
の答えになるから、求めた関係式がどの形に変形できるか考えながら解こう。
理系で数学Ⅲを教わっている場合は、上の三つに加えて、
・\(\small{y^2=4px \ }\)の直線
・\(\small{\displaystyle \frac{(x-p)^2}{a^2}+\frac{(y-q)^2}{b^2}=1 \ }\)の楕円
・\(\small{\displaystyle \frac{(x-p)^2}{a^2}-\frac{(y-q)^2}{b^2}=1 \ }\)の双曲線
も答えになる。
条件式の\(\small{ \ x, \ y \ }\)の係数を確認して、どの形の軌跡になるか考えていこう。
点Pの満たす条件から式を立て、\(\small{x,y}\)の軌跡を導く
今回学習する軌跡は、ある点が与えられた条件を満たすときの軌跡になる。
この条件が文章や式で与えられた問題だ。文章だけの場合、まずは式に変形するところから始めよう。
しかも式と言っても\(\small{ \ x, \ y \ }\)を含んだ形の式をたてる前に、\(\small{\mathrm{AP} \ }\)などの長さを表す文字を利用した式をたてるところから始めてみよう。
そうすると式があらかじめ示されている問題と同じ解き方になる。
簡単なところで言うと円の方程式も軌跡の考え方で求めることができる。円の中心\(\small{ \ \mathrm{Q}(a, \ b) \ }\)と円周上の点\(\small{ \ \mathrm{P}(x, \ y) \ }\)の距離が\(\small{ \ r \ }\)っていう式を立てると、\(\small{ \ \mathrm{PQ}=r \ }\)になって円の方程式が導けるんだ。
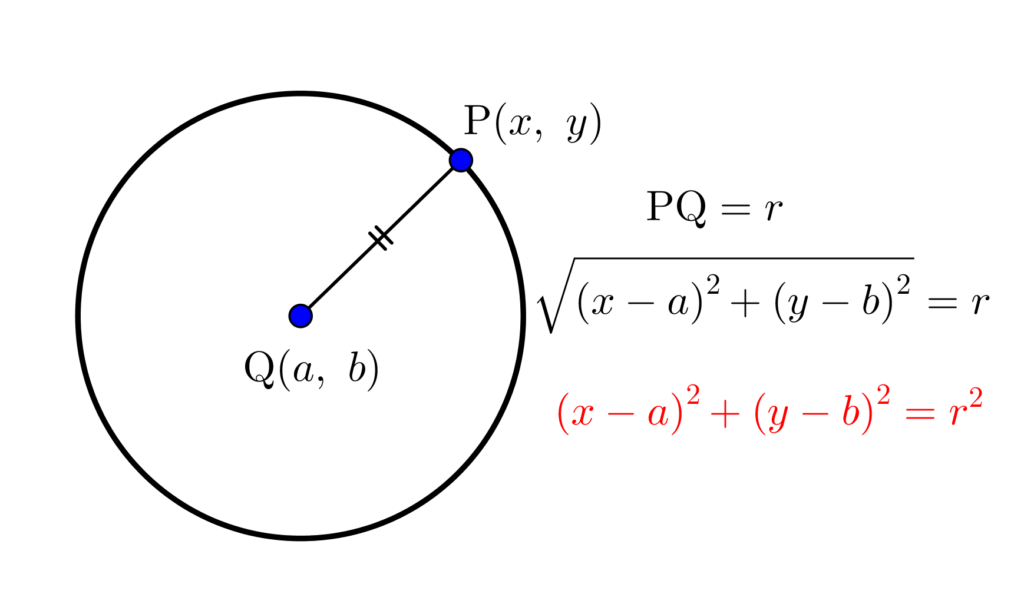
次の条件を満たす点\(\small{ \ \mathrm{P} \ }\)の軌跡の方程式を求めなさい。
(1)\(\small{\mathrm{A(-2,0)、B(3,0)}}\)からの距離が\(\small{ \ 2:3 \ }\)になる点\(\small{ \ \mathrm{P} \ }\)の軌跡
(2)\(\small{\mathrm{O(0, \ 0)、A(3, \ 0)、B(0, \ 3) \ }}\)のとき、\(\small{\mathrm{OP^2+AP^2+BP^2=15 \ }}\)を満たす点\(\small{ \ \mathrm{P} \ }\)の軌跡
(1)点\(\small{ \ \mathrm{P} \ }\)の座標を\(\small{ \ (x,y) \ }\)とおく。
\(\small{\mathrm{AP:BP=2:3}}\)
\(\small{\mathrm{3AP=2BP}}\)
両辺を二乗して
\(\small{\mathrm{9AP^2=4BP^2}}\)
\(\small{9\{(x+2)^2+y^2\}=4\{(x-3)^2+y^2\}}\)
\(\small{5x^2+60x+5y^2=0}\)
\(\small{x^2+12x+y^2=0}\)
\(\small{\therefore \left(x+6\right)^2+y^2=36}\)

(2)点\(\small{\mathrm{P}}\)の座標を\(\small{(x,y)}\)とおく
\(\small{\mathrm{OP}^2=x^2+y^2}\)
\(\small{\mathrm{AP}^2=(x-3)^2+y^2}\)
\(\small{\mathrm{BP}^2=x^2+(y-3)^2}\)
\(\small{\mathrm{OP^2+AP^2+BP^2=15} \ }\)より
\(\small{3x^2-6x+3y^2-6y+3=0}\)
\(\small{x^2-2x+y^2-2y+1=0}\)
\(\small{\therefore (x-1)^2+(y-1)^2=1}\)


そうすると(1)も(2)と同じ問題になるから、そこから辺の長さを座標で表して、軌跡を求めよう。
Point 軌跡の方程式(基本)
①点\(\small{ \ \mathrm{P} \ }\)の満たす条件から式を立て、\(\small{ \ x,y \ }\)の軌跡を導こう
一辺の長さが\(\small{ \ 2s \ }\)である正三角形\(\small{ \ \mathrm{ABC} \ }\)の\(\small{ \ 3 \ }\)つの頂点を\(\small{ \ \mathrm{A}(-s, \ 0) \ }\)、\(\small{ \ \mathrm{B}(s, \ 0) \ }\)、\(\small{ \ \mathrm{C}(0, \ \sqrt{3}s) \ }\)とする。\(\small{ \ \mathrm{AP}^2+\mathrm{BP}^2+\mathrm{CP}^2=t \ }\)であるような点\(\small{ \ \mathrm{P} \ }\)について以下の問いに答えよ。
(1)このような点\(\small{ \ \mathrm{P} \ }\)が存在するための\(\small{ \ s \ }\)、\(\small{t \ }\)についての必要十分条件と、この条件の下での点\(\small{ \ \mathrm{P} \ }\)の軌跡の方程式を求めよ。
(2) 点\(\small{ \ \mathrm{P} \ }\)の軌跡が点\(\small{ \ \mathrm{A} \ }\)を通る場合の\(\small{ \ s \ }\)と\(\small{ \ t \ }\)の関係式を求めよ。またこのときの点\(\small{ \ \mathrm{P} \ }\)の軌跡を\(\small{ \ \triangle \mathrm{ABC} \ }\)とともに図示せよ。
(1)点\(\small{ \ \mathrm{P} \ }\)の座標を\(\small{ \ (x, \ y) \ }\)とおくと、
\(\small{ \ \mathrm{AP}^2+\mathrm{BP}^2+\mathrm{CP}^2 \ }\)
\(\small{ \ =3x^2+3y^2-2\sqrt{3}sy+5t^2=t \ }\)
これを整理して
\(\small{ \ x^2+\left(y-\displaystyle \frac{\sqrt{3}}{3}s\right)^2=\displaystyle \frac{t-4s^2}{3} \ }\)
これは右辺\(\small{ \ =0 \ }\)のとき点、右辺\(\small{\gt0 \ }\)のとき円を表す。
よって求める条件は
\(\small{ \ \displaystyle \frac{t-4s^2}{3} \geqq 0 \ }\)
\(\small{ \ \therefore t \geqq 4s^2 \ }\)
このとき点\(\small{ \ \mathrm{P} \ }\)の軌跡は
\(\small{ \ t=4s^2 \ }\)のとき点\(\small{ \ \left(0, \ \displaystyle \frac{\sqrt{3}}{3}s\right) \ }\)
\(\small{ \ t \gt 4s^2 \ }\)のとき点\(\small{ \ \left(0, \ \displaystyle \frac{\sqrt{3}}{3}s\right) \ }\)を中心とする半径\(\small{ \ \sqrt{\displaystyle \frac{t-4s^2}{3}} \ }\)の円
(2)\(\small{ \ \mathrm{A}(-s, \ 0) \ }\)を(1)で求めた式に代入すると
\(\small{ \ s^2+\displaystyle \frac{s^2}{3}=\displaystyle \frac{t-4s^2}{3} \ }\)
\(\small{ \ \therefore t=8t^2 \ }\)
このとき\(\small{ \ s \gt 0 \ }\)に注意すると
\(\small{ \ \sqrt{\displaystyle \frac{8t^2-4s^2}{3}}=\displaystyle \frac{2\sqrt{3}}{3}s \ }\)になるから
点\(\small{ \ \mathrm{P} \ }\)の軌跡は
\(\small{ \ \left(0, \ \displaystyle \frac{\sqrt{3}}{3}s\right) \ }\)を中心とする半径\(\small{ \ \displaystyle \frac{2\sqrt{3}}{3}s \ }\)の円である。

