こんにちは、リンス(@Lins016)です。
今回は空間ベクトルの基本について学習していこう。
空間ベクトルの考え方
ベクトルとは大きさと向きを持つもので、高校数学では記号で書くと\(\small{ \ \vec{a} \ }\)や\(\small{ \ \overrightarrow{ \mathrm{OA} } \ }\)って書くんだったよね。
これは平面ベクトルの学習のときやったよね。
平面ベクトルだと\(\small{ \ xy \ }\)平面の成分表示で、 \(\small{ \ (a_1, \ a_2) \ }\)って書いてたけど、空間ベクトルだと\(\small{ \ x \ }\)軸、\(\small{ \ y \ }\)軸、\(\small{ \ z \ }\)軸の成分表示になるから\(\small{ \ (a_1, \ a_2, \ a_3) \ }\)のように三つの成分になるんだ。
つまり計算量が平面のときより増えるってこと。
しかも空間の図形って描きにくいから空間ベクトルは苦手って人も結構いると思うけど、平面より少し計算量が増えただけだから、平面ベクトルをきちんと理解しておくことが空間ベクトルをスムーズに学習できるポイントになるから、平面ベクトルが不安な人はまず平面ベクトルからしっかりとマスターしよう。
空間ベクトルは三つの基準のベクトルで表す
\(\small{ \ \overrightarrow{\mathrm{OP}}=s\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}}+u\overrightarrow{\mathrm{OC}} \ }\)
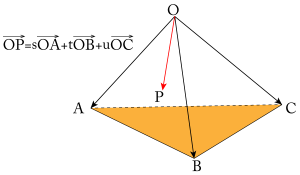
空間ベクトルと三つの基準のベクトル
\(\small{ \ \mathrm{O, \ A, \ B, \ C} \ }\)が同一平面上にないとき、空間中の全てのベクトルは適当な係数\(\small{ \ s, \ t, \ u \ }\)を用いて\(\small{ \ \overrightarrow{\mathrm{OP}}=s\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}}+u\overrightarrow{\mathrm{OC}} \ }\)って表すことができる。
しかもこの表し方はただ\(\small{ \ 1 \ }\)通りしかないんだ。まずはこのことを確実に抑えておこう。
ちなみに平面ベクトルの場合、基準のベクトルを\(\small{ \ \overrightarrow{\mathrm{OA}} \ }\)と\(\small{ \ \overrightarrow{\mathrm{OB}} \ }\)とすると、\(\small{ \ \overrightarrow{\mathrm{OP}}=s\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}} \ }\)のように二つの基準のベクトルで表すのが基本だったよね。
空間の場合は\(\small{ \ \overrightarrow{\mathrm{OP}}=s\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}}+u\overrightarrow{\mathrm{OC}} \ }\)のように基準のベクトルを三つにして表すのが基本になるんだ。
だから平面ベクトルよりも計算量が増えて大変だよね。
でも落ち着いて考えてほしい。
確かに計算量は増えるけど、することは対して変わらないんだ。
内積や成分の計算も平面で学習したときと同じように考えることもできるし、位置を表す内分や外分のベクトルも同じように考えることが出来るからね。
計算が大変になるけど、丁寧に計算していけば、別に難しい計算でもないしね。
空間ベクトルが苦手や嫌いなみんなは、解き方と計算方法をしっかりと勉強して得意分野にしていこう。
基準のベクトルの考え方
どうして基準のベクトルが三つになるのか考えてみよう。
ある点\(\small{ \ \mathrm{P} \ }\)を三つの基準のベクトル\(\small{ \ \overrightarrow{\mathrm{OA}} \ }\)と\(\small{ \ \overrightarrow{\mathrm{OB}} \ }\)と\(\small{ \ \overrightarrow{\mathrm{OC}} \ }\)を使って
\(\small{ \ \overrightarrow{\mathrm{OP}}=s\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}}+u\overrightarrow{\mathrm{OC}} \ }\)って表すことができるとする。
この前半部分の\(\small{ \ s\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}} \ }\)について考えてみよう。
これは\(\small{ \ \mathrm{O, \ A, \ B} \ }\)で作られる平面\(\small{ \ \mathrm{OAB} \ }\)上にあるベクトルになるよね。
\(\small{ \ \overrightarrow{\mathrm{OD}}=s\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}} \ }\)とすると
\(\small{ \ s, \ t \ }\)に任意の数字を入れることで、\(\small{ \ \mathrm{D} \ }\)は平面\(\small{ \ \mathrm{OAB} \ }\)上の任意の位置にあると言えるよね。
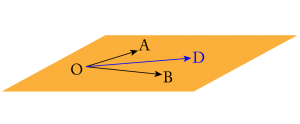
この部分は平面ベクトルの基本の考え方にもなっているから、「?」って思った人はもう一度平面ベクトルの基本を読んでおこう。
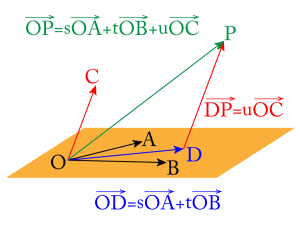
この平面\(\small{ \ \mathrm{OAB} \ }\)上にない点\(\small{ \ \mathrm{C} \ }\)の\(\small{ \ \overrightarrow{\mathrm{OC}} \ }\)を\(\small{ \ u \ }\)倍することで\(\small{ \ \overrightarrow{\mathrm{OP}}=\overrightarrow{\mathrm{OD}}+u\overrightarrow{\mathrm{OC}} \ }\)が言えるよね。
つまり\(\small{ \ s, \ t, \ u \ }\)に数値を代入することで\(\small{ \ \overrightarrow{\mathrm{OP}}=s\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}}+u\overrightarrow{\mathrm{OC}} \ }\)は全ての空間上の点のベクトルを表すことができるんだ。
ベクトルは始点を揃えよう
ベクトルを解く上で大事なことは「始点を揃える」こと。
始点って言うのはベクトルが始まる位置で、それに対してベクトルが終わる位置(矢印の先)を終点っていうからね。
\(\small{ \ \overrightarrow{ \mathrm{AB} } \ }\)、\(\small{ \ \overrightarrow{ \mathrm{BC} } \ }\)、\(\small{ \ \overrightarrow{ \mathrm{OA} } \ }\)って始点がバラバラだよね。こうなっているとベクトルは扱いにくいんだ。
平面ベクトルでも学習したけど空間ベクトルでも同じで、始点は必ず揃えよう。
図のように点\(\small{ \ \mathrm{O} \ }\)から点\(\small{ \ \mathrm{A} \ }\)を見ると右向きだけど、点\(\small{ \ \mathrm{B} \ }\)から\(\small{ \ \mathrm{A} \ }\)を見ると左向きだよね。
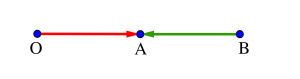
同じ点を見てるのに始点が違うと右向きだったり左向きだったりして向きが変わるし、さらに大きさも変わってくる。
だから始点がバラバラなベクトルはホント扱いにくいんだ。
基準となる始点から見てどの向きにどれくらいの大きさって統一してあったほうが絶対わかりやすいから、常に始点を揃えることが大切になるんだ。
始点の揃え方は\(\small{ \ \overrightarrow{\mathrm{MN}}=\overrightarrow{\mathrm{ON}}-\overrightarrow{\mathrm{OM}} \ }\)のようにすることで始点を変更することができる。
ベクトルの和から\(\small{ \ \overrightarrow{\mathrm{ON}}=\overrightarrow{\mathrm{OM}}+ \overrightarrow{\mathrm{MN}} \ }\)がいえるから、これを移項することで\(\small{ \ \overrightarrow{\mathrm{MN}}=\overrightarrow{\mathrm{ON}}-\overrightarrow{\mathrm{OM}} \ }\)が導けるよね。
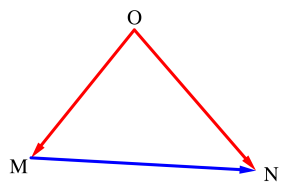
そろえたい始点の文字\(\small{ \ ■}\)(\(\small{■}\)はどんな文字でもOK)を文字の前に付けて、終点\(\small{ \ \mathrm{N} \ }\)のベクトルから始点の文字\(\small{ \ \mathrm{M} \ }\)のベクトルを引くことで始点を変更することが出来る。
\[\Large{ \ \overrightarrow{\mathrm{MN}}=\overrightarrow{■\mathrm{N}}-\overrightarrow{■\mathrm{M}} \ }\]
常にこの形で始点を変更することを覚えておこう。
これは平面ベクトルのときも言ったけど、空間ベクトルでもまったく同じだからね。必ず始点の揃った三つの基準のベクトルで、その他のベクトルも表そう。
空間図形の描き方
空間図形って書くの難しいよね。いきなりきれいに書くのは難しいけど、1つだけ約束を作っておこう。
それは奥にある線は破線にするってこと。
たったそれだけでだいぶ図がきれいになるから、常に意識しておこう。
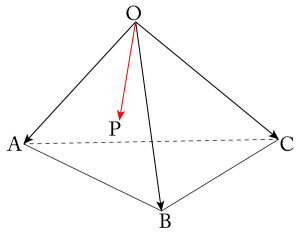
あとはなるべく二つの線が重ならないように描こう。\(\small{ \ \overrightarrow{ \mathrm{OP} } \ }\)と\(\small{ \ \overrightarrow{ \mathrm{OB} } \ }\)が重なったりすると問題が考えにくいよね。
図は必ず正確に描かなくても大丈夫。正確であるに越したことはないけど、あくまで問題を考える補助だから、正確に描くことにこだわって時間を使いすぎても意味ないからね。ある程度の図がサッとかけるようになることが重要だからね。図を描くのも練習だから、なるべく描くようにしよう。

Point 空間ベクトルの基本
①空間ベクトルは三つの基準のベクトルでその他のベクトルを表そう
②ベクトルは始点を必ず揃えよう

