空間ベクトルと直線の方程式

こんにちは、リンス(@Lins016)です。
今回は空間ベクトルと直線の方程式について学習していこう。

空間中の直線の方程式

直線の方程式って言われると $\small{ \ ax+by+c=0 \ }$ や $\small{ \ y=ax+b \ }$ って思うけど、これは $\small{ \ xy \ }$ 平面の直線の方程式だよね。
もちろん空間中でも直線の方程式ってあるんだ。これをベクトル方程式で導いてみよう。

空間ベクトルと直線の方程式

$\small{ \ \mathrm{A}(\overrightarrow{a}) \ }$ を通り、 $\small{ \ \overrightarrow{b} \ }$ に平行な直線

$\small{ \ \overrightarrow{p}=\overrightarrow{a}+t\overrightarrow{b} \ }$

$\small{ \ \overrightarrow{a}=(x_0, \ y_0, \ z_0) \ }$ 、 $\small{ \ \overrightarrow{b}=(l, \ m, \ n) \ }$ のとき
$\small{ \ \displaystyle\frac{x-x_0}{l}=\displaystyle\frac{y-y_0}{m}=\displaystyle\frac{z-z_0}{n} \ }$

直線のベクトル方程式

平面で学習したベクトル方程式と考え方は同じだから、まずは一度ベクトルを利用した平面の直線の方程式を復習しておこう。
平面は $\small{ \ x \ }$ 軸、 $\small{ \ y \ }$ 軸だけど、空間はこれに $\small{ \ z \ }$ 軸が増えるだけで、考え方は同じだからね。

▼あわせてCHECK▼(別ウィンドウで開きます)

直線のベクトル方程式

直線上の点を表すベクトルを $\small{ \ \overrightarrow{p}=(x, \ y, \ z) \ }$ 、直線が通る点を $\small{ \ \overrightarrow{a}=(x_0, \ y_0, \ z_0) \ }$ 、直線と平行なベクトルを $\small{ \ \overrightarrow{b}=(l, \ m, \ n) \ }$ とすると媒介変数 $\small{ \ t \ }$ を使って $\small{ \ \overrightarrow{p}=\overrightarrow{a}+t\overrightarrow{b} \ }$ になるよね。
空間でも平面の時と同じ式使うからね。

これを成分表示で書くと、
$\small{ \ \overrightarrow{p}=\overrightarrow{a}+t\overrightarrow{b} \ }$
$\small{\begin{eqnarray} \ (x, \ y, \ z)&=&(x_0, \ y_0, \ z_0)+t(l, \ m, \ n)\\ &=&(x_0+tl, \ y_0+tm, \ z_0+tn) \ \end{eqnarray}}$

$\small{ \ \begin{eqnarray} \left\{ \begin{array}{l} x=x_0+tl\\ y=y_0+tm\\ z=z_0+tn \end{array} \right. \end{eqnarray} \ }$

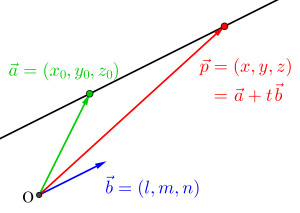
$\small{ \ t \ }$ に色々な値を代入すると直線上の点を表すからね。

だからこの $\small{ \ \overrightarrow{p}=\overrightarrow{a}+t\overrightarrow{b} \ }$ が直線を表すベクトル方程式になるんだ。

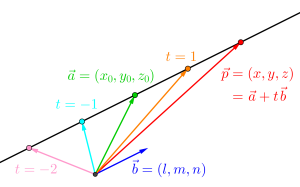
この媒介変数 $\small{ \ t \ }$ を消して、直線の方程式を導いてみよう。
これを「 $\small{ \ t= \ }$ 」の形に変形してみよう。
$\small{ \ t=\displaystyle\frac{x-x_0}{l}=\displaystyle\frac{y-y_0}{m}=\displaystyle\frac{z-z_0}{n} \ }$
つまりこの $\small{ \ t \ }$ を消去した
$\small{ \ \displaystyle\frac{x-x_0}{l}=\displaystyle\frac{y-y_0}{m}=\displaystyle\frac{z-z_0}{n} \ }$ が空間中の直線の方程式ってことになるからね。

つまりこの直線の方程式は $\small{ \ (x_0, \ y_0, \ z_0) \ }$ を通り、 $\small{ \ (l, \ m, \ n) \ }$ に平行な直線を表してるってことね。この $\small{ \ (l, \ m, \ n) \ }$ のベクトルを方向ベクトルっていうから覚えておこう。

分母が0になる場合

$\small{ \ 1 \ }$ つ注意しておきたいのがね。
例えば $\small{ \ n=0 \ }$ だと $\small{ \ \displaystyle\frac{z-z_0}{0} \ }$ ってなって分母が $\small{ \ 0 \ }$ になるから数学的にダメだよね。

$\small{ \ l, \ m, \ n \ }$ の中に $\small{ \ 0 \ }$ があった場合、ただこの $\small{ \ \displaystyle\frac{x-x_0}{l}=\displaystyle\frac{y-y_0}{m}=\displaystyle\frac{z-z_0}{n} \ }$ に代入してもだめなんだ。だからその時は、 $\small{ \ \overrightarrow{p}=\overrightarrow{a}+t\overrightarrow{b} \ }$ の式で $\small{ \ 0 \ }$ を代入しよう。

$\small{ \ n=0 \ }$ なら
$\small{\begin{eqnarray} \ (x, \ y, \ z)&=&(x_0, \ y_0, \ z_0)+t(l, \ m, \ 0)\\ &=&(x_0+tl, \ y_0+tm, \ z_0) \ \end{eqnarray}}$
になるから、求める直線の式は
$\small{ \ \displaystyle\frac{x-x_0}{l}=\displaystyle\frac{y-y_0}{m}, \ z=z_0 \ }$
になるんだ。

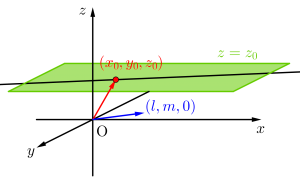
これは $\small{ \ z=z_0 \ }$ 平面上に $\small{ \ \displaystyle\frac{x-x_0}{l}=\displaystyle\frac{y-y_0}{m} \ }$ の直線があることを示しているからね。

直線上の垂線の足

ある点から直線に垂線を下ろすって問題があるけど、直線に垂線を下ろすってことは直線と垂線になる線分が垂直ってことだから、内積を利用して解こう。

このとき垂直になるのは直線の方向ベクトルと垂線のベクトルだから注意しよう。

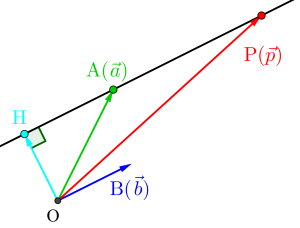
座標の分からない $\small{ \ \mathrm{OH}\perp\mathrm{AH} \ }$ を計算するよりも $\small{ \ \mathrm{OH}\perp\overrightarrow{b} \ }$ のほうが簡単だからね。

例題を確認

問題解答

(1)直線 $\small{ \ \displaystyle\frac{x-3}{2}=\displaystyle\frac{y-1}{3}=-z+2 \ }$ と平面 $\small{ \ 2x-3y+z-11=0 \ }$ との交点の座標を求めよ。

(2) $\small{ \ \mathrm{P}(1, \ 4, \ 5) \ }$ から直線 $\small{ \ \displaystyle\frac{x-3}{2}=\displaystyle\frac{y-1}{3}=-z+2 \ }$ に垂線 $\small{ \ \mathrm{PH} \ }$ を下ろす。このとき $\small{ \ \mathrm{H} \ }$ の座標を求めよ。

(1) $\small{ \ \displaystyle\frac{x-3}{2}=\displaystyle\frac{y-1}{3}=-z+2=t \ }$ とすると、
$\small{ \ \begin{eqnarray} \left\{ \begin{array}{l} x=2t+3\\ y=3t+1\\ z=-t+2 \end{array} \right. \end{eqnarray} \ }$
これを直線の方程式に代入して

$\small{ \ 2(2t+3)-3(3t+1)+(-t+2)-11=0 \ }$

$\small{ \ -6t-6=0 \ }$
$\small{ \ \therefore t=-1 \ }$
$\small{\begin{eqnarray} \ (x, \ y, \ z)&=&(2t+3, \ 3t+1, \ -t+2)\\ &=&(1, \ -2, \ 3) \ \end{eqnarray}}$

(2) $\small{ \ \displaystyle\frac{x-3}{2}=\displaystyle\frac{y-1}{3}=-z+2=t \ }$ とすると、
$\small{ \ \begin{eqnarray} \left\{ \begin{array}{l} x=2t+3\\ y=3t+1\\ z=-t+2 \end{array} \right. \end{eqnarray} \ }$
つまり直線上の点 $\small{ \ \mathrm{P}(x, \ y, \ z)=(2t+3, \ 3t+1, \ -t+2) \ }$ とおける
$\small{\begin{eqnarray} \ \overrightarrow{\mathrm{PH}}&=&(1, \ 4, \ 5)-(2t+3, \ 3t+1, \ -t+2)\\ &=&(-2t-2, \ -3t+3, \ t+3) \ \end{eqnarray}}$
また直線の方程式を変形して、
$\small{\begin{eqnarray} \ (x, \ y, \ z)&=&(2t+3, \ 3t+1, \ -t+2)\\ &=&(3, \ 1, \ 2)+t(2, \ 3, \ -1) \ \end{eqnarray}}$
直線の方向ベクトルと $\small{ \ \overrightarrow{\mathrm{PH}} \ }$ が垂直になればよい
$\small{ \ (-2t-2, \ -3t+3, \ t+3)\cdot(2, \ 3, \ -1)=0 \ }$
$\small{ \ 2(-2t-2)+3(-3t+3)-(t+3)=0 \ }$
$\small{ \ -14t+2=0 \ }$
$\small{ \ t=\displaystyle\frac{1}{7} \ }$
$\small{ \ (x, \ y, \ z)=\left(\displaystyle\frac{23}{7}, \ \displaystyle\frac{10}{7}, \ \displaystyle\frac{13}{7}\right) \ }$

空間中の直線の方程式は

$\small{ \ \mathrm{P}(x, \ y, \ z)=(2t+3, \ 3t+1, \ -t+2) \ }$ のような媒介変数を利用した形で問題に出てくることが多いけど、これを見たら

$\small{\begin{eqnarray} \ (x, \ y, \ z)&=&(2t+3, \ 3t+1, \ -t+2)\\ &=&(3, \ 1, \ 2)+t(2, \ 3, \ -1) \ \end{eqnarray}}$
に変形して方向ベクトル

$\small{ \ (2, \ 3, \ -1) \ }$ も頭に入れておこう。
つまり

$\small{ \ t \ }$ の係数が方向ベクトルになるってことだからね。

Point　空間ベクトルと直線の方程式

①空間中の直線の方程式を覚える
②直線の方程式と方向ベクトルの関係を確認する

次は入試レベルの問題にチャレンジ！

入試レベルにチャレンジ

問題解答

座標空間における次の $\small{ \ 3 \ }$ つの直線 $\small{ \ l, \ m, \ n \ }$ を考える。
$\small{ \ l \ }$ は点 $\small{ \ \mathrm{A}(1, \ 0, \ -2) \ }$ を通り、ベクトル $\small{ \ \overrightarrow{u}=(2, \ 1, \ -1) \ }$ に平行な直線である。
$\small{ \ m \ }$ は点 $\small{ \ \mathrm{B}(1, \ 2, \ 3) \ }$ を通り、ベクトル $\small{ \ \overrightarrow{v}=(1, \ -1, \ 1) \ }$ に平行な直線である。
$\small{ \ n \ }$ は点 $\small{ \ \mathrm{C}(1, \ -1, \ 0) \ }$ を通り、ベクトル $\small{ \ \overrightarrow{w}=(1, \ 2, \ 1) \ }$ に平行な直線である。
$\small{ \ \mathrm{P} \ }$ を $\small{ \ l \ }$ 上の点として、 $\small{ \ \mathrm{P} \ }$ から $\small{ \ l, \ m \ }$ へ下ろした垂線の足をそれぞれ $\small{ \ \mathrm{Q, \ R} \ }$ とする。
このとき $\small{ \ \mathrm{PQ}^2+\mathrm{PR}^2 \ }$ を最小にするような $\small{ \ \mathrm{P} \ }$ と、そのときの $\small{ \ \mathrm{PQ}^2+\mathrm{PR}^2 \ }$ を求めよ。

直線 $\small{ \ l, \ m, \ n \ }$ のベクトル方程式はそれぞれ

$\small{\begin{eqnarray} l&:&(x, \ y, \ z)&=&(1, \ 0, \ -2)+p(2, \ 1, \ 1)\\[2pt] &&&=&(1+2p, \ p, \ -2-p)\\[5pt] m&:&(x, \ y, \ z)&=&(1, \ 2, \ 3)+q(1, \ -1, \ 1)\\[2pt] &&&=&(1+q, \ 2-q, \ -3+q)\\[5pt] n&:&(x, \ y, \ z)&=&(1, \ -1, \ 0)+r(1, \ 2, \ 1)\\[2pt] &&&=&(1+r, \ -1+2r, \ r) \ \end{eqnarray}}$

つまり $\small{ \ \mathrm{P}(1+2p, \ p, \ -2-p) \ }$ 、 $\small{ \ \mathrm{Q}(1+q, \ 2-q, \ -3+q) \ }$ 、 $\small{ \ \mathrm{R}(1+r, \ -1+2r, \ r) \ }$ とおける。
これより

$\small{\begin{eqnarray} \ \overrightarrow{\mathrm{PQ}}&=&\overrightarrow{\mathrm{OQ}}-\overrightarrow{\mathrm{OP}}\\ &=&(q-2p, \ 2-q-p, \ -1+q+p) \ \end{eqnarray}}$

$\small{\begin{eqnarray} \ \overrightarrow{\mathrm{PR}}&=&\overrightarrow{\mathrm{OR}}-\overrightarrow{\mathrm{OP}}\\ &=&(r-2p, \ -1+2r-p, \ 2+r+p) \ \end{eqnarray}}$

$\small{ \ \mathrm{PQ}\perp m \ }$ から $\small{ \ \overrightarrow{\mathrm{PQ}}\cdot \overrightarrow{v}=0 \ }$

$\small{ \ (q-2p)\cdot1+(2-q-p)\cdot(-1)+(-1+q+p)\cdot1=0 \ }$

$\small{ \ 3q-3=0 \ }$ より $\small{ \ q=1 \ }$
$\small{ \ \mathrm{PR}\perp n \ }$ から $\small{ \ \overrightarrow{\mathrm{PR}}\cdot \overrightarrow{w}=0 \ }$

$\small{ \ (r-2p)\cdot1+(-1+2r-p)\cdot2+(2+r+p)\cdot1=0 \ }$

$\small{ \ -3p+6r=0 \ }$ より $\small{ \ p=2r \ }$
したがって
$\small{ \ \overrightarrow{\mathrm{PQ}}=(1-4r, \ 1-2r, \ 2r) \ }$
$\small{ \ \overrightarrow{\mathrm{PR}}=(-3r, \ -1, \ 2+3r) \ }$
となるので

$\small{\begin{eqnarray} \ \mathrm{PQ}^2+\mathrm{PR}^2&=&(1-4r)^2+(1-2r)^2+(2r)^2+(-3r)^2+(-1)^2+(2+3r)^2\\ &=&42r^2+7\geqq7 \ \end{eqnarray}}$

よって $\small{ \ r=0 \ }$ のとき最小値 $\small{ \ 7 \ }$
このとき $\small{ \ p=0 \ }$ より $\small{ \ \mathrm{P}(1, \ 0, \ -2) \ }$

空間ベクトルと直線の方程式

空間中の直線の方程式

直線のベクトル方程式

分母が0になる場合

直線上の垂線の足

Point 空間ベクトルと直線の方程式

Point　空間ベクトルと直線の方程式