こんにちは、リンス(@Lins016)です。
今回は空間ベクトルを利用した四面体の体積の求め方(基本)について学習していこう。
四面体の体積=底面積×高さ×1/3
今回学習するのは四面体の体積の求め方なんだけど、「成分表示されていない問題」の体積の求め方になる。
成分表示の問題だと平面の方程式の法線ベクトルや外積って裏技を利用したり色々な解き方があるけど、成分表示じゃない空間ベクトルの四面体の体積を求める問題の場合、基本的に次の方法しかない。
それは四面体のどれか一面を底面として、「底面の面積」と「底面に含まれない頂点から下ろした垂線の長さ(つまり高さ)」を求めて、中学のときに教わった「体積=底面積×高さ×\(\small{ \ 1/3 \ }\)」に代入するって方法ね。
面積や垂線の長さを求めるためには基準になる\(\small{ \ 3 \ }\)つのベクトルの大きさと内積がわかってないと解けないから、まずはそれを求めるところから始めよう。
四面体\(\small{ \ \mathrm{OABC} \ }\)の体積\(\small{ \ \mathrm{V} \ }\)
\(\small{ \ \mathrm{V}=\displaystyle\frac{1}{3}\times \mathrm{S}\times \vert \overrightarrow{\mathrm{OH}}\vert \ }\)

基準のベクトル
まずは基準となる\(\small{ \ 3 \ }\)つのベクトルの大きさや内積を求めよう。
例えば四面体\(\small{ \ \mathrm{OABC} \ }\)の体積を求める場合、基準のベクトルは\(\small{ \ \overrightarrow{\mathrm{OA}} \ }\)、\(\small{ \ \overrightarrow{\mathrm{OB}} \ }\)、\(\small{ \ \overrightarrow{\mathrm{OC}} \ }\)になるから、\(\small{ \ \vert\overrightarrow{\mathrm{OA}}\vert \ }\)、\(\small{ \ \vert\overrightarrow{\mathrm{OB}}\vert \ }\)、\(\small{ \ \vert\overrightarrow{\mathrm{OC}}\vert \ }\)と\(\small{ \ \overrightarrow{\mathrm{OA}}\cdot\overrightarrow{\mathrm{OB}} \ }\)、\(\small{ \ \overrightarrow{\mathrm{OA}}\cdot\overrightarrow{\mathrm{OC}} \ }\)、\(\small{ \ \overrightarrow{\mathrm{OB}}\cdot\overrightarrow{\mathrm{OC}} \ }\)の\(\small{ \ 6 \ }\)つの値が必要になる。
この部分が「?」って人は一度次の記事を読んで復習しておこう。空間ベクトルの成分表示じゃない問題では一番大切な部分だからね。
特によく出題されるのは正四面体で、一辺の長さが\(\small{ \ a \ }\)だとすると
\(\small{ \ \vert\overrightarrow{\mathrm{OA}}\vert=\vert\overrightarrow{\mathrm{OB}}\vert=\vert\overrightarrow{\mathrm{OC}}\vert=a \ }\)
になるよね。
底面積の求め方
四面体\(\small{ \ \mathrm{OABC} \ }\)の底面を\(\small{ \ \triangle\mathrm{ABC} \ }\)とすると、その面積は\(\small{ \ \mathrm{S}=\displaystyle\frac{1}{2}\sqrt{\vert\overrightarrow{\mathrm{AB}}\vert^2\vert\overrightarrow{\mathrm{AC}}\vert^2-\left(\overrightarrow{\mathrm{AB}}\cdot\overrightarrow{\mathrm{AC}}\right)^2} \ }\)
だから基準のベクトル\(\small{ \ \overrightarrow{\mathrm{OA}} \ }\)、\(\small{ \ \overrightarrow{\mathrm{OB}} \ }\)、\(\small{ \ \overrightarrow{\mathrm{OC}} \ }\)を使って、\(\small{ \ \vert\overrightarrow{\mathrm{AB}}\vert \ }\)、\(\small{ \ \vert\overrightarrow{\mathrm{AC}}\vert \ }\)、\(\small{ \ \overrightarrow{\mathrm{AB}}\cdot\overrightarrow{\mathrm{AC}} \ }\)を求めよう。

値を求めるためには\(\small{ \ \overrightarrow{\mathrm{AB}}=\overrightarrow{\mathrm{OB}}-\overrightarrow{\mathrm{OA}} \ }\)のように\(\small{ \ \mathrm{O} \ }\)から始まるベクトルに変えたらいいよね。
垂線の長さの求め方
垂線の長さを求める場合、垂線の足のベクトルを求めて垂線の長さを求めよう。
四面体\(\small{ \ \mathrm{OABC} \ }\)のとき、\(\small{ \ \mathrm{O} \ }\)から底面\(\small{ \ \triangle\mathrm{ABC} \ }\)に下ろした垂線の足\(\small{ \ \mathrm{H} \ }\)を\(\small{ \ \overrightarrow{\mathrm{OH}}=s\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}}+u\overrightarrow{\mathrm{OC}} \ }\)とすると、\(\small{ \ \mathrm{H} \ }\)は平面\(\small{ \ \mathrm{ABC} \ }\)上にあるから\(\small{ \ s+t+u=1\cdots① \ }\)が成り立つよね。
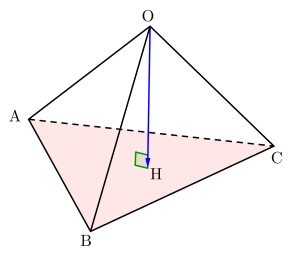
さらに\(\small{ \ \overrightarrow{\mathrm{OH}} \ }\)は平面\(\small{ \ \mathrm{ABC} \ }\)と垂直だから
\(\small{\begin{eqnarray}\overrightarrow{\mathrm{OH}}\cdot\overrightarrow{\mathrm{AB}}=0\cdots②\\
\overrightarrow{\mathrm{OH}}\cdot\overrightarrow{\mathrm{AC}}=0\cdots③ \ \end{eqnarray}}\)
が成り立つよね。
\(\small{ \ ①,②,③ \ }\)を連立することで、\(\small{ \ s, \ t, \ u \ }\)がわかって、\(\small{ \ \vert\overrightarrow{\mathrm{OH}}\vert \ }\)も求めることが出来るんだ。
体積=底面積×高さ×1/3
最後に求めた底面積と垂線の長さをかけて\(\small{ \ \displaystyle\frac{1}{3} \ }\)倍しよう。これで体積を求めることが出来る。
\(\small{ \ 1 \ }\)辺の長さが\(\small{ \ a \ }\)の正四面体\(\small{ \ \mathrm{ABCD} \ }\)の体積を求めよ。
\(\small{ \ \vert\overrightarrow{\mathrm{AB}} \vert= \vert \overrightarrow{\mathrm{AC}} \vert= \vert\overrightarrow{\mathrm{AD}} \vert=a \ }\)
\(\small{ \ \overrightarrow{\mathrm{AB}}\cdot\overrightarrow{\mathrm{AC}}=\overrightarrow{\mathrm{AB}}\cdot\overrightarrow{\mathrm{AD}}=\overrightarrow{\mathrm{AC}}\cdot\overrightarrow{\mathrm{AD}}=a^2\cos60^{\circ}=\displaystyle\frac{1}{2}a^2 \ }\)
\(\small{ \ \mathrm{A} \ }\)から平面\(\small{ \ \mathrm{BCD} \ }\)に下ろした垂線の足を\(\small{ \ \mathrm{H} \ }\)とすると、
\(\small{ \ \overrightarrow{\mathrm{AH}}=s\overrightarrow{\mathrm{AB}}+t \overrightarrow{\mathrm{AC}}+u \overrightarrow{\mathrm{AD}} \ }\)
\(\small{ \ \mathrm{H} \ }\)は平面\(\small{ \ \mathrm{BCD} \ }\)上にあるから
\(\small{ \ s+t+u=1\cdots① \ }\)
\(\small{ \ \overrightarrow{\mathrm{AH}} \ }\)は平面\(\small{ \ \mathrm{BCD} \ }\)に垂直だから
\(\small{ \ \overrightarrow{\mathrm{AH}}\cdot\overrightarrow{\mathrm{BC}}=0 \ }\)かつ\(\small{ \ \overrightarrow{\mathrm{AH}}\cdot\overrightarrow{\mathrm{BD}}=0 \ }\)
\(\small{ \ -\displaystyle\frac{1}{2}s+\displaystyle\frac{1}{2}t=0\cdots ②
\ }\)
\(\small{ \ -\displaystyle\frac{1}{2}s+\displaystyle\frac{1}{2}t=0\cdots ③ \ }\)
\(\small{ \ ①, \ ②, \ ③ \ }\)より
\(\small{ \ s=t=u=\displaystyle\frac{1}{3} \ }\)
よって
\(\small{ \ \overrightarrow{\mathrm{AH}}=\displaystyle\frac{1}{3}\left(\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{AC}}+\overrightarrow{\mathrm{AD}}\right) \ }\)
&=&\displaystyle\frac{1}{9}\left(\vert\overrightarrow{\mathrm{AB}}\vert^2+\vert\overrightarrow{\mathrm{AC}}\vert^2+\vert\overrightarrow{\mathrm{AD}}\vert^2+2 \overrightarrow{\mathrm{AB}}\cdot\overrightarrow{\mathrm{AC}}+2\overrightarrow{\mathrm{AB}}\cdot\overrightarrow{\mathrm{AD}}+2\overrightarrow{\mathrm{AC}}\cdot\overrightarrow{\mathrm{AD}}\right)\\
&=&\displaystyle\frac{2}{3}a^2 \ \end{eqnarray}}\)
\(\small{ \ \therefore \vert\overrightarrow{\mathrm{AH}}\vert=\displaystyle\frac{\sqrt{6}}{3}a \ }\)
\(\small{\begin{eqnarray} \ V&=&\displaystyle\frac{1}{3}\times \displaystyle\frac{1}{2}a^2\sin60^{\circ}\times \displaystyle\frac{\sqrt{6}}{3}a\\
&=&\displaystyle\frac{\sqrt{2}}{12}a^3 \ \end{eqnarray}}\)

計算量も減るし、計算ミスも防ぐことができるからなるべく使っていこう。
Point 四面体の体積の求め方(基本)
①基準のベクトルを設定する
②底面の面積を求める
③垂線の長さ(高さ)を求める
④体積の公式を利用する
四面体\(\small{ \ \mathrm{OABC} \ }\)の\(\small{ \ 6 \ }\)辺の長さが、\(\small{ \ \mathrm{OA}=5 \ }\)、\(\small{ \ \mathrm{OB}=\sqrt{10} \ }\)、\(\small{ \ \mathrm{OC}=3 \ }\)、\(\small{ \ \mathrm{AB}=5 \ }\)、\(\small{ \ \mathrm{AC}=3 \ }\)、\(\small{ \ \sqrt{14} \ }\)である。
\(\small{ \ \overrightarrow{\mathrm{OA}}=\overrightarrow{a} \ }\) 、\(\small{ \ \overrightarrow{\mathrm{OB}}=\overrightarrow{b} \ }\)、\(\small{ \ \overrightarrow{\mathrm{OC}}=\overrightarrow{c} \ }\)とおくとき、次の問いに答えよ。
(1)内積\(\small{ \ \overrightarrow{a}\cdot\overrightarrow{b} \ }\)、\(\small{ \ \overrightarrow{b}\cdot\overrightarrow{c} \ }\)、\(\small{ \ \overrightarrow{c}\cdot\overrightarrow{a} \ }\)を求めよ。
(2)三角形\(\small{ \ \mathrm{OAB} \ }\)の面積を求めよ。
(3)三角形\(\small{ \ \mathrm{OAB} \ }\)を含む平面上に点\(\small{ \ \mathrm{H} \ }\)がある。この平面と線分\(\small{ \ \mathrm{CH} \ }\)が垂直であるとき、\(\small{ \ \mathrm{CH} \ }\)の長さを求めよ。
(4)四面体\(\small{ \ \mathrm{OABC} \ }\)の体積を求めよ。
(1)\(\small{ \ \vert\overrightarrow{a} \vert=5 \ }\)、\(\small{ \ \vert\overrightarrow{b} \vert=\sqrt{10} \ }\)、\(\small{ \ \vert\overrightarrow{c} \vert=3 \ }\)
\(\small{ \ \vert \overrightarrow{\mathrm{AB}} \vert^2=5^2 \ }\)
\(\small{ \ \vert\overrightarrow{b}-\overrightarrow{a} \vert^2=25 \ }\)
\(\small{ \ \vert\overrightarrow{b} \vert^2-2\overrightarrow{a}\cdot\overrightarrow{b}+ \vert\overrightarrow{a} \vert^2=25 \ }\)
\(\small{ \ 10-2\overrightarrow{a}\cdot\overrightarrow{b}+25=25 \ }\)
\(\small{ \ \therefore \overrightarrow{a}\cdot\overrightarrow{b}=5 \ }\)
\(\small{ \ \vert \overrightarrow{\mathrm{BC}} \vert^2=3^2 \ }\)
\(\small{ \ \vert\overrightarrow{c}-\overrightarrow{b} \vert^2=9 \ }\)
\(\small{ \ \vert\overrightarrow{c} \vert^2-2\overrightarrow{b}\cdot\overrightarrow{c}+ \vert\overrightarrow{b} \vert^2=9 \ }\)
\(\small{ \ 9-2\overrightarrow{b}\cdot\overrightarrow{c}+10=9 \ }\)
\(\small{ \ \therefore \overrightarrow{a}\cdot\overrightarrow{b}=5 \ }\)
\(\small{ \ \vert \overrightarrow{\mathrm{AC}} \vert^2=\sqrt{14}^2 \ }\)
\(\small{ \ \vert\overrightarrow{c}-\overrightarrow{a} \vert^2=14 \ }\)
\(\small{ \ \vert\overrightarrow{c} \vert^2-2\overrightarrow{c}\cdot\overrightarrow{a}+ \vert\overrightarrow{a} \vert^2=14 \ }\)
\(\small{ \ 9-2\overrightarrow{a}\cdot\overrightarrow{b}+25=14 \ }\)
\(\small{ \ \therefore \overrightarrow{c}\cdot\overrightarrow{a}=10 \ }\)
(2)\(\small{ \ \mathrm{OAB} \ }\)の面積を\(\small{ \ \mathrm{S} \ }\)とすると
\(\small{\begin{eqnarray} \ \mathrm{S}&=&\displaystyle\frac{1}{2}\sqrt{\vert\overrightarrow{a} \vert^2 \vert\overrightarrow{b} \vert^2-\left(\overrightarrow{a}\cdot\overrightarrow{b}\right)^2}\\
&=&\displaystyle\frac{1}{2}\sqrt{5^2\times \sqrt{10}^2-5^2}\\
&=&\displaystyle\frac{15}{2} \ \end{eqnarray}}\)
(3)\(\small{ \ \mathrm{H} \ }\)は平面\(\small{ \ \mathrm{OAB} \ }\)上にあるので
\(\small{ \ \overrightarrow{\mathrm{OH}}=s\overrightarrow{a}+t\overrightarrow{b} \ }\)とおける
\(\small{ \ \overrightarrow{\mathrm{CH}}=s\overrightarrow{a}+t\overrightarrow{b}-\overrightarrow{c} \ }\)
\(\small{ \ \overrightarrow{\mathrm{CH}} \ }\)は平面\(\small{ \ \mathrm{OAB} \ }\)と垂直より
\(\small{ \ \overrightarrow{\mathrm{CH}}\cdot\overrightarrow{a}=0 \ }\)
\(\small{ \ \left(s\overrightarrow{a}+t\overrightarrow{b}-\overrightarrow{c}\right)\cdot\overrightarrow{a}=0 \ }\)
\(\small{ \ 25s+5t-10=0 \ }\)
\(\small{ \ 5s+t-2=0\cdot ① \ }\)
\(\small{ \ \overrightarrow{\mathrm{CH}}\cdot\overrightarrow{b}=0 \ }\)
\(\small{ \ \left(s\overrightarrow{a}+t\overrightarrow{b}-\overrightarrow{c}\right)\cdot\overrightarrow{b}=0 \ }\)
\(\small{ \ 5s+10t-5=0 \ }\)
\(\small{ \ s+2t-1=0\cdot ② \ }\)
\(\small{ \ ①, \ ② \ }\)より
\(\small{ \ s=\displaystyle\frac{1}{3}, \ t=\displaystyle\frac{1}{3} \ }\)
\(\small{ \ \overrightarrow{\mathrm{CH}}=\displaystyle\frac{1}{3}\overrightarrow{a}+\displaystyle\frac{1}{3}\overrightarrow{b}-\overrightarrow{c} \ }\)
&=&\displaystyle\frac{1}{9} \vert \overrightarrow{a}+\overrightarrow{b}-3\overrightarrow{c} \vert^2\\
&=&\displaystyle\frac{1}{9}\left(\vert\overrightarrow{a} \vert^2+ \vert\overrightarrow{b} \vert^2+9 \vert\overrightarrow{c} \vert^2+2\overrightarrow{a}\cdot\overrightarrow{b}-6\overrightarrow{b}\cdot\overrightarrow{c}-6\overrightarrow{c}\cdot\overrightarrow{a}\right)\\
&=&4 \ \end{eqnarray}}\)
\(\small{ \ \vert\overrightarrow{\mathrm{CH}} \vert=2 \ }\)
(4)四面体\(\small{ \ \mathrm{OABC} \ }\)の体積を\(\small{ \ \mathrm{V} \ }\)とすると
\(\small{ \begin{eqnarray}\ \mathrm{V}&=&\displaystyle\frac{1}{3}\times \mathrm{S} \times \vert \overrightarrow{\mathrm{CH}}\vert\\
&=&\displaystyle\frac{1}{3}\times \displaystyle\frac{15}{2}\times 2\\
&=&5 \ \end{eqnarray}}\)

