球面の方程式とベクトル方程式

こんにちは、リンス(@Lins016)です。
今回は球面の方程式とベクトル方程式について学習していこう。

球面の方程式

球面は球の中心から一定の距離の点の集まりだよね。これって円と同じだよね。平面図形なら円、空間図形なら球ってことになるからね。

だから一度円の方程式について復習しておこう。
円の方程式は数学Ⅱの図形と方程式と数学Bの平面ベクトルで学習したよね。

球面の方程式(標準形)

球面の方程式は、球の中心の座標とその半径が分かったら求めることが出来るよね。

球の中心の座標を\(\small{ \ (a, \ b, \ c) \ }\)、半径を\(\small{ \ r \ }\)、球面上の点を\(\small{ \ (x, \ y, \ z) \ }\)とすると球面上の点と中心の距離が半径に等しいから、\(\small{ \ \sqrt{(x-a)^2+(y-b)^2+(z-c)^2}=r \ }\)が成り立つよね。

これを二乗した
\(\small{ \ (x-a)^2+(y-b)^2+(z-c)^2=r^2 \ }\)が球面の方程式ってことになるからね。

円の方程式と同じで、右辺は\(\small{ \ r^2 \ }\)になるから右辺が\(\small{ \ 0 \ }\)以下だと球にならないから注意しよう。

球面の方程式(一般形)

次に\(\small{ \ (x-a)^2+(y-b)^2+(z-c)^2=r^2 \ }\)を展開してみよう。
\(\small{ \ x^2+y^2+z^2-2ax-2by-2cz-r^2+a^2+b^2+c^2=0 \ }\)
ここで
\(\small{ \ -2a=k, \ -2b=l, \ -2c=m, \ -r^2+a^2+b^2+c^2=n \ }\)とすると、球面の方程式は\(\small{ \ x^2+y^2+z^2+kx+ly+mz+n=0 \ }\)になるよね。
これが球面の方程式の一般形ね。

円の方程式も
\(\small{ \ \begin{eqnarray}
\left\{
\begin{array}{l}
(x-a)^2+(y-b)^2=r^2 \\
x^2+y^2+lx+my+n=0
\end{array}
\right.
\end{eqnarray} \ }\)
の\(\small{ \ 2 \ }\)つの形になってたよね。
ちなみに\(\small{ \ 2 \ }\)次関数も
\(\small{ \ \begin{eqnarray}
\left\{
\begin{array}{l}
y=a(x-p)^2+q \\
y=ax^2+bx+c
\end{array}
\right.
\end{eqnarray} \ }\)
の\(\small{ \ 2 \ }\)つの形。

大事なこと話すからきちんと覚えておいてね。
球も円も中心や半径が分かっていたほうが何かと便利だから、標準形のほうがいいよね。もちろん\(\small{ \ 2 \ }\)次関数も頂点が分かっているほうがいいから標準形がいいよね。

じゃあなぜ展開した一般形があるのかっていうと、これは円の方程式や球面の方程式、\(\small{ \ 2 \ }\)次関数の式を求めるときに、標準形より一般形でおいたほうが問題をスムーズに解けるからなんだ。

\(\small{ \ 2 \ }\)次関数の決定や円の方程式の決定で学習したけど、軸や頂点、中心や半径がまったく関係なく、ただ与えられた\(\small{ \ 3 \ }\)点を通る\(\small{ \ 2 \ }\)次関数や円の方程式を求めるとき一般形を使うんだったよね。
この場合、標準形で求めようとすると計算がホント複雑になるからね。

だから同じ考え方で、球面の方程式を求めるとき\(\small{ \ x^2+y^2+z^2+kx+ly+mz+n=0 \ }\)を使うのは球面上の\(\small{ \ 4 \ }\)点が与えられたときってことになるからね。なぜ\(\small{ \ 4 \ }\)点かっていうと\(\small{ \ k, \ l, \ m, \ n \ }\)の分からない文字\(\small{ \ 4 \ }\)つを求めるためには式が\(\small{ \ 4 \ }\)つ必要だよね。

球面上の\(\small{ \ 1 \ }\)点が与えられると、それを球面の方程式に代入して\(\small{ \ 1 \ }\)つ式ができる。
つまり\(\small{ \ k, \ l, \ m, \ n \ }\)の\(\small{ \ 4 \ }\)つの未知数を求めるためには\(\small{ \ 4 \ }\)つの点が必要になるんだ。

もちろん中心や半径が与えられていれば\(\small{ \ 4 \ }\)つも点は必要にならないけどね。

図形の方程式を決定する問題は、与えられている情報からどの形で解くか決まっているってことを確実に覚えておこう。

球面のベクトル方程式

次は球面のベクトル方程式について考えてみよう。
ベクトル方程式って言ってもそんなに難しく考える必要はなくて、球面上の\(\small{ \ (x, \ y, \ z) \ }\)の点を\(\small{ \ \overrightarrow{p} \ }\)で表せばいいだけだからね。

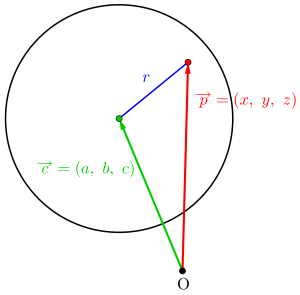
つまり中心\(\small{ \ \mathrm{C}(\overrightarrow{c}) \ }\)、半径\(\small{ \ r \ }\)とすると球面のベクトル方式は\(\small{ \ \vert\overrightarrow{p}-\overrightarrow{c}\vert=r \ }\)になるよね。
\(\small{ \ \overrightarrow{c}=(a, \ b, \ c) \ }\)とすると

\(\small{\begin{eqnarray} \ \vert\overrightarrow{p}-\overrightarrow{c}\vert&=&\vert(x, \ y, \ z)-(a, \ b, \ c)\vert\\[8pt] &=&\vert(x-a, \ y-b, \ z-c)\vert\\[8pt] &=&\sqrt{(x-a)^2+(y-b)^2+(z-c)^2} \ \end{eqnarray}}\)

になるしね。

それと球の直径に当たる\(\small{ \ 2 \ }\)点が与えられているとき、ベクトル方程式だと内積を利用して、球面の方程式を求めることもできるんだ。

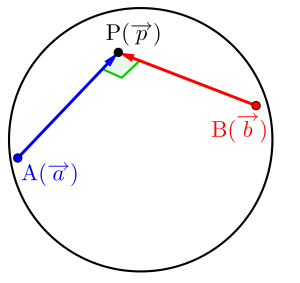
\(\small{ \ \mathrm{A}(\overrightarrow{a}) \ }\)、\(\small{ \ \mathrm{B}(\overrightarrow{b}) \ }\)を直径とすると、球面上の点\(\small{ \ \mathrm{P}(\overrightarrow{p}) \ }\)は\(\small{ \ \mathrm{AP}\perp \mathrm{BP} \ }\)になるよね。

だから\(\small{ \ \overrightarrow{\mathrm{AP}}\cdot\mathrm{\overrightarrow{BP}}=0 \ }\)が言えるんだ。
これから\(\small{ \ \left(\overrightarrow{p}-\overrightarrow{a}\right)\cdot\left(\overrightarrow{p}-\overrightarrow{b}\right)=0 \ }\)ってなるよね。

空間だとある点から一定の距離にある点の集合は球になるけど、平面だとある点から一定の距離にある点の集合は円になるよね。合わせて平面ベクトルの円のベクトル方程式も復習しておこう。

Point 球面の方程式とベクトル方程式

①球面の方程式は一般形と標準形を使い分ける
②ベクトル方程式は平面ベクトルの時と同じ考え方を利用する